Hartogs theorem
Hartogs' basic (principal, fundamental) theorem: If the function 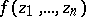 , defined in a domain
, defined in a domain 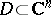 , is holomorphic at every point
, is holomorphic at every point 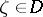 with respect to each variable
with respect to each variable 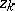 (for fixed
(for fixed 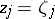 ,
, 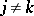 ,
, 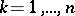 ), then it is holomorphic in
), then it is holomorphic in 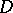 with respect to all variables. There exist many generalizations of this theorem to include cases when some of the variables are real, or when not all points of the domain
with respect to all variables. There exist many generalizations of this theorem to include cases when some of the variables are real, or when not all points of the domain 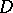 are used or when some singularities of
are used or when some singularities of 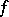 are permitted. For example: a) if a function
are permitted. For example: a) if a function 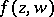 ,
, 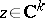 ,
, 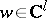 , defined in the domain
, defined in the domain  , is holomorphic in the domain
, is holomorphic in the domain  ,
, 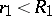 , and is holomorphic in the ball
, and is holomorphic in the ball 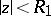 for any given
for any given 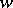 ,
, 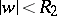 , then it is holomorphic in
, then it is holomorphic in 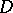 ; b) if a function
; b) if a function 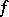 defined on
defined on 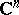 with values in the extended complex plane is rational with respect to each variable, then it is a rational function.
with values in the extended complex plane is rational with respect to each variable, then it is a rational function.
Hartogs' extension theorem: Let a domain 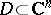 have the form
have the form 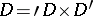 , where
, where 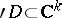 ,
, 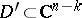 , and let
, and let 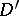 be bounded. Then any function
be bounded. Then any function 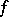 that is holomorphic in a neighbourhood of the set
that is holomorphic in a neighbourhood of the set 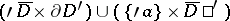 ,
, 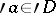 , can be holomorphically extended to
, can be holomorphically extended to 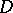 .
.
Hartogs' theorem is also taken to be the theorem on the removability of compact singularities (if 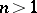 ); it is also known as the Osgood–Brown theorem .
); it is also known as the Osgood–Brown theorem .
The name Hartogs' theorem is also given to theorems on the continuous distribution of singular points if 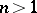 , on the analyticity of the set of singular points, and the theorem of uniform boundedness of a sequence of pointwise-bounded subharmonic functions.
, on the analyticity of the set of singular points, and the theorem of uniform boundedness of a sequence of pointwise-bounded subharmonic functions.
The theorems 1), 1a), 2), and 4) were first proved by F. Hartogs.
References
| [1] | F. Hartogs, "Zur Theorie der analytischen Funktionen mehrerer unabhängiger Veränderlichen, insbesondere über die Darstellung derselber durch Reihen welche nach Potentzen einer Veränderlichen fortschreiten" Math. Ann. , 62 (1906) pp. 1–88 |
| [2] | S. Bochner, W.T. Martin, "Several complex variables" , Princeton Univ. Press (1948) |
| [3] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
Comments
A version of Hartogs' theorem 3) (or the Osgood–Brown theorem) is as follows (cf. [a1], Thm. 2.3.2): Let 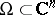 ,
, 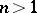 , be an open set and let
, be an open set and let 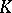 be a compact subset of
be a compact subset of  such that
such that 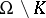 is connected. Then every holomorphic function on
is connected. Then every holomorphic function on 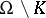 can be holomorphically extended to
can be holomorphically extended to  .
.
The result on sequences of pointwise-bounded subharmonic functions mentioned in 4) is also called Hartogs' lemma.
References
| [a1] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) pp. Chapt. 2.4 |
| [a2] | S.G. Krantz, "Function theory of several complex variables" , Wiley (1982) |
Hartogs theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hartogs_theorem&oldid=15022