Harmonic series
The series of numbers
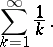 |
Each term of the harmonic series (beginning with the second) is the harmonic mean of its two contiguous terms (hence the name harmonic series). The harmonic series is divergent (G. Leibniz, 1673), and its partial sums
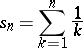 |
increase as 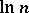 (L. Euler, 1740). There exists a constant
(L. Euler, 1740). There exists a constant  , known as the Euler constant, such that
, known as the Euler constant, such that  , where
, where  . The series
. The series
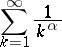 |
is called the generalized harmonic series; it is convergent for  and divergent for
and divergent for  .
.
Comments
For a proof of the expression for 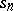 see, e.g., [a1], Thm. 422. Note that the series
see, e.g., [a1], Thm. 422. Note that the series 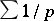 extended over all prime numbers
extended over all prime numbers 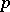 diverges also; see, e.g., [a1], Thm. 427, for an expression of its partial sums.
diverges also; see, e.g., [a1], Thm. 427, for an expression of its partial sums.
Generalized harmonic series are often used to test whether a given series is convergent or divergent by estimating in terms of 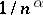 the order of the terms of the given series; see Series.
the order of the terms of the given series; see Series.
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) |
Harmonic series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Harmonic_series&oldid=17912