Hall polynomial
Hall polynomials are Lie polynomials obtained from elements of a given Hall set (cf. Lie polynomial; Hall set). They furnish a basis of the free Lie algebra (cf. Lie algebra, free) over a (finite or infinite) set of generators 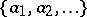 . Elements of a Hall set
. Elements of a Hall set  may be seen as completely bracketed words (or rooted planar binary trees with leaves labelled by generators
may be seen as completely bracketed words (or rooted planar binary trees with leaves labelled by generators 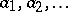 ; cf. also Binary tree). These are defined recursively as brackets
; cf. also Binary tree). These are defined recursively as brackets 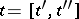 , where
, where  are bracketed words of lower weight; bracketed words of weight one correspond to the generators
are bracketed words of lower weight; bracketed words of weight one correspond to the generators 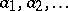 . The Hall polynomial associated with the Hall element
. The Hall polynomial associated with the Hall element  is then computed in the free associative ring (i.e. the ring of polynomials with non-commuting indeterminates
is then computed in the free associative ring (i.e. the ring of polynomials with non-commuting indeterminates 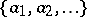 ) following the rule:
) following the rule:
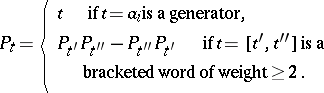 |
This basis of the free Lie algebra (cf. Lie algebra, free) is called the Hall basis (corresponding to the given Hall set). Sometimes this terminology is reserved for the basis arising from the basic commutator Hall set (or its left or right versions); cf. Hall set; Basic commutator.
A Hall set 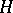 is totally ordered, thus inducing a total order on the set of polynomials
is totally ordered, thus inducing a total order on the set of polynomials 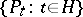 . One can show that any non-commutative polynomial is a sum of non-increasing products
. One can show that any non-commutative polynomial is a sum of non-increasing products 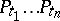 of Hall polynomials. This result is the well-known Poincaré–Birkhoff–Witt theorem for free Lie algebras (cf. also Lie algebra, free). One can prove this result combinatorially by first showing that any non-commutative polynomial is a sum of non-increasing products
of Hall polynomials. This result is the well-known Poincaré–Birkhoff–Witt theorem for free Lie algebras (cf. also Lie algebra, free). One can prove this result combinatorially by first showing that any non-commutative polynomial is a sum of non-increasing products 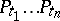 (with non-negative integer coefficients). This is accomplished using rewriting techniques (cf. [a1]); this idea is originally present in [a2]. A theorem stating that any word is a unique non-increasing product of Hall words then implies that these non-increasing products of Hall polynomials form a basis of the free associative algebra. It then follows that the set of Hall polynomials is linearly independent. In order to show that the set of Hall polynomials generate the free Lie algebra, one shows that the bracket
(with non-negative integer coefficients). This is accomplished using rewriting techniques (cf. [a1]); this idea is originally present in [a2]. A theorem stating that any word is a unique non-increasing product of Hall words then implies that these non-increasing products of Hall polynomials form a basis of the free associative algebra. It then follows that the set of Hall polynomials is linearly independent. In order to show that the set of Hall polynomials generate the free Lie algebra, one shows that the bracket 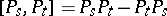 of any two Hall polynomials
of any two Hall polynomials 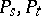 is a sum of Hall polynomials
is a sum of Hall polynomials 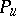 with
with 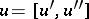 and
and 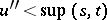 . This result is known as the Schützenberger lemma. Consequently, the set
. This result is known as the Schützenberger lemma. Consequently, the set 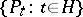 is a linear basis for the free Lie algebra over
is a linear basis for the free Lie algebra over 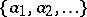 .
.
See also: Hall set; Hall word; Lie algebra, free; Lie polynomial.
There is a second notion of Hall polynomial, introduced by Philip Hall for studying the structure of finite modules over a commutative discrete valuation ring (cf. [a3]), whereas the Hall polynomials as defined above are usually attributed to Marshall Hall.
References
| [a1] | C. Reutenauer, "Free Lie algebras" , London Math. Soc. Monographs New Ser. , 7 , Oxford Univ. Press (1993) |
| [a2] | M. Hall, "A basis for free Lie rings and higher commutators in free groups" Proc. Amer. Math. Soc. , 1 (1950) pp. 57–581 |
| [a3] | I.G. MacDonald, "Symmetric functions and Hall polynomials" , Clarendon Press (1995) (Edition: Second) |
Hall polynomial. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hall_polynomial&oldid=13673