Haar measure
A non-zero positive measure 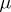 on the
on the 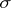 -ring
-ring 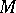 of subsets
of subsets 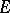 of a locally compact group
of a locally compact group 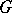 generated by the family of all compact subsets, taking finite values on all compact subsets of
generated by the family of all compact subsets, taking finite values on all compact subsets of 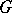 , and satisfying either the condition of left-invariance:
, and satisfying either the condition of left-invariance:
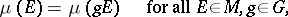 |
where 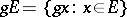 , or the condition of right-invariance:
, or the condition of right-invariance:
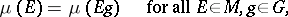 |
where 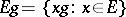 . Accordingly, one speaks of a left- or right-invariant Haar measure. Every Haar measure is
. Accordingly, one speaks of a left- or right-invariant Haar measure. Every Haar measure is 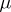 -regular, that is,
-regular, that is,
 |
for all 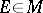 .
.
A left-invariant (and also a right-invariant) Haar measure exists and is unique, up to a positive factor; this was established by A. Haar [1] (under the additional assumption that the group 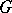 is separable).
is separable).
If 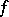 is a continuous function of compact support on
is a continuous function of compact support on 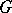 , then
, then 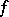 is integrable relative to a left-invariant Haar measure on
is integrable relative to a left-invariant Haar measure on 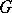 , and the corresponding integral is left-invariant (see Invariant integration), that is,
, and the corresponding integral is left-invariant (see Invariant integration), that is,
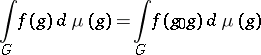 |
for all 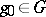 . A right-invariant Haar measure has the analogous property. The Haar measure of the whole group
. A right-invariant Haar measure has the analogous property. The Haar measure of the whole group 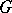 is finite if and only if
is finite if and only if 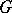 is compact.
is compact.
If 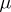 is a left-invariant Haar measure on
is a left-invariant Haar measure on 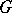 , then for every
, then for every 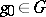 the following equality holds:
the following equality holds:
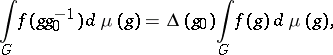 |
where  is a continuous homomorphism of
is a continuous homomorphism of 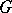 into the multiplicative group
into the multiplicative group 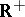 of positive real numbers that does not depend on the choice of the continuous function
of positive real numbers that does not depend on the choice of the continuous function 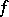 of compact support on
of compact support on 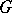 . The homomorphism
. The homomorphism  is called the modulus of
is called the modulus of 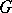 ; the measure
; the measure  is a right-invariant Haar measure on
is a right-invariant Haar measure on 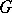 . If
. If 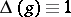 , then
, then 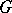 is called unimodular; in this case a left-invariant Haar measure is also right-invariant and is called (two-sided) invariant. In particular, every compact or discrete or Abelian locally compact group, and also every connected semi-simple or nilpotent Lie group, is unimodular. Unimodularity of a group
is called unimodular; in this case a left-invariant Haar measure is also right-invariant and is called (two-sided) invariant. In particular, every compact or discrete or Abelian locally compact group, and also every connected semi-simple or nilpotent Lie group, is unimodular. Unimodularity of a group 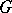 is also equivalent to the fact that every left-invariant Haar measure
is also equivalent to the fact that every left-invariant Haar measure 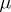 on
on 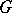 is also inversely invariant, that is,
is also inversely invariant, that is, 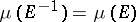 for all
for all 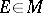 .
.
If 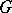 is a Lie group, then the integral with respect to a left-invariant (right-invariant) Haar measure on
is a Lie group, then the integral with respect to a left-invariant (right-invariant) Haar measure on 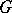 is defined by the formula
is defined by the formula
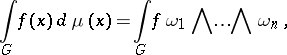 |
where the 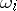 are linearly independent left-invariant (right-invariant) differential forms of order one on
are linearly independent left-invariant (right-invariant) differential forms of order one on 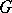 (see Maurer–Cartan form) and
(see Maurer–Cartan form) and 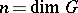 . The modulus of a Lie group
. The modulus of a Lie group 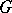 is defined by the formula
is defined by the formula
 |
where  is the adjoint representation (cf. Adjoint representation of a Lie group).
is the adjoint representation (cf. Adjoint representation of a Lie group).
Examples. 1) The Haar measure on the additive group  and on the quotient group
and on the quotient group 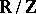 (the group of rotations of the circle) is the same as the ordinary Lebesgue measure. 2) The general linear group
(the group of rotations of the circle) is the same as the ordinary Lebesgue measure. 2) The general linear group 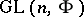 ,
, 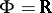 or
or 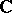 , is unimodular, and the Haar measure has the form
, is unimodular, and the Haar measure has the form
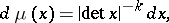 |
where 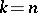 for
for  and
and 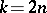 for
for 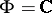 , and
, and 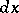 is the Lebesgue measure in the Euclidean space of all matrices of order
is the Lebesgue measure in the Euclidean space of all matrices of order  over the field
over the field 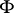 .
.
If 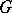 is a locally compact group,
is a locally compact group,  is a closed subgroup of it,
is a closed subgroup of it, 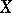 is the homogeneous space
is the homogeneous space 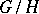 ,
, 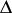 and
and 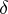 are the moduli of
are the moduli of 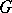 and
and 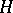 , respectively, and
, respectively, and  is a continuous homomorphism of
is a continuous homomorphism of 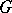 into
into 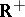 whose restriction to
whose restriction to 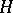 is given by the formula
is given by the formula
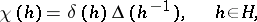 |
then there exists a positive measure  on the
on the 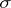 -ring
-ring 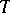 of sets
of sets  that is generated by the family of compact subsets of
that is generated by the family of compact subsets of 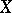 ; it is uniquely determined by the condition:
; it is uniquely determined by the condition:
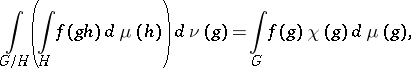 |
where 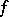 is any continuous function of compact support on
is any continuous function of compact support on 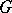 ,
, 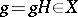 , and
, and
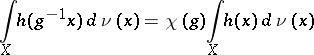 |
for all continuous functions  of compact support on
of compact support on  .
.
References
| [1] | A. Haar, "Der Massbegriff in der Theorie der kontinuierlichen Gruppen" Ann. of Math. (2) , 34 (1933) pp. 147–169 |
| [2] | N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French) |
| [3] | A. Weil, "l'Intégration dans les groupes topologiques et ses applications" , Hermann (1940) |
| [4] | L.H. Loomis, "An introduction to abstract harmonic analysis" , v. Nostrand (1953) |
| [5] | S. Helgason, "Differential geometry and symmetric spaces" , Acad. Press (1962) |
Comments
References
| [a1] | E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , 1–2 , Springer (1979) |
Haar measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Haar_measure&oldid=19105