Difference between revisions of "Hölder summation methods"
Ulf Rehmann (talk | contribs) m (moved Hölder summation methods to Holder summation methods: ascii title) |
Ulf Rehmann (talk | contribs) m (moved Holder summation methods to Hölder summation methods over redirect: accented title) |
(No difference)
| |
Revision as of 07:54, 26 March 2012
A collection of methods for summing series of numbers, introduced by O. Hölder [1] as a generalization of the summation method of arithmetical averages (cf. Arithmetical averages, summation method of). The series
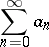 |
is summable by the Hölder method  to sum
to sum  if
if
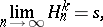 |
where
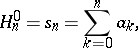 |
 |
 . In particular,
. In particular,  -summability of a series indicates that it converges in the ordinary sense;
-summability of a series indicates that it converges in the ordinary sense;  is the method of arithmetical averages. The
is the method of arithmetical averages. The  -methods are totally regular summation methods for any
-methods are totally regular summation methods for any  and are compatible for all
and are compatible for all 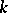 (cf. Compatibility of summation methods). The power of the method increases with increasing
(cf. Compatibility of summation methods). The power of the method increases with increasing 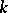 : If a series is summable to a sum
: If a series is summable to a sum  by the method
by the method  , it will also be summable to that sum by the method
, it will also be summable to that sum by the method 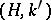 for any
for any 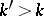 . For any
. For any  the method
the method  is equipotent and compatible with the Cesàro summation method of the same order
is equipotent and compatible with the Cesàro summation method of the same order  (cf. Cesàro summation methods). If a series is summable by the method
(cf. Cesàro summation methods). If a series is summable by the method 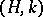 , its terms
, its terms 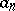 necessarily satisfy the condition
necessarily satisfy the condition  .
.
References
| [1] | O. Hölder, "Grenzwerthe von Reihen an der Konvergenzgrenze" Math. Ann. , 20 (1882) pp. 535–549 |
| [2] | G.H. Hardy, "Divergent series" , Oxford Univ. Press (1949) |
Hölder summation methods. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=H%C3%B6lder_summation_methods&oldid=22589