Difference between revisions of "Grothendieck space"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | A | + | <!-- |
| + | g1102501.png | ||
| + | $#A+1 = 53 n = 6 | ||
| + | $#C+1 = 53 : ~/encyclopedia/old_files/data/G110/G.1100250 Grothendieck space | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | A [[Banach space|Banach space]] $ X $ | ||
| + | with the property that for all separable Banach spaces $ Y $( | ||
| + | cf. [[Separable space|Separable space]]), every bounded [[Linear operator|linear operator]] $ T $ | ||
| + | from $ X $ | ||
| + | to $ Y $ | ||
| + | is weakly compact (i.e., $ T $ | ||
| + | sends bounded subsets of $ X $ | ||
| + | into weakly compact subsets of $ Y $). | ||
The above property is equivalent to each of the following assertions (see [[#References|[a4]]], [[#References|[a5]]], [[#References|[a9]]]). | The above property is equivalent to each of the following assertions (see [[#References|[a4]]], [[#References|[a5]]], [[#References|[a9]]]). | ||
| − | 1) Every weak- | + | 1) Every weak- $ * $ |
| + | convergent sequence in the dual space $ X ^ {*} $ | ||
| + | of $ X $ | ||
| + | is weakly convergent. | ||
| − | 2) Every bounded linear operator | + | 2) Every bounded linear operator $ T $ |
| + | from $ X $ | ||
| + | to $ c _ {0} $ | ||
| + | is weakly compact. | ||
| − | 3) For all Banach spaces | + | 3) For all Banach spaces $ Y $ |
| + | such that $ Y ^ {*} $ | ||
| + | has a weak- $ * $ | ||
| + | sequentially compact unit ball, every bounded linear operator from $ X $ | ||
| + | to $ Y $ | ||
| + | is weakly compact. | ||
| − | 4) For all weakly compactly generated Banach spaces | + | 4) For all weakly compactly generated Banach spaces $ Y $( |
| + | i.e., $ Y $ | ||
| + | is the closed linear span of a relatively weakly compact set), every bounded linear operator from $ X $ | ||
| + | to $ Y $ | ||
| + | is weakly compact. | ||
| − | 5) For an arbitrary Banach space | + | 5) For an arbitrary Banach space $ Y $, |
| + | the limit of any weakly convergent sequence of weakly compact operators from $ X $ | ||
| + | to $ Y $ | ||
| + | is also a weakly compact operator. | ||
| − | 6) For any Banach space | + | 6) For any Banach space $ Y $, |
| + | the limit of any strongly convergent sequence of weakly compact operators from $ X $ | ||
| + | to $ Y $ | ||
| + | is also a weakly compact operator. | ||
Hence, besides the definition given at the beginning, either 1) or 2) can also be used as the definition of a Grothendieck space. Quotient spaces and complemented subspaces of a Grothendieck space are also Grothendieck spaces. | Hence, besides the definition given at the beginning, either 1) or 2) can also be used as the definition of a Grothendieck space. Quotient spaces and complemented subspaces of a Grothendieck space are also Grothendieck spaces. | ||
| − | Reflexive Banach spaces are obvious examples of Grothendieck spaces (cf. [[Reflexive space|Reflexive space]]). Every separable quotient space of a Grothendieck space is necessarily reflexive. The first non-trivial example of a Grothendieck space is the space | + | Reflexive Banach spaces are obvious examples of Grothendieck spaces (cf. [[Reflexive space|Reflexive space]]). Every separable quotient space of a Grothendieck space is necessarily reflexive. The first non-trivial example of a Grothendieck space is the space $ C ( \Omega ) $ |
| + | of continuous functions on a compact Stonean space $ \Omega $( | ||
| + | i.e., a compact [[Hausdorff space|Hausdorff space]] in which each open set has an open closure) [[#References|[a6]]]. | ||
| − | Other examples of Grothendieck spaces are: | + | Other examples of Grothendieck spaces are: $ C ( \Omega ) $, |
| + | where $ \Omega $ | ||
| + | is a compact $ \sigma $- | ||
| + | Stonean space (each open $ F _ \sigma $- | ||
| + | set has an open closure) or a compact $ F $- | ||
| + | space (any two disjoint open $ F _ \sigma $- | ||
| + | sets have disjoint closures) (see [[#References|[a1]]], [[#References|[a10]]]); $ L ^ \infty ( \mu ) $, | ||
| + | where $ \mu $ | ||
| + | is a positive measure; $ B ( S, \Sigma ) $, | ||
| + | where $ \Sigma $ | ||
| + | is a $ \sigma $- | ||
| + | algebra of subsets of $ S $; | ||
| + | injective Banach spaces; the Hardy space $ H ^ \infty ( D ) $ | ||
| + | of all bounded analytic functions on the open unit disc $ D $[[#References|[a2]]]; and von Neumann algebras [[#References|[a8]]]. | ||
| − | A uniformly bounded | + | A uniformly bounded $ C _ {0} $- |
| + | semi-group of operators (cf. [[Semi-group of operators|Semi-group of operators]]) on a Grothendieck space is strongly ergodic if and only if the weak- $ * $ | ||
| + | closure and the strong closure of the range of the dual operator of the generator $ A $ | ||
| + | coincide [[#References|[a11]]]. If $ C ( K ) $ | ||
| + | is a Grothendieck space, then every sequence $ \{ T _ {n} \} $ | ||
| + | of contractions on $ C ( K ) $ | ||
| + | which converges to the identity in the strong operator topology actually converges in the uniform operator topology (see [[#References|[a3]]], [[#References|[a7]]]). In particular, this implies equivalence of strong continuity and uniform continuity for contraction $ C _ {0} $- | ||
| + | semi-groups on $ C ( K ) $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T. Ando, "Convergent sequences of finitely additive measures" ''Pacific J. Math.'' , '''11''' (1961) pp. 395–404</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Bourgain, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110250/g11025057.png" /> is a Grothendieck space" ''Studia Math.'' , '''75''' (1983) pp. 193–216</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> Th. Coulhon, "Suites d'operateurs sur un espace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110250/g11025058.png" /> de Grothendieck" ''C.R. Acad. Sci. Paris'' , '''298''' (1984) pp. 13–15</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J. Diestel, "Grothendieck spaces and vector measures" , ''Vector and Operator Valued Measures and Applications'' , Acad. Press (1973) pp. 97–108</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J. Diestel, J.J. Uhl, Jr., "Vector measures" , ''Math. Surveys'' , '''15''' , Amer. Math. Soc. (1977)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> A. Grothendieck, "Sur les applications linéaires faiblement compactes d'espaces du type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110250/g11025059.png" />" ''Canadian J. Math.'' , '''5''' (1953) pp. 129–173</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> H.P. Lotz, "Uniform convergence of operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110250/g11025060.png" /> and similar spaces" ''Math. Z.'' , '''190''' (1985) pp. 207–220</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> H. Pfitzner, "Weak compactness in the dual of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110250/g11025061.png" />-algebra is determined commutatively" ''Math. Ann.'' , '''298''' (1994) pp. 349–371</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> F. Rábiger, "Beiträge zur Strukturtheorie der Grothendieck-Räume" ''Sitzungsber. Heidelberger Akad. Wissenschaft. Math.-Naturwiss. Kl. Abh.'' , '''4''' (1985)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> G. L. Seever, "Measures on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110250/g11025062.png" />-spaces" ''Trans. Amer. Math. Soc.'' , '''133''' (1968) pp. 267–280</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> S.-Y. Shaw, "Ergodic theorems for semigroups of operators on a Grothendieck space" ''Proc. Japan Acad.'' , '''59 (A)''' (1983) pp. 132–135</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T. Ando, "Convergent sequences of finitely additive measures" ''Pacific J. Math.'' , '''11''' (1961) pp. 395–404</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Bourgain, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110250/g11025057.png" /> is a Grothendieck space" ''Studia Math.'' , '''75''' (1983) pp. 193–216</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> Th. Coulhon, "Suites d'operateurs sur un espace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110250/g11025058.png" /> de Grothendieck" ''C.R. Acad. Sci. Paris'' , '''298''' (1984) pp. 13–15</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J. Diestel, "Grothendieck spaces and vector measures" , ''Vector and Operator Valued Measures and Applications'' , Acad. Press (1973) pp. 97–108</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J. Diestel, J.J. Uhl, Jr., "Vector measures" , ''Math. Surveys'' , '''15''' , Amer. Math. Soc. (1977)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> A. Grothendieck, "Sur les applications linéaires faiblement compactes d'espaces du type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110250/g11025059.png" />" ''Canadian J. Math.'' , '''5''' (1953) pp. 129–173</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> H.P. Lotz, "Uniform convergence of operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110250/g11025060.png" /> and similar spaces" ''Math. Z.'' , '''190''' (1985) pp. 207–220</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> H. Pfitzner, "Weak compactness in the dual of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110250/g11025061.png" />-algebra is determined commutatively" ''Math. Ann.'' , '''298''' (1994) pp. 349–371</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> F. Rábiger, "Beiträge zur Strukturtheorie der Grothendieck-Räume" ''Sitzungsber. Heidelberger Akad. Wissenschaft. Math.-Naturwiss. Kl. Abh.'' , '''4''' (1985)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> G. L. Seever, "Measures on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110250/g11025062.png" />-spaces" ''Trans. Amer. Math. Soc.'' , '''133''' (1968) pp. 267–280</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> S.-Y. Shaw, "Ergodic theorems for semigroups of operators on a Grothendieck space" ''Proc. Japan Acad.'' , '''59 (A)''' (1983) pp. 132–135</TD></TR></table> | ||
Revision as of 19:42, 5 June 2020
A Banach space $ X $
with the property that for all separable Banach spaces $ Y $(
cf. Separable space), every bounded linear operator $ T $
from $ X $
to $ Y $
is weakly compact (i.e., $ T $
sends bounded subsets of $ X $
into weakly compact subsets of $ Y $).
The above property is equivalent to each of the following assertions (see [a4], [a5], [a9]).
1) Every weak- $ * $ convergent sequence in the dual space $ X ^ {*} $ of $ X $ is weakly convergent.
2) Every bounded linear operator $ T $ from $ X $ to $ c _ {0} $ is weakly compact.
3) For all Banach spaces $ Y $ such that $ Y ^ {*} $ has a weak- $ * $ sequentially compact unit ball, every bounded linear operator from $ X $ to $ Y $ is weakly compact.
4) For all weakly compactly generated Banach spaces $ Y $( i.e., $ Y $ is the closed linear span of a relatively weakly compact set), every bounded linear operator from $ X $ to $ Y $ is weakly compact.
5) For an arbitrary Banach space $ Y $, the limit of any weakly convergent sequence of weakly compact operators from $ X $ to $ Y $ is also a weakly compact operator.
6) For any Banach space $ Y $, the limit of any strongly convergent sequence of weakly compact operators from $ X $ to $ Y $ is also a weakly compact operator.
Hence, besides the definition given at the beginning, either 1) or 2) can also be used as the definition of a Grothendieck space. Quotient spaces and complemented subspaces of a Grothendieck space are also Grothendieck spaces.
Reflexive Banach spaces are obvious examples of Grothendieck spaces (cf. Reflexive space). Every separable quotient space of a Grothendieck space is necessarily reflexive. The first non-trivial example of a Grothendieck space is the space $ C ( \Omega ) $ of continuous functions on a compact Stonean space $ \Omega $( i.e., a compact Hausdorff space in which each open set has an open closure) [a6].
Other examples of Grothendieck spaces are: $ C ( \Omega ) $, where $ \Omega $ is a compact $ \sigma $- Stonean space (each open $ F _ \sigma $- set has an open closure) or a compact $ F $- space (any two disjoint open $ F _ \sigma $- sets have disjoint closures) (see [a1], [a10]); $ L ^ \infty ( \mu ) $, where $ \mu $ is a positive measure; $ B ( S, \Sigma ) $, where $ \Sigma $ is a $ \sigma $- algebra of subsets of $ S $; injective Banach spaces; the Hardy space $ H ^ \infty ( D ) $ of all bounded analytic functions on the open unit disc $ D $[a2]; and von Neumann algebras [a8].
A uniformly bounded $ C _ {0} $- semi-group of operators (cf. Semi-group of operators) on a Grothendieck space is strongly ergodic if and only if the weak- $ * $ closure and the strong closure of the range of the dual operator of the generator $ A $ coincide [a11]. If $ C ( K ) $ is a Grothendieck space, then every sequence $ \{ T _ {n} \} $ of contractions on $ C ( K ) $ which converges to the identity in the strong operator topology actually converges in the uniform operator topology (see [a3], [a7]). In particular, this implies equivalence of strong continuity and uniform continuity for contraction $ C _ {0} $- semi-groups on $ C ( K ) $.
References
| [a1] | T. Ando, "Convergent sequences of finitely additive measures" Pacific J. Math. , 11 (1961) pp. 395–404 |
| [a2] | J. Bourgain, "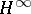 is a Grothendieck space" Studia Math. , 75 (1983) pp. 193–216 is a Grothendieck space" Studia Math. , 75 (1983) pp. 193–216 |
| [a3] | Th. Coulhon, "Suites d'operateurs sur un espace  de Grothendieck" C.R. Acad. Sci. Paris , 298 (1984) pp. 13–15 de Grothendieck" C.R. Acad. Sci. Paris , 298 (1984) pp. 13–15 |
| [a4] | J. Diestel, "Grothendieck spaces and vector measures" , Vector and Operator Valued Measures and Applications , Acad. Press (1973) pp. 97–108 |
| [a5] | J. Diestel, J.J. Uhl, Jr., "Vector measures" , Math. Surveys , 15 , Amer. Math. Soc. (1977) |
| [a6] | A. Grothendieck, "Sur les applications linéaires faiblement compactes d'espaces du type  " Canadian J. Math. , 5 (1953) pp. 129–173 " Canadian J. Math. , 5 (1953) pp. 129–173 |
| [a7] | H.P. Lotz, "Uniform convergence of operators on  and similar spaces" Math. Z. , 190 (1985) pp. 207–220 and similar spaces" Math. Z. , 190 (1985) pp. 207–220 |
| [a8] | H. Pfitzner, "Weak compactness in the dual of a  -algebra is determined commutatively" Math. Ann. , 298 (1994) pp. 349–371 -algebra is determined commutatively" Math. Ann. , 298 (1994) pp. 349–371 |
| [a9] | F. Rábiger, "Beiträge zur Strukturtheorie der Grothendieck-Räume" Sitzungsber. Heidelberger Akad. Wissenschaft. Math.-Naturwiss. Kl. Abh. , 4 (1985) |
| [a10] | G. L. Seever, "Measures on  -spaces" Trans. Amer. Math. Soc. , 133 (1968) pp. 267–280 -spaces" Trans. Amer. Math. Soc. , 133 (1968) pp. 267–280 |
| [a11] | S.-Y. Shaw, "Ergodic theorems for semigroups of operators on a Grothendieck space" Proc. Japan Acad. , 59 (A) (1983) pp. 132–135 |
Grothendieck space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Grothendieck_space&oldid=15530