Green space
A topological space  on which harmonic and superharmonic functions (cf. Harmonic function; Subharmonic function) are defined and for which a Green function exists (for the Dirichlet problem in the class of harmonic functions) or, which amounts to the same thing, for which there exists a non-constant superharmonic function. More exactly, let
on which harmonic and superharmonic functions (cf. Harmonic function; Subharmonic function) are defined and for which a Green function exists (for the Dirichlet problem in the class of harmonic functions) or, which amounts to the same thing, for which there exists a non-constant superharmonic function. More exactly, let  be an
be an  -space, i.e. a connected separable topological space in which: 1) each point
-space, i.e. a connected separable topological space in which: 1) each point  has an open neighbourhood
has an open neighbourhood  homeomorphic to some open set
homeomorphic to some open set  of a Euclidean space
of a Euclidean space  (or of its Aleksandrov compactification
(or of its Aleksandrov compactification  ); and 2) the images of any non-empty intersection
); and 2) the images of any non-empty intersection  (under the two homeomorphisms to
(under the two homeomorphisms to 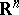 or
or 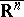 ) of two neighbourhoods in
) of two neighbourhoods in  and
and 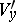 are isometric, and are conformally equivalent if
are isometric, and are conformally equivalent if  . Harmonic and superharmonic functions on an
. Harmonic and superharmonic functions on an 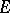 -space
-space  are locally defined by passing to the images
are locally defined by passing to the images  . If, in addition, there exists a non-constant positive superharmonic function on
. If, in addition, there exists a non-constant positive superharmonic function on  or, which amounts to the same thing, a positive potential,
or, which amounts to the same thing, a positive potential,  is known as a Green space. Thus, the Euclidean space
is known as a Green space. Thus, the Euclidean space  , its compactification
, its compactification  (
(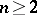 ) and Riemann surfaces are all
) and Riemann surfaces are all  -spaces. Here,
-spaces. Here, 
 and Riemann surfaces of hyperbolic type (cf. Riemann surfaces, classification of) are Green spaces, while
and Riemann surfaces of hyperbolic type (cf. Riemann surfaces, classification of) are Green spaces, while  and Riemann surfaces of parabolic type are not. Any domain in a Green space
and Riemann surfaces of parabolic type are not. Any domain in a Green space  is again a Green space.
is again a Green space.
A harmonic space 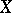 with a positive potential on it can also be regarded as a generalization of a Green space in the framework of axiomatic potential theory (cf. Potential theory, abstract).
with a positive potential on it can also be regarded as a generalization of a Green space in the framework of axiomatic potential theory (cf. Potential theory, abstract).
References
| [1] | M. Brelot, "On topologies and boundaries in potential theory" , Springer (1971) |
| [2] | M. Brélot, G. Choquet, "Espaces et lignes de Green" Ann. Inst. Fourier , 3 (1952) pp. 199–263 |
Green space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Green_space&oldid=12148