Graded algebra
An algebra  whose additive group can be represented in the form of a (weak) direct sum of groups
whose additive group can be represented in the form of a (weak) direct sum of groups  ,
,  where
where  for any
for any  . As a result, the additive group of a graded algebra (considered as a module over the ring of integers) is a positively graded module. As an example of a graded algebra one can quote the algebra
. As a result, the additive group of a graded algebra (considered as a module over the ring of integers) is a positively graded module. As an example of a graded algebra one can quote the algebra  of polynomials over a field
of polynomials over a field  , where
, where  is the subspace generated by the monomials of degree
is the subspace generated by the monomials of degree  (
( ). One can also define a graded algebra
). One can also define a graded algebra  in a more general manner as an algebra whose additive group can be represented as a direct sum of groups
in a more general manner as an algebra whose additive group can be represented as a direct sum of groups 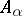 , where
, where  runs through a certain commutative semi-group
runs through a certain commutative semi-group  and
and  for any
for any  . The concept of a filtered algebra is closely connected with that of a graded algebra. It is in fact possible to define, in a natural manner, an ascending filtration
. The concept of a filtered algebra is closely connected with that of a graded algebra. It is in fact possible to define, in a natural manner, an ascending filtration
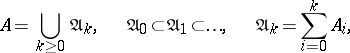 |
on each graded algebra 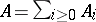 . Conversely, if
. Conversely, if  is a filtered algebra
is a filtered algebra  , then one defines the graded algebra
, then one defines the graded algebra  (where
(where  ,
, 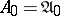 ), which is called the graded algebra associated with
), which is called the graded algebra associated with  . A graded ring is defined in a similar manner.
. A graded ring is defined in a similar manner.
Comments
For an arbitrary group  one may define a gradation of type
one may define a gradation of type 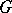 on an algebra
on an algebra 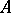 , i.e.
, i.e.  where each
where each  is an additive subgroup of
is an additive subgroup of  and
and  for all
for all  . The group algebra
. The group algebra  over the field
over the field 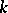 , as well as crossed products
, as well as crossed products  defined by a group morphism
defined by a group morphism  and a
and a  -cocycle
-cocycle  , are examples of
, are examples of 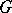 -graded algebras (see also Cross product). The use of
-graded algebras (see also Cross product). The use of  -gradations that are not necessarily positive gradations allows one to consider the graded rings associated to
-gradations that are not necessarily positive gradations allows one to consider the graded rings associated to  -adic filtrations on a ring
-adic filtrations on a ring 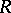 ; for an ideal
; for an ideal 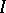 of
of 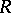 the
the  -adic filtration is given by a descending chain
-adic filtration is given by a descending chain 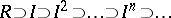 , and then
, and then  , where
, where 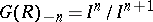 is negatively graded.
is negatively graded.
References
| [a1] | N. Bourbaki, "Algèbre commutative" , Eléments de mathématiques , Hermann (1961) pp. Chapt. 3. Graduations, filtrations, et topologies |
| [a2] | C. Nâstâsescu, F. van Oystaeyen, "Graded ring theory" , North-Holland (1982) |
Graded algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Graded_algebra&oldid=17736