Geometric progression
A sequence of numbers each one of which is equal to the preceding one multiplied by a number  (the denominator of the progression). A geometric progression is called increasing if
(the denominator of the progression). A geometric progression is called increasing if  , and decreasing if
, and decreasing if  ; if
; if  , one has a sign-alternating progression. Any term of a geometric progression
, one has a sign-alternating progression. Any term of a geometric progression  can be expressed by its first term
can be expressed by its first term  and the denominator
and the denominator  by the formula
by the formula
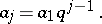 |
The sum of the first  terms of a geometric progression (with
terms of a geometric progression (with  ) is given by the formula
) is given by the formula
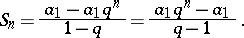 |
If 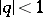 , the sum
, the sum 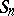 tends to the limit
tends to the limit  as
as  increases without limit. This number
increases without limit. This number  is known as the sum of the infinitely-decreasing geometric progression.
is known as the sum of the infinitely-decreasing geometric progression.
The expression
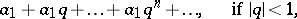 |
is the simplest example of a convergent series — a geometric series; the number  is the sum of the geometric series.
is the sum of the geometric series.
The term "geometric progression" is connected with the following property of any term of a geometric progression with positive terms: 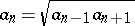 , i.e. any term is the geometric mean of the term which precedes it and the term which follows it.
, i.e. any term is the geometric mean of the term which precedes it and the term which follows it.
Geometric progression. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geometric_progression&oldid=12512