Genus of a surface
From Encyclopedia of Mathematics
A numerical birational invariant of a two-dimensional algebraic variety defined over an algebraically closed field 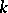 . There are two different genera — the arithmetic genus and the geometric genus. The geometric genus
. There are two different genera — the arithmetic genus and the geometric genus. The geometric genus 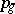 of a complete smooth algebraic surface
of a complete smooth algebraic surface 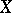 is equal to
is equal to
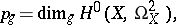 |
i.e. to the dimension of the space of regular differential  -forms (cf. Differential form) on
-forms (cf. Differential form) on 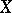 . The arithmetic genus
. The arithmetic genus 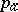 of a complete smooth algebraic surface
of a complete smooth algebraic surface  is equal to
is equal to
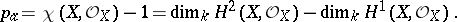 |
The geometric and arithmetic genera of a complete smooth algebraic surface 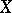 are related by the formula
are related by the formula 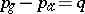 , where
, where 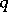 is the irregularity of
is the irregularity of 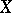 , which is equal to the dimension of the space of regular differential
, which is equal to the dimension of the space of regular differential 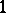 -forms on
-forms on 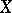 .
.
References
| [1] | I.R., et al. Shafarevich, "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) |
Comments
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
| [a2] | A. van de Ven, "Compact complex surfaces" , Springer (1984) |
| [a3] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) |
How to Cite This Entry:
Genus of a surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Genus_of_a_surface&oldid=16127
Genus of a surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Genus_of_a_surface&oldid=16127
This article was adapted from an original article by Vik.S. Kulikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article