Gaussian process
A real stochastic process  ,
,  , all finite-dimensional distributions of which are Gaussian, i.e. for any
, all finite-dimensional distributions of which are Gaussian, i.e. for any  the characteristic function of the joint probability distribution of the random variables
the characteristic function of the joint probability distribution of the random variables  has the form
has the form
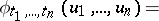 |
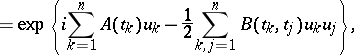 |
where  is the mathematical expectation and
is the mathematical expectation and
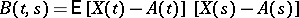 |
is the covariance function. The probability distribution  of a Gaussian process is completely determined by its mathematical expectation
of a Gaussian process is completely determined by its mathematical expectation 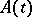 and by the covariance function
and by the covariance function 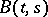 ,
, 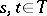 . For any function
. For any function 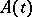 and any positive-definite function
and any positive-definite function 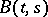 there exists a Gaussian process
there exists a Gaussian process  with expectation
with expectation 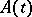 and covariance function
and covariance function 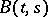 . A multi-dimensional stochastic process with vector values
. A multi-dimensional stochastic process with vector values
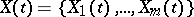 |
is called Gaussian if the joint probability distributions of arbitrary variables
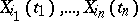 |
are Gaussian.
A complex Gaussian process 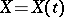 ,
,  , is a process of the form
, is a process of the form
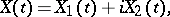 |
in which 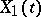 ,
, 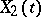 jointly form a two-dimensional real Gaussian process. Regarding a complex Gaussian process
jointly form a two-dimensional real Gaussian process. Regarding a complex Gaussian process 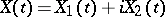 one additional stipulation is imposed:
one additional stipulation is imposed:
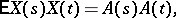 |
where
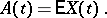 |
This condition is introduced in order to ensure the preservation of the equivalence between non-correlation and independence, which is a property of ordinary Gaussian random variables. It may be rewritten as follows:
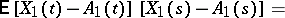 |
 |
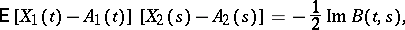 |
where
 |
is the covariance function of the process 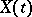 and
and
 |
A linear generalized stochastic process 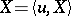 ,
, 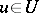 , on a linear space
, on a linear space 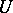 is called a generalized Gaussian process if its characteristic functional
is called a generalized Gaussian process if its characteristic functional  has the form
has the form
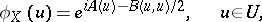 |
where  is the mathematical expectation of the generalized process
is the mathematical expectation of the generalized process 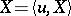 and
and
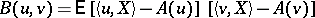 |
is its covariance functional.
Let 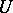 be a Hilbert space with scalar product
be a Hilbert space with scalar product 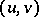 ,
, 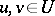 . A random variable
. A random variable 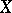 with values in
with values in 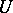 is called Gaussian if
is called Gaussian if 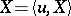 ,
, 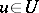 , is a generalized Gaussian process. The mathematical expectation
, is a generalized Gaussian process. The mathematical expectation 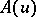 is a continuous linear functional, while the covariance function
is a continuous linear functional, while the covariance function 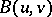 is a continuous bilinear functional on the Hilbert space
is a continuous bilinear functional on the Hilbert space 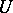 , and
, and
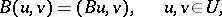 |
where the positive operator 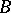 is a nuclear operator, called the covariance operator. For any such
is a nuclear operator, called the covariance operator. For any such 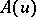 and
and 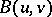 there exists a Gaussian variable
there exists a Gaussian variable 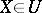 such that the generalized process
such that the generalized process 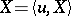 ,
, 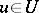 , has expectation
, has expectation 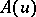 and covariance function
and covariance function  .
.
Example. Let 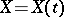 be a Gaussian process on the segment
be a Gaussian process on the segment 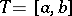 , let the process
, let the process 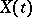 be measurable, and let also
be measurable, and let also
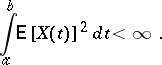 |
Then almost-all the trajectories of 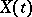 ,
, 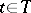 , will belong to the space of square-integrable functions
, will belong to the space of square-integrable functions 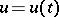 on
on 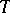 with the scalar product
with the scalar product
 |
The formula
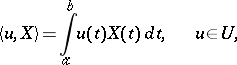 |
defines a generalized Gaussian process on this space 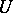 . The expectation and the covariance functional of the generalized process
. The expectation and the covariance functional of the generalized process 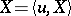 are expressed by the formulas
are expressed by the formulas
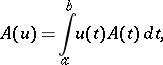 |
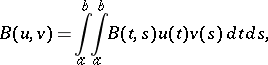 |
where 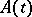 and
and 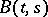 are, respectively, the expectation and the covariance function of the initial process
are, respectively, the expectation and the covariance function of the initial process 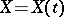 on
on 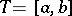 .
.
Almost-all the fundamental properties of a Gaussian process 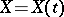 (the parameter
(the parameter 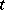 runs through an arbitrary set
runs through an arbitrary set 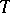 ) may be expressed in geometrical terms if the process is considered as a curve in the Hilbert space
) may be expressed in geometrical terms if the process is considered as a curve in the Hilbert space 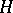 of all random variables
of all random variables 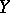 ,
, 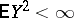 , with the scalar product
, with the scalar product  for which
for which
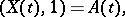 |
and
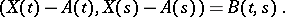 |
Yu.A. Rozanov
Gaussian processes that are stationary in the narrow sense may be realized by way of certain dynamical systems (a shift in the space of trajectories [1]). The dynamical systems obtained (which are sometimes denoted as normal, on account of the resemblance to the normal probability distributions) are of interest as examples of dynamical systems with a continuous spectrum the properties of which can be more exhaustively studied owing to the decomposition of 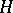 introduced in [4], [5]. The first actual examples of dynamical systems with "non-classical" spectral properties have been constructed in this way.
introduced in [4], [5]. The first actual examples of dynamical systems with "non-classical" spectral properties have been constructed in this way.
References
| [1] | J.L. Doob, "Stochastic processes" , Chapman & Hall (1953) |
| [2] | I.A. Ibragimov, Yu.A. Rozanov, "Gaussian random processes" , Springer (1978) (Translated from Russian) |
| [3] | H. Cramér, M.R. Leadbetter, "Stationary and related stochastic processes" , Wiley (1967) pp. Chapts. 33–34 |
| [4] | K. Itô, "Multiple Wiener integral" J. Math. Soc. Japan , 3 : 1 (1951) pp. 157–169 |
| [5] | K. Itô, "Complex multiple Wiener integral" Japan J. Math. , 22 (1952) pp. 63–86 |
D.V. Anosov
Comments
A Gaussian process is sometimes called a normal process. See Stationary stochastic process for details about stationary Gaussian processes.
During the last twenty years hard work has been done by the American and French school in studying the regularity of the paths of a (real-valued) Gaussian process  with respect to the (pseudo-)metric
with respect to the (pseudo-)metric 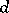 on
on 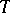 defined by
defined by
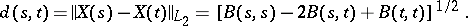 |
See [a2] for a history and an exposition of the definite results. This work produced also tools in order to study (non-Gaussian) Banach-valued stochastic processes.
References
| [a1] | J. Neveu, "Processus aléatoires Gaussiens" , Univ. Montréal (1968) |
| [a2] | X. Fernique, "Fonctions aléatores gaussiennes, les résultats de M. Talagrand" Astérisque , 145–146 (1987) pp. 177–186 (Exp. 660, Sém. Bourbaki 1985/86) |
Gaussian process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gaussian_process&oldid=14281