Difference between revisions of "Gamma-invariant in the theory of modular forms"
m (link) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | g1100602.png | ||
| + | $#A+1 = 26 n = 1 | ||
| + | $#C+1 = 26 : ~/encyclopedia/old_files/data/G110/G.1100060 Gamma\AAhinvariant in the theory of modular forms, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | '' $ \Gamma $- | |
| + | invariant'' | ||
| − | + | Let $ G ( \Gamma ) $ | |
| + | be a [[Fuchsian group|Fuchsian group]] of the first kind, acting on the real hyperbolic plane $ H $. | ||
| + | Suppose that $ G $ | ||
| + | is a group of genus zero, i.e. the number of hyperbolic generators of $ G $ | ||
| + | is equal to zero. Let $ J $ | ||
| + | be a [[Conformal mapping|conformal mapping]] of the [[Fundamental domain|fundamental domain]] $ F $ | ||
| + | of $ G $ | ||
| + | onto the complex plane $ \mathbf C $ | ||
| + | that is extended as an [[Automorphic function|automorphic function]] to the whole of $ H $. | ||
| + | In other words, there exists an isomorphism of complex manifolds between the compactification of $ F $ | ||
| + | and the Riemann sphere which induces an univalent automorphic function $ J $ | ||
| + | on $ H $. | ||
| + | The function $ J $ | ||
| + | is defined up to a [[Fractional-linear mapping|fractional-linear mapping]] and satisfies the Schwarz differential equation (see [[#References|[a1]]]; see also [[Schwarz differential|Schwarz differential]]; [[Schwarz equation|Schwarz equation]]). | ||
| − | Gamma-invariants play an important role in various domains of mathematics and mathematical physics. For example, in [[Algebraic number theory|algebraic number theory]] the modular equation and its generalizations were used by Ch. Hermite and L. Kronecker to obtain the transcendental solution of the general [[Algebraic equation|algebraic equation]] of the fifth degree (see [[#References|[a2]]]). The modular invariant is important in the extension of the [[Kronecker theorem|Kronecker theorem]] on Abelian fields for imaginary quadratic ground fields and, more generally, in [[Class field theory|class field theory]] (see [[#References|[a3]]], [[#References|[a4]]]). Other important interpretations and developments of this theory are in [[Algebraic geometry|algebraic geometry]] (the theory of elliptic and modular curves) and in the theory of Dirichlet | + | The function $ J $ |
| + | is called a gamma- or automorphic (modular) invariant. | ||
| + | |||
| + | The first example of a gamma-invariant, $ k ( 2 ) $, | ||
| + | was discovered and investigated in the Abel–Gauss–Jacobi and Eisenstein–Weierstrass theory of elliptic and elliptic modular functions between 1820– 1850 (see [[#References|[a2]]]). The function $ k ( 2 ) $ | ||
| + | was obtained as a function of the quotient of the periods of a certain [[Elliptic integral|elliptic integral]]. It corresponds to the level-two congruence subgroup of the [[Modular group|modular group]] $ { \mathop{\rm PSL} } ( 2, \mathbf Z ) $. | ||
| + | For the modular group itself, the invariant $ J $ | ||
| + | was constructed in 1877 by R. Dedekind and, one year later and independently, by F. Klein. In this definition, $ J $ | ||
| + | is a certain rational function of the two main modular holomorphic [[Eisenstein series]] $ E ( 4 ) $ | ||
| + | and $ E ( 6 ) $. | ||
| + | These two classical invariants $ k ( 2 ) $ | ||
| + | and $ J $ | ||
| + | satisfy the modular equation. | ||
| + | |||
| + | Gamma-invariants play an important role in various domains of mathematics and mathematical physics. For example, in [[Algebraic number theory|algebraic number theory]] the modular equation and its generalizations were used by Ch. Hermite and L. Kronecker to obtain the transcendental solution of the general [[Algebraic equation|algebraic equation]] of the fifth degree (see [[#References|[a2]]]). The modular invariant is important in the extension of the [[Kronecker theorem|Kronecker theorem]] on Abelian fields for imaginary quadratic ground fields and, more generally, in [[Class field theory|class field theory]] (see [[#References|[a3]]], [[#References|[a4]]]). Other important interpretations and developments of this theory are in [[Algebraic geometry|algebraic geometry]] (the theory of elliptic and modular curves) and in the theory of Dirichlet $ L $- | ||
| + | series (see [[#References|[a5]]], [[#References|[a6]]]; see also [[Dirichlet L-function|Dirichlet $ L $- | ||
| + | function]]). | ||
Automorphic invariants participate also in Selberg's theory of the trace formula for constructing resolvents of automorphic Laplacians (automorphic Green functions) (see [[#References|[a1]]], [[#References|[a6]]]). | Automorphic invariants participate also in Selberg's theory of the trace formula for constructing resolvents of automorphic Laplacians (automorphic Green functions) (see [[#References|[a1]]], [[#References|[a6]]]). | ||
Latest revision as of 19:41, 5 June 2020
$ \Gamma $-
invariant
Let $ G ( \Gamma ) $ be a Fuchsian group of the first kind, acting on the real hyperbolic plane $ H $. Suppose that $ G $ is a group of genus zero, i.e. the number of hyperbolic generators of $ G $ is equal to zero. Let $ J $ be a conformal mapping of the fundamental domain $ F $ of $ G $ onto the complex plane $ \mathbf C $ that is extended as an automorphic function to the whole of $ H $. In other words, there exists an isomorphism of complex manifolds between the compactification of $ F $ and the Riemann sphere which induces an univalent automorphic function $ J $ on $ H $. The function $ J $ is defined up to a fractional-linear mapping and satisfies the Schwarz differential equation (see [a1]; see also Schwarz differential; Schwarz equation).
The function $ J $ is called a gamma- or automorphic (modular) invariant.
The first example of a gamma-invariant, $ k ( 2 ) $, was discovered and investigated in the Abel–Gauss–Jacobi and Eisenstein–Weierstrass theory of elliptic and elliptic modular functions between 1820– 1850 (see [a2]). The function $ k ( 2 ) $ was obtained as a function of the quotient of the periods of a certain elliptic integral. It corresponds to the level-two congruence subgroup of the modular group $ { \mathop{\rm PSL} } ( 2, \mathbf Z ) $. For the modular group itself, the invariant $ J $ was constructed in 1877 by R. Dedekind and, one year later and independently, by F. Klein. In this definition, $ J $ is a certain rational function of the two main modular holomorphic Eisenstein series $ E ( 4 ) $ and $ E ( 6 ) $. These two classical invariants $ k ( 2 ) $ and $ J $ satisfy the modular equation.
Gamma-invariants play an important role in various domains of mathematics and mathematical physics. For example, in algebraic number theory the modular equation and its generalizations were used by Ch. Hermite and L. Kronecker to obtain the transcendental solution of the general algebraic equation of the fifth degree (see [a2]). The modular invariant is important in the extension of the Kronecker theorem on Abelian fields for imaginary quadratic ground fields and, more generally, in class field theory (see [a3], [a4]). Other important interpretations and developments of this theory are in algebraic geometry (the theory of elliptic and modular curves) and in the theory of Dirichlet $ L $- series (see [a5], [a6]; see also Dirichlet $ L $- function).
Automorphic invariants participate also in Selberg's theory of the trace formula for constructing resolvents of automorphic Laplacians (automorphic Green functions) (see [a1], [a6]).
In [a7] modular equations are used for investigating non-congruence subgroups of the modular group.
There is a mysterious relationship between simple finite groups (the Monster, cf. Simple finite group) and automorphic invariants (see [a8], [a9], [a10]). In particular, via this relation there is a connection between modular invariants and mathematical physics (string theory [a11], vertex operator algebra and quantum field theory [a12], [a13], [a14], [a15]).
References
| [a1] | A.B. Venkov, "Spectral theory of automorphic functions" , Kluwer Acad. Publ. (1990) MR1135112 Zbl 0719.11030 |
| [a2] | J. Lehner, "Discontinuous groups and automorphic functions" , Amer. Math. Soc. (1964) MR0164033 Zbl 0178.42902 |
| [a3] | H. Weber, "Lehrbuch der Algebra" , Chelsea (1961) Zbl 48.0074.04 Zbl 43.0143.01 Zbl 30.0093.01 Zbl 29.0064.01 Zbl 39.0508.06 Zbl 27.0056.01 Zbl 26.0102.01 |
| [a4] | G. Shimura, "Complex multiplication in terms of elliptic curves" , Lecture Notes in Mathematics , 320 , Springer (1973) |
| [a5] | H. Stark, "Complex multiplication" , Lecture Notes in Mathematics , 320 , Springer (1973) |
| [a6] | D. Zagier, "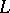 -series and the Green functions of modular curves" , Proc. Internat. Congress Mathematicians, Berkeley , Amer. Math. Soc. (1986) pp. 689–698 MR0934271 Zbl 0684.14005 -series and the Green functions of modular curves" , Proc. Internat. Congress Mathematicians, Berkeley , Amer. Math. Soc. (1986) pp. 689–698 MR0934271 Zbl 0684.14005 |
| [a7] | A.O.L. Atkin, H.P.P. Swinnerton-Dyer, "Modular forms on non-congruence subgroups" , Proc. Symp. Pure Math. , 19 , Amer. Math. Soc. (1971) pp. 1–26 MR337781 |
| [a8] | J.G. Thompson, "Finite groups and modular functions" Bull. London Math. Soc. , 11 (1979) pp. 347–351 MR0554401 Zbl 0424.20011 |
| [a9] | J.H. Conway, S.P. Norton, "Monstrous moonshine" Bull. London Math. Soc. , 11 (1979) pp. 308–339 MR0554399 Zbl 0424.20010 |
| [a10] | M. Koike, "Moonshine: a mysterious relationship between simple groups and automorphic functions" Amer. Math. Soc. Transl. Ser. 2 , 160 (1994) pp. 33–45 MR1308539 Zbl 0829.11025 |
| [a11] | R.E. Borchereds, "Sporadic groups and string theory" , First European Congress of Math. , 1 (1992) pp. 411–421 |
| [a12] | I.B. Frenkel, J. Lepowsky, A. Meurman, "Vertex operator algebras and the monster" , Acad. Press (1988) MR0996026 Zbl 0674.17001 |
| [a13] | E. Verlinde, H. Verlinde, "Chiral bosonization,determinants,and the string partition function" Nucl. Phys. , B288 (1987) pp. 357 MR0896667 |
| [a14] | D.J. Smit, "String theory and the algebraic geometry of moduli spaces" Comm. Math. Phys. , 114 (1988) pp. 645 MR929134 |
| [a15] | E. Witten, "Elliptic genera and quantum field theory" Comm. Math. Phys. , 109 (1987) pp. 525–536 MR0885560 Zbl 0625.57008 |
Gamma-invariant in the theory of modular forms. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gamma-invariant_in_the_theory_of_modular_forms&oldid=40962