Gamma-function
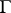 -function
-function
A transcendental function 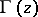 that extends the values of the factorial
that extends the values of the factorial 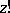 to any complex number
to any complex number 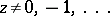 . It was introduced in 1729 by L. Euler in a letter to Ch. Goldbach, using the infinite product
. It was introduced in 1729 by L. Euler in a letter to Ch. Goldbach, using the infinite product
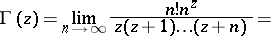 |
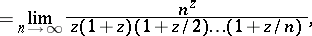 |
which was used by L. Euler to obtain the integral representation (Euler integral of the second kind, cf. Euler integrals)
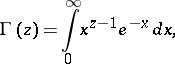 |
which is valid for 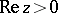 . The multi-valuedness of the function
. The multi-valuedness of the function 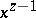 is eliminated by the formula
is eliminated by the formula 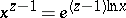 with a real
with a real 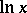 . The symbol
. The symbol 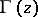 and the name gamma-function were proposed in 1814 by A.M. Legendre.
and the name gamma-function were proposed in 1814 by A.M. Legendre.
If  and
and 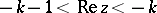 ,
, 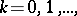 the gamma-function may be represented by the Cauchy–Saalschütz integral:
the gamma-function may be represented by the Cauchy–Saalschütz integral:
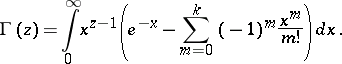 |
In the entire plane punctured at the points 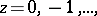 the gamma-function satisfies a Hankel integral representation:
the gamma-function satisfies a Hankel integral representation:
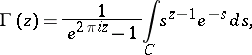 |
where 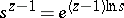 and
and 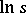 is the branch of the logarithm for which
is the branch of the logarithm for which 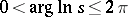 ; the contour
; the contour 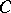 is represented in Fig. a. It is seen from the Hankel representation that
is represented in Fig. a. It is seen from the Hankel representation that 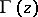 is a meromorphic function. At the points
is a meromorphic function. At the points 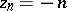 ,
, 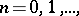 it has simple poles with residues
it has simple poles with residues 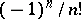 .
.
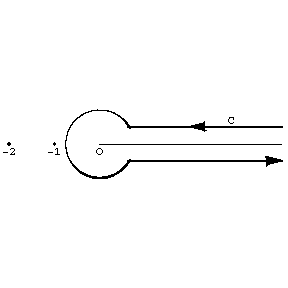
Figure: g043310a
Fundamental relations and properties of the gamma-function.
1) Euler's functional equation:
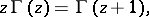 |
or
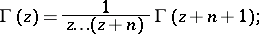 |
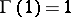 ,
, 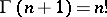 if
if 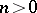 is an integer; it is assumed that
is an integer; it is assumed that 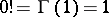 .
.
2) Euler's completion formula:
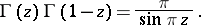 |
In particular, 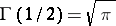 ;
;
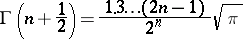 |
if 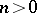 is an integer;
is an integer;
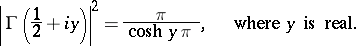 |
3) Gauss' multiplication formula:
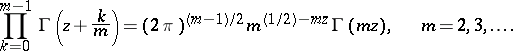 |
If 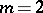 , this is the Legendre duplication formula.
, this is the Legendre duplication formula.
4) If  or
or 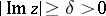 , then
, then 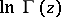 can be asymptotically expanded into the Stirling series:
can be asymptotically expanded into the Stirling series:
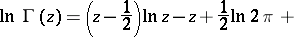 |
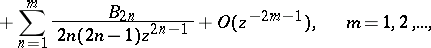 |
where 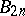 are the Bernoulli numbers. It implies the equality
are the Bernoulli numbers. It implies the equality
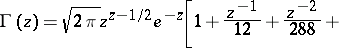 |
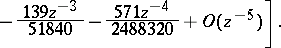 |
In particular,
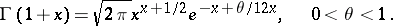 |
More accurate is Sonin's formula [6]:
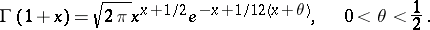 |
5) In the real domain, 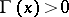 for
for 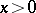 and it assumes the sign
and it assumes the sign  on the segments
on the segments 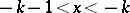 ,
, 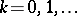 (Fig. b).
(Fig. b).
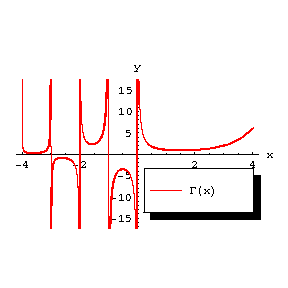
Figure: g043310b
The graph of the function  .
.
For all real  the inequality
the inequality
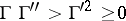 |
is valid, i.e. all branches of both  and
and 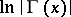 are convex functions. The property of logarithmic convexity defines the gamma-function among all solutions of the functional equation
are convex functions. The property of logarithmic convexity defines the gamma-function among all solutions of the functional equation
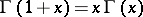 |
up to a constant factor.
For positive values of  the gamma-function has a unique minimum at
the gamma-function has a unique minimum at 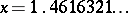 equal to
equal to 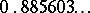 . The local minima of the function
. The local minima of the function 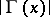 form a sequence tending to zero as
form a sequence tending to zero as 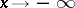 .
.
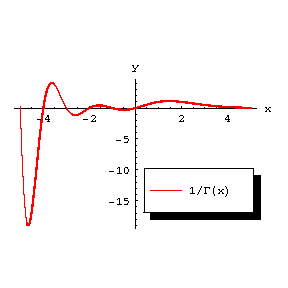
Figure: g043310c
The graph of the function 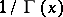 .
.
6) In the complex domain, if 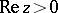 , the gamma-function rapidly decreases as
, the gamma-function rapidly decreases as 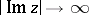 ,
,
 |
7) The function 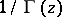 (Fig. c) is an entire function of order one and of maximal type; asymptotically, as
(Fig. c) is an entire function of order one and of maximal type; asymptotically, as  ,
,
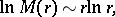 |
where
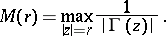 |
It can be represented by the infinite Weierstrass product:
 |
which converges absolutely and uniformly on any compact set in the complex plane (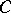 is the Euler constant). A Hankel integral representation is valid:
is the Euler constant). A Hankel integral representation is valid:
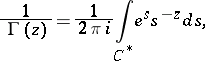 |
where the contour 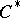 is shown in Fig. d.
is shown in Fig. d.
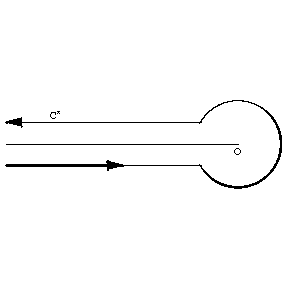
Figure: g043310d

G.F. Voronoi [7] obtained integral representations for powers of the gamma-function.
In applications, the so-called poly gamma-functions — 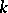 -th derivatives of
-th derivatives of 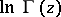 — are of importance. The function (Gauss'
— are of importance. The function (Gauss' 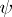 -function)
-function)
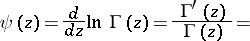 |
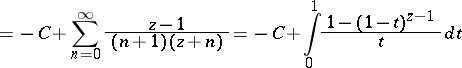 |
is meromorphic, has simple poles at the points 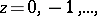 and satisfies the functional equation
and satisfies the functional equation
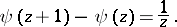 |
The representation of 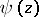 for
for 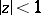 yields the formula
yields the formula
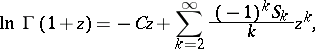 |
where
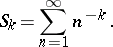 |
This formula may be used to compute 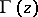 in a neighbourhood of the point
in a neighbourhood of the point 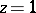 .
.
For other poly gamma-functions see [2]. The incomplete gamma-function is defined by the equation
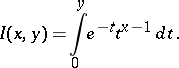 |
The functions 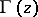 and
and 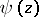 are transcendental functions which do not satisfy any linear differential equation with rational coefficients (Hölder's theorem).
are transcendental functions which do not satisfy any linear differential equation with rational coefficients (Hölder's theorem).
The exceptional importance of the gamma-function in mathematical analysis is due to the fact that it can be used to express a large number of definite integrals, infinite products and sums of series (see, for example, Beta-function). In addition, it is widely used in the theory of special functions (the hypergeometric function, of which the gamma-function is a limit case, cylinder functions, etc.), in analytic number theory, etc.
References
| [1] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) |
| [2] | H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 1. The gamma function. The hypergeometric functions. Legendre functions , McGraw-Hill (1953) |
| [3] | N. Bourbaki, "Elements of mathematics. Functions of a real variable" , Addison-Wesley (1976) (Translated from French) |
| [4] | , Math. anal., functions, limits, series, continued fractions , Handbook Math. Libraries , Moscow (1961) (In Russian) |
| [5] | N. Nielsen, "Handbuch der Theorie der Gammafunktion" , Chelsea, reprint (1965) |
| [6] | N.Ya. Sonin, "Studies on cylinder functions and special polynomials" , Moscow (1954) (In Russian) |
| [7] | G.F. Voronoi, "Studies of primitive parallelotopes" , Collected works , 2 , Kiev (1952) pp. 239–368 (In Russian) |
| [8] | E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German) |
| [9] | A. Angot, "Compléments de mathématiques. A l'usage des ingénieurs de l'electrotechnique et des télécommunications" , C.N.E.T. (1957) |
Comments
The 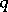 -analogue of the gamma-function is given by
-analogue of the gamma-function is given by
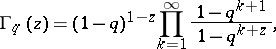 |
 |
cf. [a2]. Its origin goes back to E. Heine (1847) and D. Jackson (1904). For the gamma-function see also [a1].
References
| [a1] | E. Artin, "The gamma function" , Holt, Rinehart & Winston (1964) |
| [a2] | R. Askey, "The 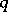 -Gamma and -Gamma and 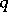 -Beta functions" Appl. Anal. , 8 (1978) pp. 125–141 -Beta functions" Appl. Anal. , 8 (1978) pp. 125–141 |
Gamma-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gamma-function&oldid=16735