Difference between revisions of "Gamma-function"
(→Fundamental relations and properties of the gamma-function.: added reference to Entire function) |
m (→Fundamental relations and properties of the gamma-function.: case fixes) |
||
| Line 107: | Line 107: | ||
<span id="Fig2"> | <span id="Fig2"> | ||
| − | [[File:Gamma-function-2.png| right| frame| Figure 2. The | + | [[File:Gamma-function-2.png| right| frame| Figure 2. The gamma function on the real line ([[Media:Gamma-function-2.pdf|pdf]]) ]] |
</span> | </span> | ||
5) In the real | 5) In the real | ||
| Line 165: | Line 165: | ||
G.F. Voronoi {{Cite|Vo}} obtained integral representations for powers of the gamma-function. | G.F. Voronoi {{Cite|Vo}} obtained integral representations for powers of the gamma-function. | ||
| − | In applications, the so-called poly gamma | + | In applications, the so-called poly-gamma functions — $k$th derivatives of $\ln\Gamma(z)$ — are of importance. The function (Gauss' $\psi$-function) |
$$ | $$ | ||
\psi(z) = | \psi(z) = | ||
| Line 194: | Line 194: | ||
The functions $\Gamma(z)$ and $\psi(z)$ are transcendental functions which do not satisfy any linear differential equation with rational coefficients (Hölder's theorem). | The functions $\Gamma(z)$ and $\psi(z)$ are transcendental functions which do not satisfy any linear differential equation with rational coefficients (Hölder's theorem). | ||
| − | The exceptional importance of the gamma-function in mathematical analysis is due to the fact that it can be used to express a large number of definite integrals, infinite products and sums of series ( | + | The exceptional importance of the gamma-function in mathematical analysis is due to the fact that it can be used to express a large number of definite integrals, infinite products and sums of series (for example, the [[Beta-function|beta-function]]). In addition, it is widely used in the theory of special functions (the [[Hypergeometric function|hypergeometric function]], of which the gamma-function is a limit case, [[Cylinder functions|cylinder functions]], etc.), in analytic number theory, etc. |
====References==== | ====References==== | ||
Revision as of 00:11, 29 April 2012
$\Gamma$-function
2020 Mathematics Subject Classification: Primary: 33B15 Secondary: 33B2033D05 [MSN][ZBL] $ \newcommand{\abs}[1]{\left|#1\right|} \newcommand{\Re}{\mathop{\mathrm{Re}}} \newcommand{\Im}{\mathop{\mathrm{Im}}} $
A transcendental function $\Gamma(z)$ that extends the values of the factorial $z!$ to any complex number $z$. It was introduced in 1729 by L. Euler in a letter to Ch. Goldbach, using the infinite product $$ \Gamma(z) = \lim_{n\rightarrow\infty}\frac{n!n^z}{z(z+1)\ldots(z+n)} = \lim_{n\rightarrow\infty}\frac{n^z}{z(1+z/2)\ldots(1+z/n)}, $$ which was used by L. Euler to obtain the integral representation (Euler integral of the second kind, cf. Euler integrals) $$ \Gamma(z) = \int_0^\infty x^{z-1}e^{-x} \rd x, $$ which is valid for $\Re z > 0$. The multi-valuedness of the function $x^{z-1}$ is eliminated by the formula $x^{z-1}=e^{(z-1)\ln x}$ with a real $\ln x$. The symbol $\Gamma(z)$ and the name gamma-function were proposed in 1814 by A.M. Legendre.
If $\Re z < 0$ and $-k-1 < \Re z < -k$, $k=0,1,\ldots$, the gamma-function may be represented by the Cauchy–Saalschütz integral: $$ \Gamma(z) = \int_0^\infty x^{z-1} \left( e^{-x} - \sum_{m=0}^k (-1)^m \frac{x^m}{m!} \right) \rd x. $$ In the entire plane punctured at the points $z=0,-1,\ldots $, the gamma-function satisfies a Hankel integral representation: \begin{equation} \label{eq1} \Gamma(z) = \frac{1}{e^{2\pi iz} - 1} \int_C s^{z-1}e^{-s} \rd s, \end{equation} where $s^{z-1} = e^{(z-1)\ln s}$ and $\ln s$ is the branch of the logarithm for which $0 < \arg\ln s < 2\pi$; the contour $C$ is represented in Figure 1. It is seen from the Hankel representation that $\Gamma(z)$ is a meromorphic function. At the points $z_n = -n$, $n=0,1,\ldots$ it has simple poles with residues $(-1)^n/n!$.
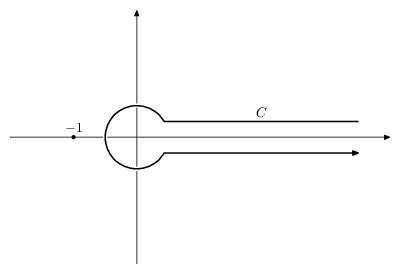
Fundamental relations and properties of the gamma-function.
1) Euler's functional equation: $$ z\Gamma(z) = \Gamma(z+1), $$ or $$ \Gamma(z) = \frac{1}{z\ldots(z+n)}\Gamma(z+n+1); $$ $\Gamma(1)=1$, $\Gamma(n+1) = n!$ if $n$ is an integer; it is assumed that $0! = \Gamma(1) = 1$.
2) Euler's completion formula: $$ \Gamma(z)\Gamma(1-z) = \frac{\pi}{\sin \pi z}. $$ In particular, $\Gamma(1/2)=\sqrt{\pi}$; $$ \Gamma\left(n+\frac{1}{2}\right) = \frac{1.3\ldots(2n-1)}{2^n}\sqrt{\pi} $$ if $n>0$ is an integer; $$ \abs{\Gamma\left(\frac{1}{2} + iy\right)}^2 = \frac{\pi}{\cosh y\pi}, $$ where $y$ is real.
3) Gauss' multiplication formula: $$ \prod_{k=0}^{m-1} \Gamma\left( z + \frac{k}{m} \right) = (2\pi)^{(m-1)/2}m^{(1/2)-mz}\Gamma(mz), \quad m = 2,3,\ldots $$ If $m=2$, this is the Legendre duplication formula.
4) If $\Re z \geq \delta > 0$ or $\abs{\Im z} \geq \delta > 0$, then $\ln\Gamma(z)$ can be asymptotically expanded into the Stirling series: $$ \ln\Gamma(z) = \left(z-\frac{1}{2}\right)\ln z - z + \frac{1}{2}\ln 2\pi + \sum_{n=1}^m \frac{B_{2n}}{2n(2n-1)z^{2n-1}} + O\bigl(z^{-2m-1}\bigr), \quad m = 1,2,\ldots, $$ where $B_{2n}$ are the Bernoulli numbers. It implies the equality $$ \Gamma(z) = \sqrt{2\pi} z^{z-1/2} z^{-z} \left( 1 + \frac{1}{12}z^{-1} + \frac{1}{288}z^{-2} - \frac{139}{51840}z^{-3} - \frac{571}{2488320}z^{-4} + O\bigl(z^{-5}\bigr) \right). $$ In particular, $$ \Gamma(1+x) = \sqrt{2\pi} x^{x+1/2} e^{-x + \theta/12x}, \quad 0 < \theta < 1. $$ More accurate is Sonin's formula [So]: $$ \Gamma(1+x) = \sqrt{2\pi} x^{x+1/2} e^{-x + 1/12(x+\theta)}, \quad 0 < \theta < 1/2. $$

5) In the real domain, $\Gamma(x) > 0$ for $x > 0$ and it assumes the sign $(-1)^{k+1}$ on the segments $-k-1 < x < -k$, $k = 0,1,\ldots$ (Figure 2).
For all real $x$ the inequality $$ \Gamma\Gamma^{\prime\prime} > \bigl(\Gamma^\prime\bigr)^2 \geq 0 $$ is valid, i.e. all branches of both $\abs{\Gamma(x)}$ and $\ln\abs{\Gamma(x)}$ are convex functions. The property of logarithmic convexity defines the gamma-function among all solutions of the functional equation $$ \Gamma(1+x) = x\Gamma(x) $$ up to a constant factor (see also the Bohr–Mollerup theorem).
For positive values of $x$ the gamma-function has a unique minimum at $x=1.4616321\ldots$ equal to $0.885603\ldots$. The local minima of the function $\abs{\Gamma(x)}$ form a sequence tending to zero as $x\rightarrow -\infty$.
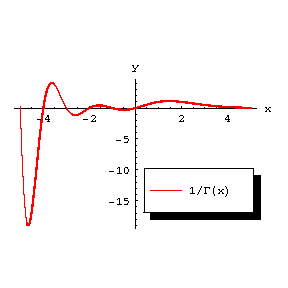
Figure: g043310c
The graph of the function $ $.
6) In the complex domain, if $\Re z > 0$, the gamma-function rapidly decreases as $\abs{\Im z} \rightarrow \infty$, $$ \lim_{\abs{\Im z} \rightarrow \infty} \abs{\Gamma(z)}\abs{\Im z}^{(1/2)-\Re z}e^{\pi\abs{\Im z}/2} = \sqrt{2\pi}. $$
7) The function $1/\Gamma(z)$ (Fig. c) is an entire function of order one and of maximal type; asymptotically, as $r \rightarrow \infty$, $$ \ln M(r) \sim r \ln r, $$ where $$ M(r) = \max_{\abs{z} = r} \frac{1}{\abs{\Gamma(z)}}. $$ It can be represented by the infinite Weierstrass product: $$ \frac{1}{\Gamma(z)} = z e^{\gamma z} \prod_{n=1}^\infty \left(\left( 1 + \frac{z}{n} \right) e^{-z/n} \right), $$ which converges absolutely and uniformly on any compact set in the complex plane ($\gamma$ is the Euler constant). A Hankel integral representation is valid: $$ \frac{1}{\Gamma(z)} = \frac{1}{2\pi i} \int_{C'} e^s s^{-z} \rd s, $$ where the contour $C'$ is shown in Fig. d.
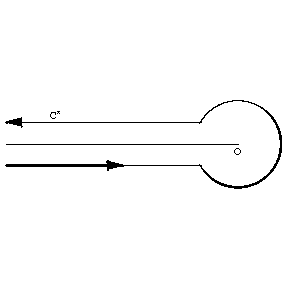
Figure: g043310d
$ $
G.F. Voronoi [Vo] obtained integral representations for powers of the gamma-function.
In applications, the so-called poly-gamma functions — $k$th derivatives of $\ln\Gamma(z)$ — are of importance. The function (Gauss' $\psi$-function) $$ \psi(z) = \frac{\mathrm{d}}{\mathrm{d}z}\ln\Gamma(z) = \frac{\Gamma'(z)}{\Gamma(z)} = -\gamma + \sum_{n=0}^\infty \frac{z-1}{(n+1)(z+n)} = -\gamma + \int_0^1 \frac{1 - (1-t)^{z-1}}{t} \rd t $$ is meromorphic, has simple poles at the points $z=0,-1,\ldots$ and satisfies the functional equation $$ \psi(z+1) - \psi(z) = \frac{1}{z}. $$ The representation of $\psi(z)$ for $\abs{z}<1$ yields the formula $$ \ln\Gamma(1+z) = -\gamma z + \sum_{k=2}^\infty \frac{(-1)^k S_k}{k} z^k, $$ where $$ S_k = \sum_{n=1}^\infty n^{-k}. $$ This formula may be used to compute $\Gamma(z)$ in a neighbourhood of the point $z=1$.
For other poly gamma-functions see [BaEr]. The incomplete gamma-function is defined by the equation $$ I(x,y) = \int_0^y e^{-t}t^{x-1} \rd t. $$ The functions $\Gamma(z)$ and $\psi(z)$ are transcendental functions which do not satisfy any linear differential equation with rational coefficients (Hölder's theorem).
The exceptional importance of the gamma-function in mathematical analysis is due to the fact that it can be used to express a large number of definite integrals, infinite products and sums of series (for example, the beta-function). In addition, it is widely used in the theory of special functions (the hypergeometric function, of which the gamma-function is a limit case, cylinder functions, etc.), in analytic number theory, etc.
References
| [An] | A. Angot, "Compléments de mathématiques. A l'usage des ingénieurs de l'electrotechnique et des télécommunications", C.N.E.T. (1957) |
| [BaEr] | H. Bateman (ed.) A. Erdélyi (ed.), Higher transcendental functions, 1. The gamma function. The hypergeometric functions. Legendre functions, McGraw-Hill (1953) |
| [Bo] | N. Bourbaki, "Elements of mathematics. Functions of a real variable", Addison-Wesley (1976) (Translated from French) |
| [JaEm] | E. Jahnke, F. Emde, "Tables of functions with formulae and curves", Dover, reprint (1945) (Translated from German) |
| [Ni] | N. Nielsen, "Handbuch der Theorie der Gammafunktion", Chelsea, reprint (1965) |
| [So] | N.Ya. Sonin, "Studies on cylinder functions and special polynomials", Moscow (1954) (In Russian) |
| [Vo] | G.F. Voronoi, "Studies of primitive parallelotopes", Collected works, 2, Kiev (1952) pp. 239–368 (In Russian) |
| [WhWa] | E.T. Whittaker, G.N. Watson, "A course of modern analysis", Cambridge Univ. Press (1952) |
Comments
For an approach to the gamma-function based on the Bohr–Mollerup characterization, see the short monograph by E. Artin [Ar].
The $q$-analogue of the gamma-function is given by $$ \Gamma_q(z) = (1-q)^{1-z} \prod_{k=1}^\infty \frac{1-q^{k+1}}{1-q^{k+z}}, \quad z \neq 0,-1,-2,\ldots;\quad 0<q<1, $$ cf. [As]. Its origin goes back to E. Heine (1847) and D. Jackson (1904).
References
| [Ar] | E. Artin, "The gamma function", Holt, Rinehart & Winston (1964) |
| [As] | R. Askey, "The $q$-Gamma and $q$-Beta functions" Appl. Anal., 8 (1978) pp. 125–141 |
Gamma-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gamma-function&oldid=25680