Galois theory
In the most general sense it is a theory dealing with mathematical objects on the basis of their automorphism groups. For instance, Galois theories of fields, rings, topological spaces, etc., are possible. In a narrower sense Galois theory is the Galois theory of fields. The theory originated in the context of finding roots of algebraic equations of high degrees. The familiar formula for solving equations of degree two dates back to early Antiquity. Methods for solving cubic (cf. Cardano formula) and quartic (cf. Ferrari method) equations were discovered in the 16th century. Unsuccessful attempts to find formulas for solving quintic and higher-degree equations were made during the three centuries which followed. It was finally proved by N.H. Abel in 1824 that there are no solutions in radicals of the general equation of degree 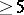 . The next problem was to find necessary and sufficient conditions to be satisfied by the coefficients of an equation for the latter to be solvable in radicals, i.e. for it to be reducible to a chain of two-term equations of the form
. The next problem was to find necessary and sufficient conditions to be satisfied by the coefficients of an equation for the latter to be solvable in radicals, i.e. for it to be reducible to a chain of two-term equations of the form 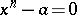 . This problem was solved by E. Galois; his results were exposed in a letter on the eve of his death (1832), and published in 1846. The theory of Galois will now be summarized in modern language.
. This problem was solved by E. Galois; his results were exposed in a letter on the eve of his death (1832), and published in 1846. The theory of Galois will now be summarized in modern language.
Let 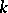 be an arbitrary field. An extension of
be an arbitrary field. An extension of 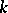 is any field
is any field 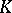 that contains
that contains 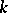 as a subfield. Any extension may be regarded as a linear space over
as a subfield. Any extension may be regarded as a linear space over 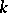 ; if this space has finite dimension
; if this space has finite dimension  , the extension is called finite, while the dimension
, the extension is called finite, while the dimension  is called the degree of the extension. An element
is called the degree of the extension. An element 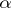 of an extension of
of an extension of 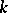 is said to be algebraic over
is said to be algebraic over 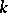 if it is the root of an equation
if it is the root of an equation 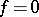 , where
, where 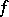 is a non-zero polynomial with coefficients from
is a non-zero polynomial with coefficients from 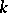 (this polynomial may be taken to be irreducible). The smallest extension of
(this polynomial may be taken to be irreducible). The smallest extension of 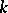 containing the algebraic element
containing the algebraic element 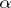 over
over 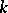 is usually denoted by
is usually denoted by 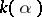 . A finite extension
. A finite extension 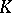 of
of  is called separable if
is called separable if 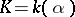 and if the irreducible polynomial
and if the irreducible polynomial 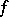 with
with 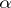 as a root has no multiple roots. If the characteristic of
as a root has no multiple roots. If the characteristic of 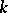 is zero (e.g. if
is zero (e.g. if 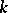 is a number field), any finite extension is separable (the theorem on the primitive element). The splitting field of an irreducible polynomial
is a number field), any finite extension is separable (the theorem on the primitive element). The splitting field of an irreducible polynomial 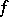 in
in 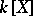 is the smallest extension of
is the smallest extension of  that contains all the roots of this polynomial. The degree of such an extension is divisible by the degree of
that contains all the roots of this polynomial. The degree of such an extension is divisible by the degree of 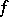 and is equal to it if all the roots of
and is equal to it if all the roots of 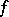 can be expressed as polynomials in one of them. An extension
can be expressed as polynomials in one of them. An extension 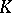 of
of 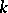 is called normal if it is the splitting field of a certain polynomial in
is called normal if it is the splitting field of a certain polynomial in 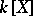 , and is called a Galois extension if it is normal and separable. The group of all automorphisms of a Galois extension
, and is called a Galois extension if it is normal and separable. The group of all automorphisms of a Galois extension 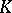 that leave all elements of
that leave all elements of 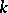 invariant is called the Galois group of this extension and is denoted by
invariant is called the Galois group of this extension and is denoted by 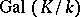 . Its order (the number of elements) is equal to the degree of
. Its order (the number of elements) is equal to the degree of 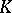 over
over 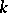 . To each subgroup
. To each subgroup 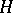 of
of 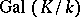 corresponds a subfield
corresponds a subfield 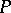 of
of 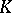 , consisting of all elements from
, consisting of all elements from 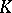 that remain fixed under all automorphisms from
that remain fixed under all automorphisms from 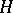 . Conversely, to each subfield
. Conversely, to each subfield 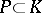 that contains
that contains 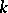 corresponds a subgroup
corresponds a subgroup 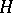 of
of 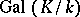 . It consists of all automorphisms leaving each element of
. It consists of all automorphisms leaving each element of 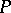 invariant. Here,
invariant. Here, 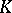 is a Galois extension of
is a Galois extension of 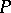 and
and 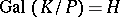 . The main theorem in Galois theory states that these correspondences are mutually inverse, and are therefore one-to-one correspondences between all subgroups of
. The main theorem in Galois theory states that these correspondences are mutually inverse, and are therefore one-to-one correspondences between all subgroups of 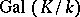 and all subfields of
and all subfields of 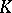 containing
containing 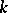 . Thus, the description of all subfields of
. Thus, the description of all subfields of 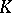 is reduced to the description of all subgroups of the finite group
is reduced to the description of all subgroups of the finite group 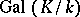 , which is a much simpler task. It is important to note that in this correspondence certain "good" properties of subgroups correspond to the "good" properties of subfields and vice versa. Thus, a subgroup
, which is a much simpler task. It is important to note that in this correspondence certain "good" properties of subgroups correspond to the "good" properties of subfields and vice versa. Thus, a subgroup 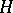 will be a normal subgroup of
will be a normal subgroup of 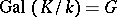 if and only if the field
if and only if the field 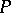 which corresponds to it is a Galois extension of
which corresponds to it is a Galois extension of 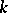 . Moreover,
. Moreover, 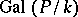 is isomorphic to
is isomorphic to  . To each ascending chain
. To each ascending chain
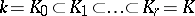 | (1) |
of subfields of 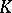 corresponds a descending chain
corresponds a descending chain
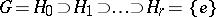 | (2) |
of subgroups of 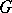 , where
, where 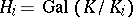 . The chain (2) is a normal series (i.e. each group
. The chain (2) is a normal series (i.e. each group 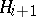 is a normal subgroup of
is a normal subgroup of 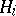 if
if 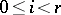 ) if and only if each field
) if and only if each field  in the chain (1) is a Galois extension of
in the chain (1) is a Galois extension of 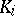 , and in this a case one has
, and in this a case one has 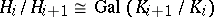 .
.
These results are applied to the solution of algebraic equations as follows. Let 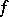 be an irreducible polynomial without multiple roots over the field
be an irreducible polynomial without multiple roots over the field 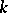 and let
and let 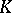 be its splitting field (which will be a Galois extension of
be its splitting field (which will be a Galois extension of 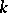 ). The Galois group of this extension is called the Galois group of the equation
). The Galois group of this extension is called the Galois group of the equation 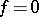 . Solving the equation
. Solving the equation 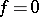 is reduced to solving a chain of equations
is reduced to solving a chain of equations 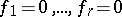 if and only if
if and only if 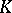 is contained in a field
is contained in a field 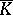 that is the last term of the ascending chain of fields
that is the last term of the ascending chain of fields
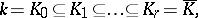 |
where 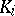 ,
, 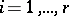 , is the splitting field of
, is the splitting field of 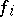 over
over 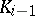 . This last condition is equivalent with the group
. This last condition is equivalent with the group 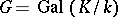 being a quotient group of the group
being a quotient group of the group 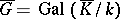 with a normal series whose factors
with a normal series whose factors 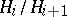 are isomorphic to the Galois groups of the equations
are isomorphic to the Galois groups of the equations 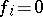 over
over 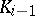 .
.
Let the field 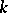 contain all roots of unity of order
contain all roots of unity of order  . Then, for any
. Then, for any 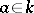 , the splitting field of the polynomial
, the splitting field of the polynomial 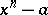 is
is 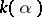 , where
, where 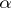 is one of the values of the radical
is one of the values of the radical 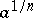 . In such a case
. In such a case 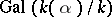 is a cyclic group of order dividing
is a cyclic group of order dividing  ; conversely, if
; conversely, if 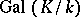 is a cyclic group of order
is a cyclic group of order  , one has
, one has 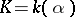 , where
, where 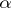 is the root of some two-term equation
is the root of some two-term equation 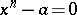 . Thus, if
. Thus, if 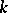 contains the roots of unity of all possible orders, then the equation
contains the roots of unity of all possible orders, then the equation 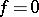 is solvable in radicals if and only if its Galois group is solvable (i.e. has a normal series with cyclic factors
is solvable in radicals if and only if its Galois group is solvable (i.e. has a normal series with cyclic factors 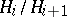 ). This condition of solvability in radicals is also valid if
). This condition of solvability in radicals is also valid if 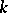 does not contain all possible roots of unity, since the Galois group
does not contain all possible roots of unity, since the Galois group 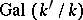 of the extension
of the extension 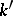 which is obtained by adjoining these roots is always solvable.
which is obtained by adjoining these roots is always solvable.
In practical applications of the solvability condition, a very important fact is that the Galois group of an equation can be computed without solving the equation itself. The idea of this computation can be stated as follows. Each automorphism of the splitting field of a polynomial 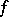 induces a permutation of its roots, and the automorphism is completely determined by this permutation. For this reason the Galois group of the equation may be treated, in principle, as a subgroup of the group of permutations of its roots (namely, the subgroup consisting of permutations that preserve all algebraic relations between the roots). The relations between the roots of a polynomial yield certain relations between its coefficients (by virtue of Viète's formulas); by analyzing these relations it is possible to determine the relations between the roots of the polynomial and thus to compute the Galois group of the equation. In the general case the Galois group of an algebraic equation consists of all permutations of the roots, i.e. is the symmetric group of degree
induces a permutation of its roots, and the automorphism is completely determined by this permutation. For this reason the Galois group of the equation may be treated, in principle, as a subgroup of the group of permutations of its roots (namely, the subgroup consisting of permutations that preserve all algebraic relations between the roots). The relations between the roots of a polynomial yield certain relations between its coefficients (by virtue of Viète's formulas); by analyzing these relations it is possible to determine the relations between the roots of the polynomial and thus to compute the Galois group of the equation. In the general case the Galois group of an algebraic equation consists of all permutations of the roots, i.e. is the symmetric group of degree  . Since a symmetric group is unsolvable for
. Since a symmetric group is unsolvable for 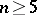 , there are, generally speaking, no solutions in radicals of quintic equations and equations of a higher degree (Abel's theorem).
, there are, generally speaking, no solutions in radicals of quintic equations and equations of a higher degree (Abel's theorem).
The ideas of Galois theory permit, in particular, to give a complete description of the class of construction problems that are solvable by ruler and compass. It is possible to show by methods of analytic geometry that any such construction problem can be reduced to some algebraic equation over the field of rational numbers, and the problem is solvable by using a ruler and compass if and only if the corresponding equation is solvable in quadratic radicals. This is the case if and only if the Galois group of the equation has a normal series whose factors are groups of order two, and this occurs if and only if its order is a power of two. Thus, a construction problem solvable by ruler and compass is reduced to solving an equation whose splitting field has degree 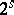 over the field of rational numbers for some
over the field of rational numbers for some  ; if the degree of the equation is not of the form
; if the degree of the equation is not of the form 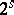 , such a construction is impossible. This is the case for the problem of doubling the cube (which leads to the cubic equation
, such a construction is impossible. This is the case for the problem of doubling the cube (which leads to the cubic equation 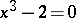 ) and for the problem of trisecting a given angle (which also leads to a cubic equation). If
) and for the problem of trisecting a given angle (which also leads to a cubic equation). If 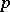 is a prime number, the problem of constructing a regular
is a prime number, the problem of constructing a regular 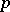 -gon leads to the equation
-gon leads to the equation 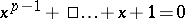 , whose splitting field is generated by any root and is therefore of degree
, whose splitting field is generated by any root and is therefore of degree 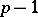 , the degree of the equation. In this case a ruler-and-compass construction is possible if and only if
, the degree of the equation. In this case a ruler-and-compass construction is possible if and only if 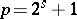 (e.g. if
(e.g. if 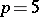 and
and 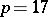 it is possible, but is not possible for
it is possible, but is not possible for 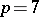 or
or 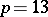 ).
).
The ideas of Galois had a decisive influence on the development of algebra during almost a whole century. Galois theory was extended and generalized in many directions. W. Krull developed a Galois theory for infinite extensions (cf. Galois topological group); it was proved (the Kronecker–Weber theorem) that the roots of an equation with rational coefficients and with an Abelian Galois group are rational linear combinations of roots of unity; a classification of the Abelian extensions of a given algebraic number field (class field theory) was given; a proof was given for the existence of an algebraic number field with given solvable Galois group over the field of rational numbers (cf. Galois theory, inverse problem of). Nevertheless, classical Galois theory still contains many unsolved problems. For instance, it is not known whether any finite group occurs as the Galois group of an equation over the field of rational numbers.
References
| [1] | E. Galois, "Écrits et mémoires d'E. Galois" , Gauthier-Villars (1962) |
| [2] | N.G. [N.G. Chebotarev] Tschebotaröw, "Grundzüge der Galois'schen Theorie" , Noordhoff (1950) (Translated from Russian) |
| [3] | N.G. Chebotarev, "Galois theory" , Moscow-Leningrad (1936) (In Russian) |
| [4] | M.M. Postnikov, "Fundamentals of Galois theory" , Noordhoff (1962) (Translated from Russian) |
| [5] | M.M. Postnikov, "Fundamentals of Galois theory" , Noordhoff (1962) (Translated from Russian) |
| [6] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [7] | S. Lang, "Algebra" , Addison-Wesley (1974) |
| [8] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) |
| [9] | H. Koch, "Galoissche Theorie der 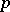 -Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970) -Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970) |
| [10] | E. Artin, "Galois theory" , Notre Dame Univ. , Indiana (1948) |
Galois theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galois_theory&oldid=17535