Difference between revisions of "Galois cohomology"
Ulf Rehmann (talk | contribs) |
Ulf Rehmann (talk | contribs) |
||
| Line 1: | Line 1: | ||
| − | Cohomology of a [[Galois group|Galois group]]. Let < | + | Cohomology of a [[Galois group|Galois group]]. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g0431001.png" /> be an Abelian group, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g0431002.png" /> be the Galois group of an extension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g0431003.png" /> and suppose <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g0431004.png" /> acts on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g0431005.png" />; the Galois cohomology groups will then be the cohomology groups |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | be | ||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g0431006.png" /></td> </tr></table> | |
| − | |||
| − | < | ||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | </ | ||
| − | < | ||
| − | |||
| − | |||
| − | + | defined by the complex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g0431007.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g0431008.png" /> consists of all mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g0431009.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310010.png" /> is the coboundary operator (cf. [[Cohomology of groups|Cohomology of groups]]). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310011.png" /> is an extension of infinite degree, an additional requirement is that the [[Galois topological group|Galois topological group]] acts continuously on the discrete group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310012.png" />, and continuous mappings are taken for the cochains in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310013.png" />. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[ | ||
| − | + | Usually, only zero-dimensional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310014.png" /> and one-dimensional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310015.png" /> cohomology are defined for a non-Abelian group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310016.png" />. Namely, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310017.png" /> is the set of fixed points under the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310018.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310019.png" />, while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310020.png" /> is the quotient set of the set of one-dimensional cocycles, i.e. continuous mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310021.png" /> that satisfy the relation | |
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | of the | ||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310022.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | </ | ||
| − | + | for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310023.png" />, by the equivalence relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310024.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310025.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310026.png" /> for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310027.png" /> and all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310028.png" />. In the non-Abelian case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310029.png" /> is a set with a distinguished point corresponding to the trivial cocycle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310030.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310031.png" /> is the unit of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310032.png" />, and usually has no group structure. Nevertheless, a standard cohomology formalism can be developed for such cohomology as well (cf. [[Non-Abelian cohomology|Non-Abelian cohomology]]). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | cohomology | ||
| − | |||
| − | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310033.png" /> is the separable closure of a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310034.png" />, it is customary to denote the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310035.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310036.png" />, and to write <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310037.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310038.png" />. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Galois cohomology groups were implicitly present in the work of D. Hilbert, E. Artin, R. Brauer, H. Hasse, and C. Chevalley on class field theory, finite-dimensional simple algebras and quadratic forms. The development of the ideas and methods of homological algebra resulted in the introduction of Galois cohomology groups of finite extensions with values in an Abelian group by E. Artin, A. Weil, G. Hochschild, and J. Tate in the 1950s, in connection with class field theory. The general theory of Abelian Galois cohomology groups was then developed by Tate and J.-P. Serre [[#References|[1]]], [[#References|[3]]], [[#References|[6]]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | H | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | group. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Tate used Galois cohomology to introduce the concept of the cohomological dimension of the Galois group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310039.png" /> of a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310040.png" /> (denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310041.png" />). It is defined in terms of the cohomological <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310043.png" />-dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310044.png" />, which is the smallest integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310045.png" /> such that for any torsion <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310046.png" />-module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310047.png" /> and any integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310048.png" /> the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310049.png" />-primary component of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310050.png" /> is zero. The cohomological dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310051.png" /> is | |
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | < | ||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310052.png" /></td> </tr></table> | |
| − | |||
| − | < | ||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | + | For any algebraically closed field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310053.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310054.png" />; for all fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310055.png" /> such that the [[Brauer group|Brauer group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310056.png" /> of an arbitrary extension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310057.png" /> is trivial, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310058.png" />; for the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310059.png" />-adic field, the field of algebraic functions of one variable over a finite field of constants and for a totally-complex number field, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310060.png" /> [[#References|[1]]]. Fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310061.png" /> whose Galois group has cohomological dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310062.png" /> and whose Brauer group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310063.png" /> are called fields of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310065.png" />; this is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310066.png" />. Such fields include all finite fields, maximal unramified extensions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310067.png" />-adic fields, and the field of rational functions in one variable over an algebraically closed field of constants. If a Galois group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310068.png" /> is a [[Pro-p group|pro-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310069.png" />-group]], i.e. is the projective limit of finite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310070.png" />-groups, the dimension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310071.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310072.png" /> is equal to the minimal number of topological generators of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310073.png" />, while the dimension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310074.png" /> is the number of defining relations between these generators. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310075.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310076.png" /> is a free pro-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310077.png" />-group. | |
| − | < | ||
| − | |||
| − | </ | ||
| − | < | ||
| − | |||
| − | </ | ||
| − | < | ||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | </ | ||
| − | include, | ||
| − | |||
| − | </ | ||
| − | fields. | ||
| − | < | ||
| − | |||
| − | </ | ||
| − | < | ||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | </ | ||
| − | + | Non-Abelian Galois cohomology appeared in the late 1950s, but systematic research began only in the 1960s, mainly in response to the need for the classification of algebraic groups over not algebraically closed fields. One of the principal problems which stimulated the development of non-Abelian Galois cohomology is the task of classifying principal homogeneous spaces of group schemes. Galois cohomology groups proved to be specially effective in the problem of classifying types of algebraic varieties. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | These problems led to the problem of computing the Galois cohomology groups of algebraic groups. The general theorems on the structure of algebraic groups essentially reduce the study of Galois cohomology groups to a separate consideration of the Galois cohomology groups of finite groups, unipotent groups, tori, semi-simple groups, and Abelian varieties. | |
| − | + | ||
| − | </ | + | The Galois cohomology groups of a connected unipotent group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310078.png" /> are trivial if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310079.png" /> is defined over a perfect field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310080.png" />, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310081.png" /> for an arbitrary unipotent group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310082.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310083.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310084.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310085.png" /> is an Abelian group. In particular, for the additive group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310086.png" /> of an arbitrary field one always has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310087.png" />. For an imperfect field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310088.png" />, in general <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310089.png" />. |
| − | + | ||
| − | + | One of the first significant facts about Galois cohomology groups was Hilbert's "Theorem 90" , one formulation of which states that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310090.png" /> (where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310091.png" /> is the multiplicative group). Moreover, for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310092.png" />-split algebraic torus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310093.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310094.png" />. The computation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310095.png" /> for an arbitrary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310096.png" />-defined torus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310097.png" /> can be reduced, in the general case, to the computation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310098.png" /> where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g04310099.png" /> is a Galois splitting field of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100100.png" />; so far (1989) this has only been accomplished for special fields. The case when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100101.png" /> is an algebraic number field is especially important in practical applications. Duality theorems, with various applications, have been developed for this case. | |
| − | </ | + | |
| − | non- | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100102.png" /> be a [[Galois extension|Galois extension]] of finite degree, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100103.png" /> be the group of adèles (cf. [[Adèle|Adèle]]) of a multiplicative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100104.png" />-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100105.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100106.png" /> be the group of characters of a torus. The duality theorem states that the cup-product |
| − | + | ||
| − | </ | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100107.png" /></td> </tr></table> |
| − | < | + | |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100108.png" /></td> </tr></table> | |
| − | </ | + | |
| − | of < | + | defines non-degenerate pairing for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100109.png" />. This theorem was used to find the formula for expressing the Tamagawa numbers (cf. [[Tamagawa number|Tamagawa number]]) of the torus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100110.png" /> by invariants connected with its Galois cohomology groups. Other important duality theorems for Galois cohomology groups also exist [[#References|[1]]]. |
| − | + | ||
| − | </ | + | It has been proved [[#References|[11]]] that the groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100111.png" /> over fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100112.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100113.png" /> are trivial. A natural class of fields has been distinguished with only a finite number of extensions of a given degree (the so-called type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100115.png" /> fields); these include, for example, the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100116.png" />-adic number fields. It was proved [[#References|[1]]] that for any algebraic group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100117.png" /> over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100118.png" /> of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100119.png" /> the cohomology group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100120.png" /> is a finite set. |
| − | + | ||
| − | + | The theory of Galois cohomology of semi-simple algebraic groups has far-reaching arithmetical and analytical applications. The Kneser–Bruhat–Tits theorem states that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100121.png" /> for simply-connected semi-simple algebraic groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100122.png" /> over local fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100123.png" /> whose residue field has cohomological dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100124.png" />. This theorem was first proved for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100125.png" />-adic number fields , after which a proof was obtained for the general case. It was proved | |
| − | </ | + | |
| − | < | + | that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100126.png" /> is trivial for a field of algebraic functions in one variable over a finite field of constants. In all these cases the cohomological dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100127.png" />, which confirms the general conjecture of Serre to the effect that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100128.png" /> is trivial for simply-connected semi-simple <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100129.png" /> over fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100130.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100131.png" />. |
| − | + | ||
| − | </ | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100132.png" /> be a global field, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100133.png" /> be the set of all non-equivalent valuations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100134.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100135.png" /> be the completion of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100136.png" />. The imbeddings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100137.png" /> induce a natural mapping |
| − | for an arbitrary algebraic group < | + | |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100138.png" /></td> </tr></table> | |
| − | + | ||
| − | + | for an arbitrary algebraic group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100139.png" /> defined over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100140.png" />, the kernel of which is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100141.png" /> and, in the case of Abelian varieties, is called the Tate–Shafarevich group. The group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100142.png" /> measures the extent to which the Galois cohomology groups over a global field are described by Galois cohomology groups over localizations. The principal result on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100143.png" /> for linear algebraic groups is due to A. Borel, who proved that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100144.png" /> is finite. There exists a conjecture according to which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100145.png" /> is finite in the case of Abelian varieties as well. The situation in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100146.png" />, i.e. the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100147.png" /> is injective, is a special case. One then says that the [[Hasse principle|Hasse principle]] applies to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100148.png" />. This terminology is explained by the fact that for an orthogonal group the injectivity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100149.png" /> is equivalent to the classical theorem of Minkowski–Hasse on quadratic forms, and in the case of a projective group it is equivalent to the Brauer–Hasse–Noether theorem on the splitting of simple algebras. According to a conjecture of Serre one always has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100150.png" /> for a simply-connected or adjoint semi-simple group. This conjecture was proved for most simply-connected semi-simple groups over global number fields (except for groups with simple components of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100151.png" />) , and also for arbitrary simply-connected algebraic groups over global function fields. | |
| − | |||
| − | which is denoted by < | ||
| − | |||
| − | |||
| − | of Abelian varieties, is called the Tate–Shafarevich group. The group | ||
| − | |||
| − | |||
| − | </ | ||
| − | extent to which the Galois cohomology groups over a global field are | ||
| − | described by Galois cohomology groups over localizations. The | ||
| − | principal result on < | ||
| − | |||
| − | |||
| − | algebraic groups is due to A. Borel, who proved that | ||
| − | |||
| − | |||
| − | </ | ||
| − | exists a conjecture according to which < | ||
| − | |||
| − | |||
| − | finite in the case of Abelian varieties as well. The situation in | ||
| − | which < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | a special case. One then says that the [[Hasse principle|Hasse | ||
| − | principle]] applies to < | ||
| − | |||
| − | |||
| − | is explained by the fact that for an orthogonal group the injectivity | ||
| − | of < | ||
| − | |||
| − | |||
| − | the classical theorem of Minkowski–Hasse on quadratic forms, and in | ||
| − | the case of a projective group it is equivalent to the | ||
| − | Brauer–Hasse–Noether theorem on the splitting of simple | ||
| − | algebras. According to a conjecture of Serre one always has | ||
| − | < | ||
| − | |||
| − | |||
| − | simply-connected or adjoint semi-simple group. This conjecture was | ||
| − | proved for most simply-connected semi-simple groups over global number | ||
| − | fields (except for groups with simple components of type | ||
| − | |||
| − | |||
| − | </ | ||
| − | arbitrary simply-connected algebraic groups over global function | ||
| − | fields. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J.-P. Serre, | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.W.S. Cassels (ed.) A. Fröhlich (ed.) , ''Algebraic number theory'' , Acad. Press (1986)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Koch, "Galoissche Theorie der <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100152.png" />-Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E. Artin, J. Tate, "Class field theory" , Benjamin (1967)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> J.-P. Serre, "Local fields" , Springer (1979) (Translated from French)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> A. Borel, J.-P. Serre, "Théorèmes de finitude en cohomologie Galoisienne" ''Comment Math. Helv.'' , '''39''' (1964) pp. 111–164</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> "Théorie des toposes et cohomologie étale des schémas" A. Grothendieck (ed.) J.-L. Verdier (ed.) E. Artin (ed.) , ''Sem. Geom. Alg. 4'' , '''1–3''' , Springer (1972)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> F. Bruhat, J. Tits, "Groupes réductifs sur un corps local I. Données radicielles valuées" ''Publ. Math. IHES'' : 41 (1972) pp. 5–252</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> A. Borel, "Some finiteness properties of adèle groups over number fields" ''Publ. Math. IHES'' : 16 (1963) pp. 5–30</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> R. Steinberg, "Regular elements of semisimple algebraic groups" ''Publ. Math. IHES'' : 25 (1965) pp. 49–80</TD></TR><TR><TD valign="top">[12a]</TD> <TD valign="top"> M. Kneser, "Galois-Kohomologie halbeinfacher algebraischer Gruppen über <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100153.png" />-adische Körpern I" ''Math. Z.'' , '''88''' (1965) pp. 40–47</TD></TR><TR><TD valign="top">[12b]</TD> <TD valign="top"> M. Kneser, "Galois-Kohomologie halbeinfacher algebraischer Gruppen über <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100154.png" />-adische Körpern II" ''Math. Z.'' , '''89''' (1965) pp. 250–272</TD></TR><TR><TD valign="top">[13a]</TD> <TD valign="top"> G. Harder, "Ueber die Galoiskohomologie halbeinfacher Matrizengruppen I" ''Math. Z.'' , '''90''' (1965) pp. 404–428</TD></TR><TR><TD valign="top">[13b]</TD> <TD valign="top"> G. Harder, "Ueber die Galoiskohomologie halbeinfacher Matrizengruppen II" ''Math. Z.'' , '''92''' (1966) pp. 396–415</TD></TR></table> |
| − | "Cohomologie Galoisienne" , Springer | ||
| − | (1964)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> | ||
| − | J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann | ||
| − | (1959)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> | ||
| − | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , ''Algebraic number theory'' | ||
| − | , Acad. Press | ||
| − | (1986)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> | ||
| − | H. Koch, "Galoissche Theorie der < | ||
| − | |||
| − | |||
| − | Deutsch. Verlag Wissenschaft. | ||
| − | (1970)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> | ||
| − | E. Artin, J. Tate, "Class field theory" , Benjamin | ||
| − | (1967)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> | ||
| − | J.-P. Serre, "Local fields" , Springer (1979) (Translated from | ||
| − | French)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> | ||
| − | A. Borel, J.-P. Serre, "Théorèmes de finitude en cohomologie | ||
| − | Galoisienne" ''Comment Math. Helv.'' , '''39''' (1964) | ||
| − | pp. 111–164</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> | ||
| − | "Théorie des toposes et cohomologie étale des schémas" A. Grothendieck | ||
| − | (ed.) J.-L. Verdier (ed.) E. Artin (ed.) , ''Sem. Geom. Alg. 4'' , | ||
| − | '''1–3''' , Springer | ||
| − | (1972)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> | ||
| − | F. Bruhat, J. Tits, "Groupes réductifs sur un corps local I. Données | ||
| − | radicielles valuées" ''Publ. Math. IHES'' : 41 (1972) | ||
| − | pp. 5–252</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> | ||
| − | A. Borel, "Some finiteness properties of adèle groups over number | ||
| − | fields" ''Publ. Math. IHES'' : 16 (1963) | ||
| − | pp. 5–30</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> | ||
| − | R. Steinberg, "Regular elements of semisimple algebraic groups" | ||
| − | ''Publ. Math. IHES'' : 25 (1965) | ||
| − | pp. 49–80</TD></TR><TR><TD valign="top">[12a]</TD> <TD valign="top"> | ||
| − | M. Kneser, "Galois-Kohomologie halbeinfacher algebraischer Gruppen | ||
| − | über < | ||
| − | |||
| − | |||
| − | I" ''Math. Z.'' , '''88''' (1965) | ||
| − | pp. 40–47</TD></TR><TR><TD valign="top">[12b]</TD> <TD valign="top"> | ||
| − | M. Kneser, "Galois-Kohomologie halbeinfacher algebraischer Gruppen | ||
| − | über < | ||
| − | |||
| − | |||
| − | II" ''Math. Z.'' , '''89''' (1965) | ||
| − | pp. 250–272</TD></TR><TR><TD valign="top">[13a]</TD> <TD valign="top"> | ||
| − | G. Harder, "Ueber die Galoiskohomologie halbeinfacher Matrizengruppen | ||
| − | I" ''Math. Z.'' , '''90''' (1965) | ||
| − | pp. 404–428</TD></TR><TR><TD valign="top">[13b]</TD> <TD valign="top"> | ||
| − | G. Harder, "Ueber die Galoiskohomologie halbeinfacher Matrizengruppen | ||
| − | II" ''Math. Z.'' , '''92''' (1966) pp. 396–415</TD></TR></table> | ||
| − | ====Comments==== Let < | + | ====Comments==== |
| − | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100155.png" /> be a finite (or pro-finite) group, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100156.png" /> a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100157.png" />-group, i.e. a group together with an action of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100158.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100159.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100160.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100161.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100162.png" /> be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100163.png" />-set, i.e. there is an action of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100164.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100165.png" />. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100166.png" /> acts <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100168.png" />-equivariantly on the right on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100169.png" /> if there is given a right action <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100170.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100171.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100172.png" />. Such a right <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100173.png" />-set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100174.png" /> is a principal homogeneous space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100175.png" /> if the action makes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100176.png" /> an affine space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100177.png" /> (an affine version of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100178.png" />), i.e. if for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100179.png" /> there is a unique <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100180.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100181.png" />. (This is precisely the situation of a vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100182.png" /> and its corresponding affine space.) There is a natural bijective correspondence between isomorphism classes of principal homogeneous spaces over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100183.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100184.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100185.png" /> is a principal homogeneous space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100186.png" />, choose <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100187.png" /> and for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100188.png" /> define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100189.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100190.png" />. This defines the corresponding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100191.png" />-cocycle. | |
| − | |||
| − | pro-finite) group, < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | group together with an action of < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | < | ||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | </ | ||
| − | is an action of < | ||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | the right on < | ||
| − | |||
| − | |||
| − | a right action < | ||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | < | ||
| − | g | ||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | </ | ||
| − | homogeneous space over < | ||
| − | |||
| − | |||
| − | makes < | ||
| − | |||
| − | |||
| − | over < | ||
| − | |||
| − | |||
| − | version of < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | </ | ||
| − | < | ||
| − | |||
| − | |||
| − | precisely the situation of a vector space < | ||
| − | |||
| − | |||
| − | its corresponding affine space.) There is a natural bijective | ||
| − | correspondence between isomorphism classes of principal homogeneous | ||
| − | spaces over < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | </ | ||
| − | homogeneous space over < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | < | ||
| − | g | ||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | < | ||
| − | g | ||
| − | |||
| − | corresponding < | ||
| − | |||
| − | |||
| − | Let < | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100192.png" /> be a cyclic Galois extension of (commutative) fields of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100193.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100194.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100195.png" /> be an element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100196.png" />. Let the algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100197.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100198.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100199.png" /> be constructed as follows: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100200.png" /> for some symbol <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100201.png" />, with the multiplication rules <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100202.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100203.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100204.png" />. This defines an associative non-commutative algebra over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100205.png" />. Such an algebra is called a cyclic algebra. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100206.png" /> it is a central simple algebra with centre <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100207.png" />. The Brauer–Hasse–Noether theorem, [[#References|[a8]]], now says that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100208.png" /> is a finite-dimensional division algebra over its centre <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100209.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100210.png" /> is an algebraic number field, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100211.png" /> is a cyclic algebra. The same conclusion holds if instead <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100212.png" /> is a finite extension of one of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100213.png" />-adic fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100214.png" />, [[#References|[a7]]]. |
| − | |||
| − | |||
| − | Galois extension of (commutative) fields of degree | ||
| − | |||
| − | |||
| − | </ | ||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | </ | ||
| − | follows: < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | multiplication rules < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | associative non-commutative algebra over < | ||
| − | |||
| − | |||
| − | an algebra is called a cyclic algebra. If < | ||
| − | |||
| − | |||
| − | a central simple algebra with centre < | ||
| − | |||
| − | |||
| − | Brauer–Hasse–Noether theorem, [[#References|[a8]]], now says that if | ||
| − | |||
| − | |||
| − | </ | ||
| − | finite-dimensional division algebra over its centre | ||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | </ | ||
| − | number field, then < | ||
| − | |||
| − | |||
| − | algebra. The same conclusion holds if instead < | ||
| − | |||
| − | |||
| − | finite extension of one of the < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | [[#References|[a7]]]. | ||
| − | For the Minkowski–Hasse theorem on quadratic forms see [[Quadratic | + | For the Minkowski–Hasse theorem on quadratic forms see [[Quadratic form|Quadratic form]]. |
| − | form|Quadratic form]]. | ||
| − | Cohomology of Galois groups is also used in the birational | + | Cohomology of Galois groups is also used in the birational classification of rational varieties over not algebraically closed fields (cf. also [[Rational variety|Rational variety]]). An important birational invariant is the cohomology group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100215.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100216.png" /> is the [[Picard group|Picard group]] of the variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100217.png" /> which is defined over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100218.png" />. As in the case of algebraic groups, Galois cohomology provides important tools in the study of arithmetical properties of rational varieties. The use of Galois cohomology for the study of birational and arithmetical characteristics of rational varieties was initiated by Yu.I. Manin in the 1960s (see [[#References|[a1]]]) and was continued by J.-L. Colliot-Thélène and J.J. Sansuc (see [[#References|[a2]]]), V.E. Voskresenskii ([[#References|[a3]]]), etc. |
| − | classification of rational varieties over not algebraically closed | ||
| − | fields (cf. also [[Rational variety|Rational variety]]). An important | ||
| − | birational invariant is the cohomology group < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | group|Picard group]] of the variety < | ||
| − | |||
| − | |||
| − | over a field < | ||
| − | |||
| − | |||
| − | of algebraic groups, Galois cohomology provides important tools in the | ||
| − | study of arithmetical properties of rational varieties. The use of | ||
| − | Galois cohomology for the study of birational and arithmetical | ||
| − | characteristics of rational varieties was initiated by Yu.I. Manin in | ||
| − | the 1960s (see [[#References|[a1]]]) and was continued by | ||
| − | J.-L. Colliot-Thélène and J.J. Sansuc (see [[#References|[a2]]]), | ||
| − | V.E. Voskresenskii ([[#References|[a3]]]), etc. | ||
| − | It was proved recently (1988) by V.I. Chernusov [[#References|[a4]]] | + | It was proved recently (1988) by V.I. Chernusov [[#References|[a4]]] that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100219.png" /> for a simple group of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100220.png" /> over a number field. It follows that the [[Hasse principle|Hasse principle]] holds for simply-connected semi-simple algebraic groups over number fields. |
| − | that < | ||
| − | |||
| − | |||
| − | group of type < | ||
| − | |||
| − | |||
| − | field. It follows that the [[Hasse principle|Hasse principle]] holds | ||
| − | for simply-connected semi-simple algebraic groups over number fields. | ||
| − | For a proof of the general case of the Kneser–Bruhat–Tits theorem see, | + | For a proof of the general case of the Kneser–Bruhat–Tits theorem see, e.g., [[#References|[a5]]]. |
| − | e.g., [[#References|[a5]]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> Yu.I. Manin, | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> Yu.I. Manin, "Cubic forms. Algebra, geometry, arithmetic" , North-Holland (1974) (Translated from Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.-L. Colliot-Thélène, J.J. Sansuc, "La descente sur les variétés rationnelles II" ''Duke Math. J.'' , '''54''' (1987) pp. 375–492</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> V.E. Voskresenskii, "Algebraic tori" , Moscow (1977) (In Russian)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> V.I. Chernusov, "On the Hasse principle for groups of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043100/g043100221.png" />" (To appear) (In Russian)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> F. Bruhat, J. Tits, "Groupes réductifs sur un corps local III. Complements et applications à la cohomologie Galoisiènne" ''J. Fac. Sci. Univ. Tokyo'' , '''34''' (1987) pp. 671–698</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> G. Harder, "Chevalley groups over function fields and automorphic forms" ''Ann. of Math.'' , '''100''' (1974) pp. 249–306</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> A.A. Albert, "Structure of algebras" , Amer. Math. Soc. (1939) pp. 143</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> R. Brauer, H. Hasse, E. Noether, "Beweis eines Haupsatzes in der Theorie der Algebren" ''J. Reine Angew. Math.'' , '''107''' (1931) pp. 399–404</TD></TR></table> |
| − | "Cubic forms. Algebra, geometry, arithmetic" , North-Holland (1974) | ||
| − | (Translated from | ||
| − | Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> | ||
| − | J.-L. Colliot-Thélène, J.J. Sansuc, "La descente sur les variétés | ||
| − | rationnelles II" ''Duke Math. J.'' , '''54''' (1987) | ||
| − | pp. 375–492</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> | ||
| − | V.E. Voskresenskii, "Algebraic tori" , Moscow (1977) (In | ||
| − | Russian)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> | ||
| − | V.I. Chernusov, "On the Hasse principle for groups of type | ||
| − | |||
| − | |||
| − | </ | ||
| − | Russian)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> | ||
| − | F. Bruhat, J. Tits, "Groupes réductifs sur un corps local | ||
| − | III. Complements et applications à la cohomologie Galoisiènne" | ||
| − | ''J. Fac. Sci. Univ. Tokyo'' , '''34''' (1987) | ||
| − | pp. 671–698</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> | ||
| − | G. Harder, "Chevalley groups over function fields and automorphic | ||
| − | forms" ''Ann. of Math.'' , '''100''' (1974) | ||
| − | pp. 249–306</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> | ||
| − | A.A. Albert, "Structure of algebras" , Amer. Math. Soc. (1939) | ||
| − | pp. 143</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> | ||
| − | R. Brauer, H. Hasse, E. Noether, "Beweis eines Haupsatzes in der | ||
| − | Theorie der Algebren" ''J. Reine Angew. Math.'' , '''107''' (1931) | ||
| − | pp. 399–404</TD></TR></table> | ||
Revision as of 23:04, 20 June 2011
Cohomology of a Galois group. Let 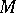 be an Abelian group, let
be an Abelian group, let 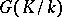 be the Galois group of an extension
be the Galois group of an extension 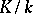 and suppose
and suppose 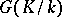 acts on
acts on 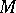 ; the Galois cohomology groups will then be the cohomology groups
; the Galois cohomology groups will then be the cohomology groups
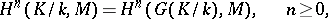 |
defined by the complex 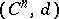 , where
, where 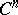 consists of all mappings
consists of all mappings 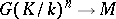 and
and 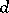 is the coboundary operator (cf. Cohomology of groups). If
is the coboundary operator (cf. Cohomology of groups). If 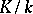 is an extension of infinite degree, an additional requirement is that the Galois topological group acts continuously on the discrete group
is an extension of infinite degree, an additional requirement is that the Galois topological group acts continuously on the discrete group 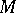 , and continuous mappings are taken for the cochains in
, and continuous mappings are taken for the cochains in 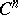 .
.
Usually, only zero-dimensional 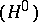 and one-dimensional
and one-dimensional 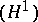 cohomology are defined for a non-Abelian group
cohomology are defined for a non-Abelian group 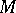 . Namely,
. Namely, 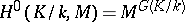 is the set of fixed points under the group
is the set of fixed points under the group 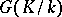 in
in 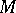 , while
, while 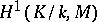 is the quotient set of the set of one-dimensional cocycles, i.e. continuous mappings
is the quotient set of the set of one-dimensional cocycles, i.e. continuous mappings 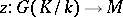 that satisfy the relation
that satisfy the relation
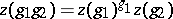 |
for all 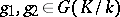 , by the equivalence relation
, by the equivalence relation  , where
, where 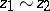 if and only if
if and only if 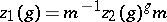 for some
for some 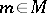 and all
and all 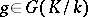 . In the non-Abelian case
. In the non-Abelian case 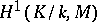 is a set with a distinguished point corresponding to the trivial cocycle
is a set with a distinguished point corresponding to the trivial cocycle 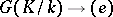 , where
, where  is the unit of
is the unit of 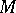 , and usually has no group structure. Nevertheless, a standard cohomology formalism can be developed for such cohomology as well (cf. Non-Abelian cohomology).
, and usually has no group structure. Nevertheless, a standard cohomology formalism can be developed for such cohomology as well (cf. Non-Abelian cohomology).
If 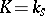 is the separable closure of a field
is the separable closure of a field  , it is customary to denote the group
, it is customary to denote the group 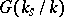 by
by 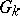 , and to write
, and to write 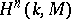 for
for 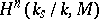 .
.
Galois cohomology groups were implicitly present in the work of D. Hilbert, E. Artin, R. Brauer, H. Hasse, and C. Chevalley on class field theory, finite-dimensional simple algebras and quadratic forms. The development of the ideas and methods of homological algebra resulted in the introduction of Galois cohomology groups of finite extensions with values in an Abelian group by E. Artin, A. Weil, G. Hochschild, and J. Tate in the 1950s, in connection with class field theory. The general theory of Abelian Galois cohomology groups was then developed by Tate and J.-P. Serre [1], [3], [6].
Tate used Galois cohomology to introduce the concept of the cohomological dimension of the Galois group 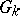 of a field
of a field 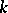 (denoted by
(denoted by 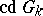 ). It is defined in terms of the cohomological
). It is defined in terms of the cohomological 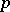 -dimension
-dimension 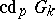 , which is the smallest integer
, which is the smallest integer  such that for any torsion
such that for any torsion 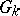 -module
-module 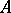 and any integer
and any integer 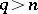 the
the 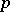 -primary component of the group
-primary component of the group 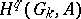 is zero. The cohomological dimension
is zero. The cohomological dimension  is
is
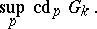 |
For any algebraically closed field 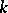 one has
one has 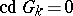 ; for all fields
; for all fields 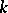 such that the Brauer group
such that the Brauer group 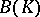 of an arbitrary extension
of an arbitrary extension 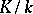 is trivial,
is trivial, 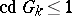 ; for the
; for the 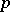 -adic field, the field of algebraic functions of one variable over a finite field of constants and for a totally-complex number field,
-adic field, the field of algebraic functions of one variable over a finite field of constants and for a totally-complex number field, 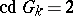 [1]. Fields
[1]. Fields 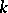 whose Galois group has cohomological dimension
whose Galois group has cohomological dimension 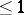 and whose Brauer group
and whose Brauer group 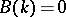 are called fields of dimension
are called fields of dimension 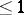 ; this is denoted by
; this is denoted by 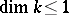 . Such fields include all finite fields, maximal unramified extensions of
. Such fields include all finite fields, maximal unramified extensions of 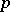 -adic fields, and the field of rational functions in one variable over an algebraically closed field of constants. If a Galois group
-adic fields, and the field of rational functions in one variable over an algebraically closed field of constants. If a Galois group 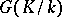 is a pro-
is a pro-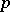 -group, i.e. is the projective limit of finite
-group, i.e. is the projective limit of finite 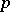 -groups, the dimension of
-groups, the dimension of 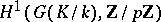 over
over 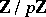 is equal to the minimal number of topological generators of
is equal to the minimal number of topological generators of 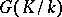 , while the dimension of
, while the dimension of 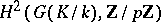 is the number of defining relations between these generators. If
is the number of defining relations between these generators. If 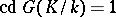 , then
, then 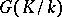 is a free pro-
is a free pro-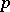 -group.
-group.
Non-Abelian Galois cohomology appeared in the late 1950s, but systematic research began only in the 1960s, mainly in response to the need for the classification of algebraic groups over not algebraically closed fields. One of the principal problems which stimulated the development of non-Abelian Galois cohomology is the task of classifying principal homogeneous spaces of group schemes. Galois cohomology groups proved to be specially effective in the problem of classifying types of algebraic varieties.
These problems led to the problem of computing the Galois cohomology groups of algebraic groups. The general theorems on the structure of algebraic groups essentially reduce the study of Galois cohomology groups to a separate consideration of the Galois cohomology groups of finite groups, unipotent groups, tori, semi-simple groups, and Abelian varieties.
The Galois cohomology groups of a connected unipotent group 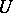 are trivial if
are trivial if 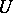 is defined over a perfect field
is defined over a perfect field 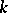 , i.e.
, i.e.  for an arbitrary unipotent group
for an arbitrary unipotent group 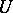 , and
, and 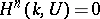 for all
for all 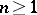 if
if 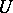 is an Abelian group. In particular, for the additive group
is an Abelian group. In particular, for the additive group 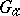 of an arbitrary field one always has
of an arbitrary field one always has 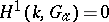 . For an imperfect field
. For an imperfect field 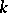 , in general
, in general 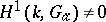 .
.
One of the first significant facts about Galois cohomology groups was Hilbert's "Theorem 90" , one formulation of which states that 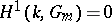 (where
(where 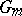 is the multiplicative group). Moreover, for any
is the multiplicative group). Moreover, for any 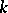 -split algebraic torus
-split algebraic torus 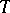 one has
one has 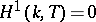 . The computation of
. The computation of 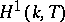 for an arbitrary
for an arbitrary 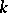 -defined torus
-defined torus  can be reduced, in the general case, to the computation of
can be reduced, in the general case, to the computation of 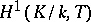 where
where 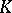 is a Galois splitting field of
is a Galois splitting field of 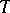 ; so far (1989) this has only been accomplished for special fields. The case when
; so far (1989) this has only been accomplished for special fields. The case when  is an algebraic number field is especially important in practical applications. Duality theorems, with various applications, have been developed for this case.
is an algebraic number field is especially important in practical applications. Duality theorems, with various applications, have been developed for this case.
Let 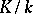 be a Galois extension of finite degree, let
be a Galois extension of finite degree, let 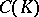 be the group of adèles (cf. Adèle) of a multiplicative
be the group of adèles (cf. Adèle) of a multiplicative 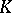 -group
-group 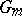 , and let
, and let 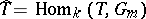 be the group of characters of a torus. The duality theorem states that the cup-product
be the group of characters of a torus. The duality theorem states that the cup-product
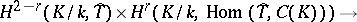 |
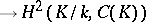 |
defines non-degenerate pairing for 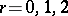 . This theorem was used to find the formula for expressing the Tamagawa numbers (cf. Tamagawa number) of the torus
. This theorem was used to find the formula for expressing the Tamagawa numbers (cf. Tamagawa number) of the torus 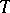 by invariants connected with its Galois cohomology groups. Other important duality theorems for Galois cohomology groups also exist [1].
by invariants connected with its Galois cohomology groups. Other important duality theorems for Galois cohomology groups also exist [1].
It has been proved [11] that the groups 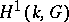 over fields
over fields 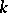 of dimension
of dimension 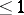 are trivial. A natural class of fields has been distinguished with only a finite number of extensions of a given degree (the so-called type
are trivial. A natural class of fields has been distinguished with only a finite number of extensions of a given degree (the so-called type  fields); these include, for example, the
fields); these include, for example, the 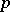 -adic number fields. It was proved [1] that for any algebraic group
-adic number fields. It was proved [1] that for any algebraic group 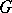 over a field
over a field 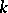 of type
of type 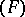 the cohomology group
the cohomology group 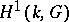 is a finite set.
is a finite set.
The theory of Galois cohomology of semi-simple algebraic groups has far-reaching arithmetical and analytical applications. The Kneser–Bruhat–Tits theorem states that 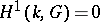 for simply-connected semi-simple algebraic groups
for simply-connected semi-simple algebraic groups 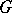 over local fields
over local fields 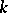 whose residue field has cohomological dimension
whose residue field has cohomological dimension  . This theorem was first proved for
. This theorem was first proved for  -adic number fields , after which a proof was obtained for the general case. It was proved
-adic number fields , after which a proof was obtained for the general case. It was proved
that 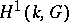 is trivial for a field of algebraic functions in one variable over a finite field of constants. In all these cases the cohomological dimension
is trivial for a field of algebraic functions in one variable over a finite field of constants. In all these cases the cohomological dimension 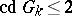 , which confirms the general conjecture of Serre to the effect that
, which confirms the general conjecture of Serre to the effect that  is trivial for simply-connected semi-simple
is trivial for simply-connected semi-simple 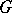 over fields
over fields  with
with 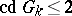 .
.
Let 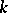 be a global field, let
be a global field, let 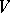 be the set of all non-equivalent valuations of
be the set of all non-equivalent valuations of 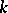 , let
, let 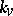 be the completion of
be the completion of 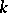 . The imbeddings
. The imbeddings 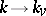 induce a natural mapping
induce a natural mapping
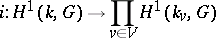 |
for an arbitrary algebraic group 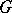 defined over
defined over 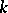 , the kernel of which is denoted by
, the kernel of which is denoted by 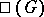 and, in the case of Abelian varieties, is called the Tate–Shafarevich group. The group
and, in the case of Abelian varieties, is called the Tate–Shafarevich group. The group 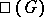 measures the extent to which the Galois cohomology groups over a global field are described by Galois cohomology groups over localizations. The principal result on
measures the extent to which the Galois cohomology groups over a global field are described by Galois cohomology groups over localizations. The principal result on 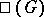 for linear algebraic groups is due to A. Borel, who proved that
for linear algebraic groups is due to A. Borel, who proved that 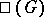 is finite. There exists a conjecture according to which
is finite. There exists a conjecture according to which 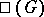 is finite in the case of Abelian varieties as well. The situation in which
is finite in the case of Abelian varieties as well. The situation in which 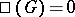 , i.e. the mapping
, i.e. the mapping 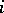 is injective, is a special case. One then says that the Hasse principle applies to
is injective, is a special case. One then says that the Hasse principle applies to 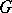 . This terminology is explained by the fact that for an orthogonal group the injectivity of
. This terminology is explained by the fact that for an orthogonal group the injectivity of 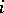 is equivalent to the classical theorem of Minkowski–Hasse on quadratic forms, and in the case of a projective group it is equivalent to the Brauer–Hasse–Noether theorem on the splitting of simple algebras. According to a conjecture of Serre one always has
is equivalent to the classical theorem of Minkowski–Hasse on quadratic forms, and in the case of a projective group it is equivalent to the Brauer–Hasse–Noether theorem on the splitting of simple algebras. According to a conjecture of Serre one always has 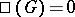 for a simply-connected or adjoint semi-simple group. This conjecture was proved for most simply-connected semi-simple groups over global number fields (except for groups with simple components of type
for a simply-connected or adjoint semi-simple group. This conjecture was proved for most simply-connected semi-simple groups over global number fields (except for groups with simple components of type 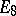 ) , and also for arbitrary simply-connected algebraic groups over global function fields.
) , and also for arbitrary simply-connected algebraic groups over global function fields.
References
| [1] | J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964) |
| [2] | J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959) |
| [3] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
| [4] | H. Koch, "Galoissche Theorie der 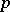 -Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970) -Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970) |
| [5] | E. Artin, J. Tate, "Class field theory" , Benjamin (1967) |
| [6] | J.-P. Serre, "Local fields" , Springer (1979) (Translated from French) |
| [7] | A. Borel, J.-P. Serre, "Théorèmes de finitude en cohomologie Galoisienne" Comment Math. Helv. , 39 (1964) pp. 111–164 |
| [8] | "Théorie des toposes et cohomologie étale des schémas" A. Grothendieck (ed.) J.-L. Verdier (ed.) E. Artin (ed.) , Sem. Geom. Alg. 4 , 1–3 , Springer (1972) |
| [9] | F. Bruhat, J. Tits, "Groupes réductifs sur un corps local I. Données radicielles valuées" Publ. Math. IHES : 41 (1972) pp. 5–252 |
| [10] | A. Borel, "Some finiteness properties of adèle groups over number fields" Publ. Math. IHES : 16 (1963) pp. 5–30 |
| [11] | R. Steinberg, "Regular elements of semisimple algebraic groups" Publ. Math. IHES : 25 (1965) pp. 49–80 |
| [12a] | M. Kneser, "Galois-Kohomologie halbeinfacher algebraischer Gruppen über 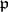 -adische Körpern I" Math. Z. , 88 (1965) pp. 40–47 -adische Körpern I" Math. Z. , 88 (1965) pp. 40–47 |
| [12b] | M. Kneser, "Galois-Kohomologie halbeinfacher algebraischer Gruppen über 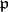 -adische Körpern II" Math. Z. , 89 (1965) pp. 250–272 -adische Körpern II" Math. Z. , 89 (1965) pp. 250–272 |
| [13a] | G. Harder, "Ueber die Galoiskohomologie halbeinfacher Matrizengruppen I" Math. Z. , 90 (1965) pp. 404–428 |
| [13b] | G. Harder, "Ueber die Galoiskohomologie halbeinfacher Matrizengruppen II" Math. Z. , 92 (1966) pp. 396–415 |
Comments
Let 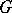 be a finite (or pro-finite) group,
be a finite (or pro-finite) group, 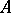 a
a 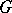 -group, i.e. a group together with an action of
-group, i.e. a group together with an action of 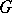 on
on 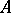 ,
, 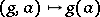 , such that
, such that 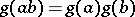 , and let
, and let 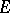 be a
be a 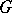 -set, i.e. there is an action of
-set, i.e. there is an action of 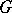 on
on 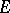 .
. 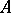 acts
acts 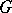 -equivariantly on the right on
-equivariantly on the right on 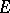 if there is given a right action
if there is given a right action 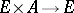 ,
,  , such that
, such that  . Such a right
. Such a right 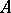 -set
-set 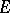 is a principal homogeneous space over
is a principal homogeneous space over 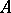 if the action makes
if the action makes  an affine space over
an affine space over 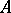 (an affine version of
(an affine version of 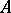 ), i.e. if for all
), i.e. if for all 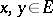 there is a unique
there is a unique 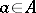 such that
such that 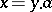 . (This is precisely the situation of a vector space
. (This is precisely the situation of a vector space 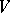 and its corresponding affine space.) There is a natural bijective correspondence between isomorphism classes of principal homogeneous spaces over
and its corresponding affine space.) There is a natural bijective correspondence between isomorphism classes of principal homogeneous spaces over 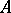 and
and 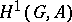 . If
. If 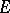 is a principal homogeneous space over
is a principal homogeneous space over 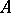 , choose
, choose 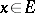 and for
and for 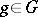 define
define 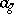 by
by 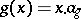 . This defines the corresponding
. This defines the corresponding 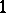 -cocycle.
-cocycle.
Let 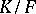 be a cyclic Galois extension of (commutative) fields of degree
be a cyclic Galois extension of (commutative) fields of degree 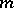 . Let
. Let 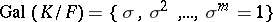 . Let
. Let 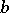 be an element of
be an element of 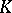 . Let the algebra
. Let the algebra 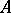 of dimension
of dimension 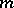 over
over 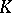 be constructed as follows:
be constructed as follows: 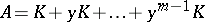 for some symbol
for some symbol 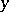 , with the multiplication rules
, with the multiplication rules 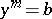 ,
, 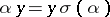 for all
for all  . This defines an associative non-commutative algebra over
. This defines an associative non-commutative algebra over 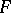 . Such an algebra is called a cyclic algebra. If
. Such an algebra is called a cyclic algebra. If 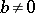 it is a central simple algebra with centre
it is a central simple algebra with centre 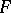 . The Brauer–Hasse–Noether theorem, [a8], now says that if
. The Brauer–Hasse–Noether theorem, [a8], now says that if 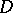 is a finite-dimensional division algebra over its centre
is a finite-dimensional division algebra over its centre  and
and 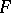 is an algebraic number field, then
is an algebraic number field, then 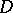 is a cyclic algebra. The same conclusion holds if instead
is a cyclic algebra. The same conclusion holds if instead 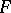 is a finite extension of one of the
is a finite extension of one of the 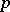 -adic fields
-adic fields 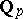 , [a7].
, [a7].
For the Minkowski–Hasse theorem on quadratic forms see Quadratic form.
Cohomology of Galois groups is also used in the birational classification of rational varieties over not algebraically closed fields (cf. also Rational variety). An important birational invariant is the cohomology group 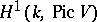 , where
, where 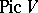 is the Picard group of the variety
is the Picard group of the variety 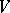 which is defined over a field
which is defined over a field 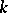 . As in the case of algebraic groups, Galois cohomology provides important tools in the study of arithmetical properties of rational varieties. The use of Galois cohomology for the study of birational and arithmetical characteristics of rational varieties was initiated by Yu.I. Manin in the 1960s (see [a1]) and was continued by J.-L. Colliot-Thélène and J.J. Sansuc (see [a2]), V.E. Voskresenskii ([a3]), etc.
. As in the case of algebraic groups, Galois cohomology provides important tools in the study of arithmetical properties of rational varieties. The use of Galois cohomology for the study of birational and arithmetical characteristics of rational varieties was initiated by Yu.I. Manin in the 1960s (see [a1]) and was continued by J.-L. Colliot-Thélène and J.J. Sansuc (see [a2]), V.E. Voskresenskii ([a3]), etc.
It was proved recently (1988) by V.I. Chernusov [a4] that  for a simple group of type
for a simple group of type  over a number field. It follows that the Hasse principle holds for simply-connected semi-simple algebraic groups over number fields.
over a number field. It follows that the Hasse principle holds for simply-connected semi-simple algebraic groups over number fields.
For a proof of the general case of the Kneser–Bruhat–Tits theorem see, e.g., [a5].
References
| [a1] | Yu.I. Manin, "Cubic forms. Algebra, geometry, arithmetic" , North-Holland (1974) (Translated from Russian) |
| [a2] | J.-L. Colliot-Thélène, J.J. Sansuc, "La descente sur les variétés rationnelles II" Duke Math. J. , 54 (1987) pp. 375–492 |
| [a3] | V.E. Voskresenskii, "Algebraic tori" , Moscow (1977) (In Russian) |
| [a4] | V.I. Chernusov, "On the Hasse principle for groups of type  " (To appear) (In Russian) " (To appear) (In Russian) |
| [a5] | F. Bruhat, J. Tits, "Groupes réductifs sur un corps local III. Complements et applications à la cohomologie Galoisiènne" J. Fac. Sci. Univ. Tokyo , 34 (1987) pp. 671–698 |
| [a6] | G. Harder, "Chevalley groups over function fields and automorphic forms" Ann. of Math. , 100 (1974) pp. 249–306 |
| [a7] | A.A. Albert, "Structure of algebras" , Amer. Math. Soc. (1939) pp. 143 |
| [a8] | R. Brauer, H. Hasse, E. Noether, "Beweis eines Haupsatzes in der Theorie der Algebren" J. Reine Angew. Math. , 107 (1931) pp. 399–404 |
Galois cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galois_cohomology&oldid=19461