Difference between revisions of "Functor"
m (→Comments: link) |
m (link) |
||
| Line 18: | Line 18: | ||
1) The identity mapping of a category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214033.png" /> onto itself is a covariant functor, called the identity functor of the category and denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214034.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214035.png" />. | 1) The identity mapping of a category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214033.png" /> onto itself is a covariant functor, called the identity functor of the category and denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214034.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214035.png" />. | ||
| − | 2) Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214036.png" /> be an arbitrary locally small category, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214037.png" /> be the category of sets, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214038.png" /> be a fixed object of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214039.png" />. If one associates to each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214040.png" /> the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214041.png" /> and to each morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214042.png" /> the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214043.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214044.png" /> for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214045.png" />, one obtains a functor from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214046.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214047.png" />. This functor is called the covariant representable functor from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214048.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214049.png" /> with representing object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214050.png" />. Similarly, if one associates to an object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214051.png" /> the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214052.png" /> and to a morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214053.png" /> the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214054.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214055.png" />, one obtains the contravariant representable functor from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214056.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214057.png" /> with representing object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214058.png" />. These functors are denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214059.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214060.png" />, respectively. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214061.png" /> is the category of vector spaces over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214062.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214063.png" /> takes a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214064.png" /> to its dual space of linear functionals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214065.png" />. In the category of topological Abelian groups, the functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214066.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214067.png" /> is the quotient group of the real numbers by the integers, associates to each group its group of characters. | + | 2) Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214036.png" /> be an arbitrary [[locally small category]], let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214037.png" /> be the category of sets, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214038.png" /> be a fixed object of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214039.png" />. If one associates to each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214040.png" /> the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214041.png" /> and to each morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214042.png" /> the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214043.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214044.png" /> for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214045.png" />, one obtains a functor from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214046.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214047.png" />. This functor is called the covariant representable functor from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214048.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214049.png" /> with representing object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214050.png" />. Similarly, if one associates to an object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214051.png" /> the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214052.png" /> and to a morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214053.png" /> the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214054.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214055.png" />, one obtains the contravariant representable functor from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214056.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214057.png" /> with representing object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214058.png" />. These functors are denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214059.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214060.png" />, respectively. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214061.png" /> is the category of vector spaces over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214062.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214063.png" /> takes a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214064.png" /> to its dual space of linear functionals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214065.png" />. In the category of topological Abelian groups, the functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214066.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214067.png" /> is the quotient group of the real numbers by the integers, associates to each group its group of characters. |
3) If one associates to each pair of objects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214068.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214069.png" /> of an arbitrary category the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214070.png" />, and to each pair of morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214071.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214072.png" /> the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214073.png" /> defined by the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214074.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214075.png" />, one obtains a two-place functor into the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214076.png" /> that is contravariant in the first argument and covariant in the second. | 3) If one associates to each pair of objects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214068.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214069.png" /> of an arbitrary category the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214070.png" />, and to each pair of morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214071.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214072.png" /> the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214073.png" /> defined by the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214074.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214075.png" />, one obtains a two-place functor into the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042140/f04214076.png" /> that is contravariant in the first argument and covariant in the second. | ||
Revision as of 16:12, 29 October 2016
A mapping from one category into another that is compatible with the category structure. More precisely, a covariant functor from a category  into a category
into a category  or, simply, a functor from
or, simply, a functor from  into
into  , is a pair of mappings
, is a pair of mappings  , usually denoted by the same letter, for example
, usually denoted by the same letter, for example  (
( ), subject to the conditions:
), subject to the conditions:
1)  for every
for every  ;
;
2) 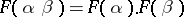 for all morphisms
for all morphisms 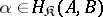 ,
,  .
.
A functor from the category  dual to
dual to  into the category
into the category  is called a contravariant functor from
is called a contravariant functor from  into
into  . Thus, for a contravariant functor
. Thus, for a contravariant functor 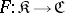 , condition 1) must be satisfied as before, and condition 2) is replaced by: 2*)
, condition 1) must be satisfied as before, and condition 2) is replaced by: 2*)  for all morphisms
for all morphisms  ,
,  .
.
An  -place functor from categories
-place functor from categories  into
into  that is covariant in the arguments
that is covariant in the arguments  and contravariant in the remaining arguments is a functor from the Cartesian product
and contravariant in the remaining arguments is a functor from the Cartesian product
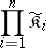 |
into  , where
, where  for
for  and
and  for the remaining
for the remaining 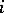 . Two-place functors that are covariant in both arguments are called bifunctors.
. Two-place functors that are covariant in both arguments are called bifunctors.
Examples of functors.
1) The identity mapping of a category  onto itself is a covariant functor, called the identity functor of the category and denoted by
onto itself is a covariant functor, called the identity functor of the category and denoted by  or
or  .
.
2) Let  be an arbitrary locally small category, let
be an arbitrary locally small category, let  be the category of sets, and let
be the category of sets, and let  be a fixed object of
be a fixed object of  . If one associates to each
. If one associates to each  the set
the set  and to each morphism
and to each morphism  the mapping
the mapping 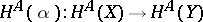 , where
, where 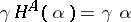 for each
for each  , one obtains a functor from
, one obtains a functor from  into
into 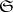 . This functor is called the covariant representable functor from
. This functor is called the covariant representable functor from  into
into 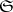 with representing object
with representing object  . Similarly, if one associates to an object
. Similarly, if one associates to an object  the set
the set  and to a morphism
and to a morphism  the mapping
the mapping 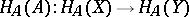 , where
, where  , one obtains the contravariant representable functor from
, one obtains the contravariant representable functor from  into
into  with representing object
with representing object  . These functors are denoted by
. These functors are denoted by 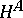 and
and  , respectively. If
, respectively. If  is the category of vector spaces over a field
is the category of vector spaces over a field  , then
, then 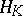 takes a space
takes a space  to its dual space of linear functionals
to its dual space of linear functionals  . In the category of topological Abelian groups, the functor
. In the category of topological Abelian groups, the functor 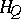 , where
, where  is the quotient group of the real numbers by the integers, associates to each group its group of characters.
is the quotient group of the real numbers by the integers, associates to each group its group of characters.
3) If one associates to each pair of objects  and
and  of an arbitrary category the set
of an arbitrary category the set  , and to each pair of morphisms
, and to each pair of morphisms  and
and 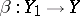 the mapping
the mapping  defined by the equation
defined by the equation  for any
for any  , one obtains a two-place functor into the category
, one obtains a two-place functor into the category  that is contravariant in the first argument and covariant in the second.
that is contravariant in the first argument and covariant in the second.
In any category with finite products, the product can be regarded as an  -place functor that is covariant in all arguments, for any natural number
-place functor that is covariant in all arguments, for any natural number  . As a rule, a construction that may be defined for any object of a category or for any sequence of objects of a fixed length, independently of the individual properties of the objects, is likely to be functorial. Examples of this are the construction of free algebras in some variety of universal algebras, which can be uniquely associated to each object of the category of sets; the construction of the fundamental group of a topological space, the construction of homology and cohomology groups of various dimensions; etc.
. As a rule, a construction that may be defined for any object of a category or for any sequence of objects of a fixed length, independently of the individual properties of the objects, is likely to be functorial. Examples of this are the construction of free algebras in some variety of universal algebras, which can be uniquely associated to each object of the category of sets; the construction of the fundamental group of a topological space, the construction of homology and cohomology groups of various dimensions; etc.
Any functor  defines a mapping of each set
defines a mapping of each set  into
into  which associates to a morphism
which associates to a morphism  the morphism
the morphism  . The functor
. The functor  is called faithful if these mappings are all injective, and full if they are all surjective. For every small category
is called faithful if these mappings are all injective, and full if they are all surjective. For every small category  , the assignment
, the assignment  can be extended to a full faithful functor
can be extended to a full faithful functor  from
from 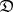 into the category
into the category 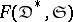 of diagrams (cf. Diagram) with scheme
of diagrams (cf. Diagram) with scheme  over the category of sets
over the category of sets  .
.
References
| [1] | I. Bucur, A. Deleanu, "Introduction to the theory of categories and functors" , Wiley (1968) |
| [2] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
| [3] | S. MacLane, "Categories for the working mathematician" , Springer (1971) |
| [4] | H. Schubert, "Categories" , 1–2 , Springer (1972) |
| [5] | M.Sh. Tsalenko, E.G. Shul'geifer, "Fundamentals of category theory" , Moscow (1974) (In Russian) |
Comments
A subfunctor of a given functor  is a functor
is a functor  together with a morphism of functors (functorial transformation)
together with a morphism of functors (functorial transformation)  such that for each
such that for each  ,
,  is a monomorphism in
is a monomorphism in  (and thus represents a subobject of
(and thus represents a subobject of  ). Dually, a quotient functor of
). Dually, a quotient functor of  is a functor
is a functor 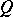 with a functorial transformation
with a functorial transformation  which yields an epimorphism
which yields an epimorphism 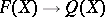 for each
for each 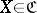 . It follows that then
. It follows that then 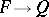 is an epimorphism in the category
is an epimorphism in the category  of functors from
of functors from  .
.
In some translations into English (including in some earlier articles in this Encyclopaedia) the terms "faithful functor" and "full functor" are (mis)translated as "univalent functor" and "complete functor" , respectively.
The full and faithful functor  mentioned at the end of the main article is often called the "Yoneda embedding".
mentioned at the end of the main article is often called the "Yoneda embedding".
References
| [a1] | B. Mitchell, "Theory of categories" , Acad. Press (1965) |
| [a2] | J. Adámek, "Theory of mathematical structures" , Reidel (1983) |
Functor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Functor&oldid=38448