Fourier series
of a function 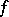 in a system of functions
in a system of functions  which are orthonormal on an interval
which are orthonormal on an interval 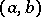
The series
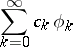 |
whose coefficients are determined by
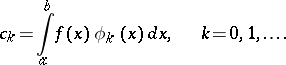 | (1) |
These coefficients are called the Fourier coefficients of 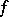 . In general it is assumed that
. In general it is assumed that 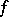 is square integrable on
is square integrable on 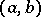 . For many systems
. For many systems 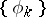 this requirement can be relaxed by replacing it by another which ensures the existence of all the integrals in (1).
this requirement can be relaxed by replacing it by another which ensures the existence of all the integrals in (1).
The Fourier series in the trigonometric system is defined for every function 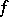 that is integrable on
that is integrable on 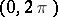 . It is the series
. It is the series
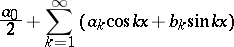 | (2) |
with coefficients
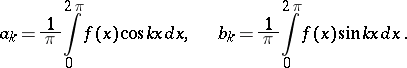 | (3) |
Fourier series for functions in several variables are constructed analogously. A further generalization leads to Fourier coefficients and Fourier series for elements of a Hilbert space.
The theory of Fourier series in the trigonometric system has been most thoroughly developed, and these were the first examples of Fourier series. If one has in mind Fourier series in the trigonometric system, it is usual to talk simply of Fourier series, without indicating the system by which they are constructed.
Fourier series form a considerable part of the theory of trigonometric series. Fourier series first appeared in the papers of J. Fourier (1807) devoted to an investigation of the problems of heat conduction. He suggested representing a function  given on
given on 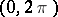 by the trigonometric series (2) with coefficients determined by (3). Such a choice of coefficients is natural from many points of view. For example, if the series (2) converges uniformly to
by the trigonometric series (2) with coefficients determined by (3). Such a choice of coefficients is natural from many points of view. For example, if the series (2) converges uniformly to  , then term-by-term integration leads to the expressions for the coefficients
, then term-by-term integration leads to the expressions for the coefficients 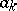 and
and 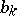 given in (3). These formulas had been obtained already by L. Euler (1777) by term-by-term integration.
given in (3). These formulas had been obtained already by L. Euler (1777) by term-by-term integration.
Using (3) the Fourier series (2) can be constructed for every function that is integrable over  . Integrability of the function can be understood in various senses, for example integrability according to Riemann or Lebesgue. Depending on this, one speaks of Fourier–Riemann series, Fourier–Lebesgue series, etc. The concepts of the Riemann and the Lebesgue integral themselves arose to a considerable extent in connection with research on Fourier series. The modern presentation of the theory of Fourier series was developed after the construction of the Lebesgue integral, and since then it has developed mainly as the theory of Fourier–Lebesgue series. Below it is assumed that the function
. Integrability of the function can be understood in various senses, for example integrability according to Riemann or Lebesgue. Depending on this, one speaks of Fourier–Riemann series, Fourier–Lebesgue series, etc. The concepts of the Riemann and the Lebesgue integral themselves arose to a considerable extent in connection with research on Fourier series. The modern presentation of the theory of Fourier series was developed after the construction of the Lebesgue integral, and since then it has developed mainly as the theory of Fourier–Lebesgue series. Below it is assumed that the function 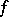 has period
has period 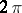 and is Lebesgue integrable over the period.
and is Lebesgue integrable over the period.
In the theory of Fourier series one studies the relation between the properties of functions and the properties of their Fourier series; in particular, one investigates questions on the representation of functions by Fourier series.
The proof of a minimum property of the partial sums of Fourier series goes back to the work of F. Bessel (1828): Given an 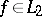 , then among all the trigonometric polynomials of order
, then among all the trigonometric polynomials of order  ,
,
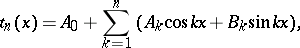 |
the smallest value of the integral
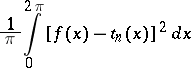 |
is attained for the partial sum of the Fourier series (2) of 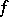 :
:
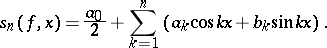 |
This smallest value is equal to
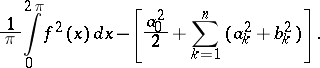 |
This implies the Bessel inequality
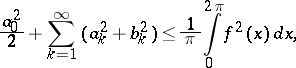 |
which is satisfied for every function 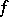 in
in 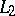 .
.
The system of trigonometric functions is a closed system (cf. Closed system of elements (functions)), that is, if 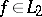 , then the Parseval equality
, then the Parseval equality
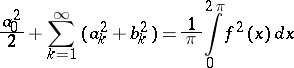 |
is valid, where 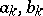 are the Fourier coefficients of
are the Fourier coefficients of 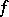 . In particular, for functions
. In particular, for functions 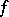 in
in 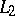 the series
the series
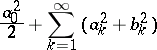 | (4) |
is convergent. The converse assertion also holds: If for a system of numbers 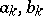 the series (4) converges, then these numbers are the Fourier coefficients of a certain function
the series (4) converges, then these numbers are the Fourier coefficients of a certain function  (F. Riesz and E. Fischer, 1907).
(F. Riesz and E. Fischer, 1907).
The Fourier coefficients of any integrable function tend to zero. This statement is called the Riemann–Lebesgue theorem. B. Riemann proved it for Fourier–Riemann series and e dimension','../l/l057830.htm','Lebesgue function','../l/l057840.htm','Lebesgue inequality','../l/l057850.htm','Lebesgue integral','../l/l057860.htm','Lebesgue measure','../l/l057870.htm','Lebesgue summation method','../l/l057940.htm','Lebesgue theorem','../l/l057950.htm','Measure','../m/m063240.htm','Metric space','../m/m063680.htm','Metric theory of functions','../m/m063700.htm','Orthogonal series','../o/o070370.htm','Perron method','../p/p072370.htm','Potential theory','../p/p074140.htm','Regular boundary point','../r/r080680.htm','Singular integral','../s/s085570.htm','Suslin theorem','../s/s091480.htm','Urysohn–Brouwer lemma','../u/u095860.htm','Vitali variation','../v/v096790.htm')" style="background-color:yellow;">H. Lebesgue for Fourier–Lebesgue series.
If the function 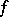 is absolutely continuous, then the Fourier series for the derivative
is absolutely continuous, then the Fourier series for the derivative 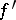 can be obtained by term-by-term differentation of the Fourier series for
can be obtained by term-by-term differentation of the Fourier series for 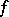 . This implies that if the derivative of order
. This implies that if the derivative of order 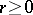 of a function
of a function 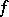 is absolutely continuous, then the estimates
is absolutely continuous, then the estimates
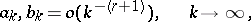 |
are valid for the Fourier coefficients of 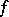 .
.
The first convergence criterion for Fourier series was obtained by P.G.L. Dirichlet in 1829. His result (the Dirichlet theorem) can be formulated as follows: If a function 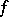 has a finite number of maxima and minima over the period and is everywhere continuous, except at a finite number of points where it may have discontinuities of the first kind, then the Fourier series of
has a finite number of maxima and minima over the period and is everywhere continuous, except at a finite number of points where it may have discontinuities of the first kind, then the Fourier series of 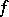 converges for all
converges for all  , and, moreover, at points of continuity it converges to
, and, moreover, at points of continuity it converges to 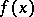 and at points of discontinuity it converges to
and at points of discontinuity it converges to  . Subsequently, this assertion was extended to arbitrary functions of bounded variation (C. Jordan, 1881).
. Subsequently, this assertion was extended to arbitrary functions of bounded variation (C. Jordan, 1881).
According to the localization principle proved by Riemann (1853), the convergence or divergence of the Fourier series of a function 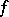 at a point
at a point  , and the value of the sum when it converges, depends only on the behaviour of
, and the value of the sum when it converges, depends only on the behaviour of 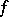 in an arbitrarily small neighbourhood of
in an arbitrarily small neighbourhood of  .
.
Many different convergence criteria for Fourier series at a point are known. R. Lipschitz (1864) established that the Fourier series of a function 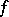 converges at a point
converges at a point  if
if 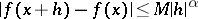 is satisfied for all sufficiently small
is satisfied for all sufficiently small 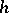 , where
, where 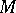 and
and 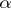 are certain positive constants (the Lipschitz criterion). The Dini criterion is more general: The Fourier series of a function
are certain positive constants (the Lipschitz criterion). The Dini criterion is more general: The Fourier series of a function 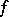 converges to
converges to 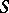 at a point
at a point  if the integral
if the integral
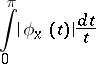 |
converges, where 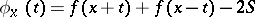 . The value
. The value 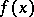 is usually taken for
is usually taken for 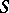 . For example, if the Fourier series of
. For example, if the Fourier series of 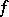 converges at a point
converges at a point  where this function is continuous, then the sum of the series is necessarily equal to
where this function is continuous, then the sum of the series is necessarily equal to 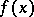 .
.
Lebesgue (1905) proved that if
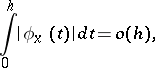 |
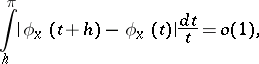 |
as 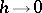 , then the Fourier series of
, then the Fourier series of 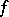 converges to
converges to 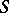 at
at  . This Lebesgue criterion is stronger than all those given above and stronger than the de la Vallée-Poussin criterion and the Young criterion. But verifying it is usually difficult.
. This Lebesgue criterion is stronger than all those given above and stronger than the de la Vallée-Poussin criterion and the Young criterion. But verifying it is usually difficult.
A convergence criterion of another type is given by the Hardy–Littlewood theorem (1932): The Fourier series of a function 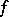 converges at a point
converges at a point  if the following conditions are satisfied:
if the following conditions are satisfied:
1)
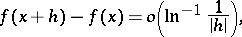 |
as 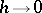 ; and
; and
2) the estimates
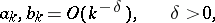 |
are valid for the Fourier coefficients of 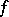 .
.
Besides convergence criteria for Fourier series at a point, criteria for uniform convergence have been studied also. Let a function 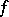 have period
have period 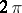 and be continuous. Then its Fourier series converges uniformly to it on the whole real line if the modulus of continuity (cf. Continuity, modulus of)
and be continuous. Then its Fourier series converges uniformly to it on the whole real line if the modulus of continuity (cf. Continuity, modulus of) 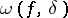 of
of 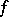 satisfies the condition
satisfies the condition
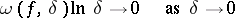 |
(the Dini–Lipschitz criterion) or if 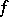 has bounded variation (the Jordan criterion).
has bounded variation (the Jordan criterion).
From this one can obtain criteria for uniform convergence of Fourier series on a certain interval if the localization principle for uniform convergence is used. The latter is formulated as follows. If two functions are equal on an interval 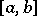 , then on each strictly interior interval
, then on each strictly interior interval  ,
, 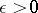 , either the Fourier series of these functions are both uniformly convergent or neither is uniformly convergent. In other words, the uniform convergence of the Fourier series of a function
, either the Fourier series of these functions are both uniformly convergent or neither is uniformly convergent. In other words, the uniform convergence of the Fourier series of a function 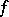 on an interval depends only on the behaviour of
on an interval depends only on the behaviour of 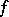 in an arbitrarily small extension of this interval.
in an arbitrarily small extension of this interval.
P. du Bois-Reymond (1876) established that the continuity of a function at a certain point does not guarantee that its Fourier series converges at this point. Later it was proved that the Fourier series of a continuous function may diverge on an everywhere-dense set of measure zero that is of the second category.
If nothing is assumed about the function except that it is integrable, then its Fourier series may turn out to be divergent almost-everywhere, or even everywhere. The first examples of such functions were constructed by A.N. Kolmogorov (1923, 1926). Later it was shown that this may be true both for the Fourier series of the function itself and for the function conjugate to it.
As early as 1915, N.N. Luzin made the conjecture that the Fourier series of every 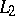 -function converges almost-everywhere. For a long time only partial results were obtained in this direction. The general form of the problem turned out to be very difficult and it was only in 1966 that L. Carleson proved the validity of this conjecture (see Carleson theorem). The Fourier series of
-function converges almost-everywhere. For a long time only partial results were obtained in this direction. The general form of the problem turned out to be very difficult and it was only in 1966 that L. Carleson proved the validity of this conjecture (see Carleson theorem). The Fourier series of 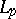 -functions when
-functions when 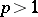 also converge almost-everywhere. Kolmogorov's example shows that it is impossible to strengthen this result any further in terms of the spaces
also converge almost-everywhere. Kolmogorov's example shows that it is impossible to strengthen this result any further in terms of the spaces 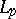 .
.
Since the partial sums of a Fourier series do not always converge, one also considers the summation of Fourier series by some average of the partial sums and uses this to represent the function. One of the simplest examples are the Fejér sums (cf. Fejér sum), which are the arithmetical means of the partial sums 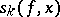 of the Fourier series:
of the Fourier series:
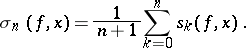 |
For every integrable function 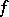 the sums
the sums 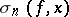 converge to
converge to 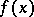 almost-everywhere and, moreover, converge at every point where
almost-everywhere and, moreover, converge at every point where 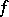 is continuous; if
is continuous; if 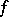 is continuous everywhere, then they converge uniformly.
is continuous everywhere, then they converge uniformly.
According to the Denjoy–Luzin theorem, if the trigonometric series (2) at every  converges absolutely on a set of positive measure, then the series
converges absolutely on a set of positive measure, then the series
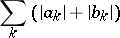 | (5) |
converges, and hence the series (2) converges absolutely for all  . Thus, the absolute convergence of (2) is equivalent to convergence of (5).
. Thus, the absolute convergence of (2) is equivalent to convergence of (5).
e theorem','../l/l057530.htm','Lebesgue constants','../l/l057800.htm','Limit theorems','../l/l058920.htm','Lyapunov theorem','../l/l061200.htm','Markov–Bernstein-type inequalities','../m/m110060.htm','Orthogonal polynomials','../o/o070340.htm')" style="background-color:yellow;">S.N. Bernstein [S.N. Bernshtein] (1934) proved that if the modulus of continuity 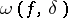 of a function
of a function 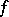 satisfies
satisfies
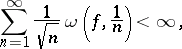 |
then the Fourier series of 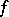 converges absolutely. It is impossible to weaken this condition: If
converges absolutely. It is impossible to weaken this condition: If 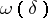 is a modulus of continuity of function type such that the series
is a modulus of continuity of function type such that the series
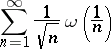 |
diverges, then a function  can be found with modulus of continuity satisfying
can be found with modulus of continuity satisfying  and whose Fourier series does not converge absolutely.
and whose Fourier series does not converge absolutely.
In particular, the Fourier series of functions satisfying a Lipschitz condition of order  converge absolutely. When
converge absolutely. When 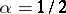 , absolute convergence need not hold (Bernshtein, 1914).
, absolute convergence need not hold (Bernshtein, 1914).
If 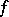 is a function of bounded variation and if its modulus of continuity satisfies
is a function of bounded variation and if its modulus of continuity satisfies
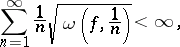 | (6) |
then the Fourier series of 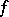 converges absolutely (see [9]). Condition (6) cannot be weakened (see [10]).
converges absolutely (see [9]). Condition (6) cannot be weakened (see [10]).
In contrast to the above, the following theorem gives a criterion for the absolute convergence for an individual function. A necessary and sufficient condition for the absolute convergence of the Fourier series of a function 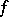 is that the series
is that the series
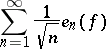 |
converges, where 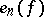 is the best approximation to
is the best approximation to 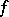 in the metric of
in the metric of 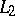 by trigonometric polynomials containing
by trigonometric polynomials containing  harmonics (see [11]).
harmonics (see [11]).
The series (2) can be considered as the real part of the power series
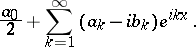 |
The imaginary part
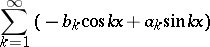 | (7) |
is called the series conjugate to the series (2).
Let 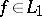 and let (2) be its Fourier series. Then for almost-all
and let (2) be its Fourier series. Then for almost-all  the function
the function
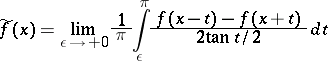 |
exists (I.I. Privalov, 1919). The function 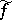 is called the conjugate function to
is called the conjugate function to 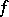 ; it need not be integrable. However, if
; it need not be integrable. However, if 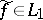 , then the Fourier series of
, then the Fourier series of 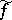 is the series (7) (V.I. Smirnov, 1928).
is the series (7) (V.I. Smirnov, 1928).
In many cases one can deduce some property or other of the conjugate series (7) from the properties of the function 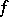 or its Fourier series (2), for example, convergence in the metric of
or its Fourier series (2), for example, convergence in the metric of 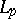 , convergence or summability at a point, or almost-everywhere, etc.
, convergence or summability at a point, or almost-everywhere, etc.
Properties of Fourier series under special assumptions on their coefficients have also been studied. For example, lacunary trigonometric series, when the only non-zero coefficients are those indexed by numbers 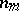 forming a lacunary sequence, that is,
forming a lacunary sequence, that is, 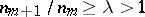 . Another example of special series are series with monotone coefficients.
. Another example of special series are series with monotone coefficients.
All that has been said above concerns Fourier series of the form (2). For Fourier series in a rearranged trigonometric system certain properties of the Fourier series in the trigonometric system, taken in the usual order, do not hold. For example, there is a continuous function such that its Fourier series after a certain rearrangement diverges almost-everywhere (see [12]–[15]).
The theory of Fourier series for functions in several variables (multiple Fourier series) has been developed to a lesser extent. Some of the multi-dimensional results are analogous to the one-dimensional results. But there are crucial differences.
Let 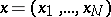 be a point of the
be a point of the 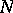 -dimensional space, let
-dimensional space, let  be an
be an 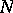 -dimensional vector with integer coordinates and let
-dimensional vector with integer coordinates and let 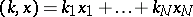 . For a function
. For a function 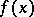 with period
with period 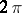 in each variable and Lebesgue integrable over the
in each variable and Lebesgue integrable over the 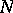 -dimensional cube
-dimensional cube 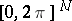 , the Fourier series in the trigonometric system is
, the Fourier series in the trigonometric system is
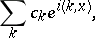 | (8) |
where the summation is over all  and
and
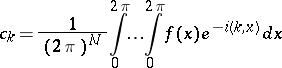 |
are the Fourier coefficients of  . The Fourier series (8) is written in complex form. Writing it in trigonometric form as a series in the products of multiple cosines and sines is rather more clumsy.
. The Fourier series (8) is written in complex form. Writing it in trigonometric form as a series in the products of multiple cosines and sines is rather more clumsy.
Various definitions of the partial sums of the series (8) are possible; for example, partial sums over rectangles
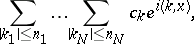 |
and over circles
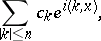 | (9) |
where  is the radius and
is the radius and 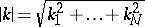 .
.
The circular partial sums (9) are not so suitable for representing functions as are their Riesz means
 |
For Riesz means of order  of Fourier series of
of Fourier series of 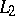 -functions the localization principle is valid; this is not so for smaller
-functions the localization principle is valid; this is not so for smaller  (S. Bochner, 1936). The Riesz means of circular partial sums of critical order
(S. Bochner, 1936). The Riesz means of circular partial sums of critical order 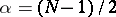 play an essential role also in other questions about Fourier series of functions in several variables.
play an essential role also in other questions about Fourier series of functions in several variables.
There is a continuous function in two variables with a Fourier series that does not converge over rectangles at any interior point of the square 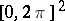 (see [16]).
(see [16]).
Certain results about Fourier series in the trigonometric system can be generalized considerably; for example, they can be carried over in a corresponding way to the spectral decompositions corresponding to self-adjoint elliptic differential operators.
References
| [1] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [2] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
| [3] | G.H. Hardy, W.W. Rogosinsky, "Fourier series" , Cambridge Univ. Press (1965) |
| [4] | N.N. Luzin, "The integral and trigonometric series" , Moscow-Leningrad (1951) (In Russian) (Thesis; also: Collected Works, Vol. 1, Moscow, 1953, pp. 48–212) |
| [5] | H. Lebesgue, "Leçons sur les séries trigonométriques" , Gauthier-Villars (1906) |
| [6] | A.B. Paplauskas, "Trigonometric series from Euler to Lebesgue" , Moscow (1966) (In Russian) |
| [7] | P.L. Ul'yanov, "Solved and unsolved problems in the theory of trigonometric and orthogonal series" Russian Math. Surveys , 19 : 1 (1964) pp. 1–62 Uspekhi Mat. Nauk , 19 : 1 (1964) pp. 3–69 |
| [8] | Sh.A. Alimov, V.A. Il'in, E.M. Nikishin, "Convergence problems of multiple trigonometric series and spectral decomposition. I" Russian Math. Surveys , 31 : 6 (1976) pp. 29–86 Uspekhi Mat. Nauk , 31 : 6 (1976) pp. 28–83 |
| [9] | R. Salem, "On a theorem of Zygmund" Duke Math. J. , 10 (1943) pp. 23–31 |
| [10] | S.V. Bochkarev, "On a problem of Zygmund" Math. USSR Izv. , 7 : 3 (1973) pp. 629–637 Izv. Akad. Nauk SSSR , 37 (1973) pp. 630–638 |
| [11] | S.B. Stechkin, "On absolute convergence of orthogonal series" Dokl. Akad. Nauk SSSR , 102 (1955) pp. 37–40 (In Russian) |
| [12] | A.N. [A.N. Kolmogorov] Kolmogoroff, D.E. [D.E. Menshov] Menschoff, "Sur la convergence des séries de fonctions orthogonales" Math. Z. , 26 (1927) pp. 432–441 |
| [13] | Z. Zahorski, "Une série de Fourier permutée d'une fonction de classe 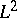 divergente partout" C.R. Acad. Sci. Paris , 251 (1960) pp. 501–503 divergente partout" C.R. Acad. Sci. Paris , 251 (1960) pp. 501–503 |
| [14] | P.L. Ul'yanov, "Divergent Fourier series" Russian Math. Surveys , 16 : 3 (1961) pp. 1–75 Uspekhi Mat. Nauk , 16 : 3 (1961) pp. 61–142 |
| [15] | A.M. Olevskii, "Divergent Fourier series for continuous functions" Soviet Math. Dokl. , 2 (1961) pp. 1382–1386 Dokl. Akad. Nauk SSSR , 141 (1961) pp. 28–31 |
| [16] | C. Fefferman, "On the divergence of multiple Fourier series" Bull. Amer. Math. Soc. , 77 (1971) pp. 191–195 |
Comments
A closed system is also called a complete system (cf. Complete system of functions). Instead of Riemann–Lebesgue theorem one often uses Riemann–Lebesgue lemma.
For multiple Fourier series see, e.g., Chapt. 7 of [a5].
References
| [a1] | R.E. Edwards, "Fourier series. A modern introduction" , 1–2 , Springer (1979–1982) |
| [a2] | J.-P. Kahane, "Séries de Fourier absolument convergentes" , Springer (1970) |
| [a3] | Y. Katznelson, "An introduction to harmonic analysis" , Wiley (1968) |
| [a4] | H. Dym, H.P. McKean, "Fourier series and integrals" , Acad. Press (1972) |
| [a5] | E.M. Stein, G. Weiss, "Introduction to Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1971) |
Fourier series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier_series&oldid=18983