Fourier method
method of separation of variables
A method for finding particular solutions of differential equations
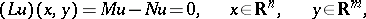 | (1) |
where 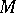 (respectively,
(respectively, 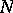 ) are linear differential expressions containing only derivatives with respect to the variables
) are linear differential expressions containing only derivatives with respect to the variables  (respectively,
(respectively, 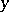 ) with coefficients also depending only on
) with coefficients also depending only on  (respectively,
(respectively, 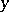 ). A function
). A function
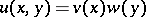 | (2) |
is a solution of (1) if there is a constant 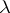 such that
such that
 | (3) |
For example, for the equation of a vibrating string
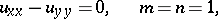 | (4) |
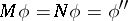 , and the solution (2) takes the form
, and the solution (2) takes the form
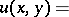 | (5) |
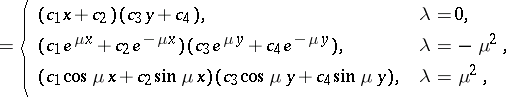 |
where 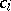 ,
, 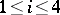 , are arbitrary constants and
, are arbitrary constants and 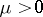 . The solutions (5) satisfy the boundary conditions
. The solutions (5) satisfy the boundary conditions
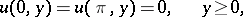 | (6) |
when  ,
, 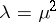 ,
, 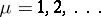 . The so-called Fourier series composed of these functions,
. The so-called Fourier series composed of these functions,
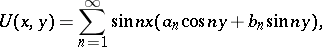 | (7) |
gives the solution of the initial-boundary value problem (4), (6) and initial condition
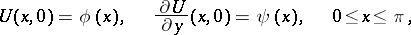 | (8) |
if 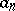 and
and 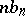 are the Fourier coefficients
are the Fourier coefficients
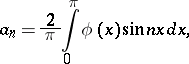 |
 |
of the data 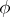 and
and 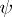 which are assumed to be sufficiently smooth. In a similar way solutions of initial-boundary value problems can be obtained for more general classes of equations (1), where the role of the theory of Fourier series associated with the expansion (7) is played by the spectral theory of linear operators.
which are assumed to be sufficiently smooth. In a similar way solutions of initial-boundary value problems can be obtained for more general classes of equations (1), where the role of the theory of Fourier series associated with the expansion (7) is played by the spectral theory of linear operators.
The Fourier method is closely connected with the special functions solving equations (3) for particular cases of operators 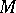 and
and 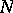 ,
, 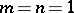 . Many of these functions originally arose in this way. For example, when applying this method to the Helmholtz equation
. Many of these functions originally arose in this way. For example, when applying this method to the Helmholtz equation
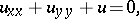 |
one obtains after transition to polar coordinates
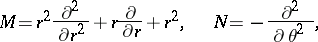 |
and the first equation in (3) becomes the Bessel differential equation.
Generally speaking, a differential equation has a whole family of coordinate systems in which it admits separation of variables, that is, reduces to the form (1). The problem of finding such coordinate systems is closely connected with group properties of differential equations. Applying methods from the theory of Lie groups enables one to describe all the separable solutions of many classical equations in mathematical physics (those of Laplace, Helmholtz and Schrödinger, the wave equation, etc.). In this way also a whole series of relations is obtained in the theory of special functions.
The method of separation of variables was suggested by J. d'Alembert (1749) for solving the wave equation, the method was developed fairly thoroughly at the beginning of the 19th century by J. Fourier and was formulated in complete generality by M.V. Ostrogradski in 1828.
References
| [1] | A.V. Bitsadze, "Equations of mathematical physics" , MIR (1980) (Translated from Russian) |
| [2] | U. Miller, "Symmetry and separation of variables" , Addison-Wesley (1977) |
Comments
References
| [a1] | G.W. Bluman, G.D. Cole, "Similarity methods for differential equations" , Springer (1974) |
Fourier method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier_method&oldid=13168