Form of an algebraic group
 defined over a field
defined over a field 
An algebraic group  defined over
defined over  and isomorphic to
and isomorphic to  over some extension
over some extension  of
of  . In this case
. In this case 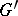 is called an
is called an 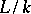 -form of
-form of 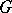 . If
. If  is the separable closure of
is the separable closure of 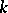 in a fixed algebraically closed ground field
in a fixed algebraically closed ground field 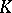 (a universal domain), then
(a universal domain), then 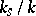 -forms are simply called
-forms are simply called 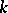 -forms of
-forms of 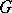 . Two
. Two 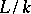 -forms of a group are said to be equivalent if they are isomorphic over
-forms of a group are said to be equivalent if they are isomorphic over  . The set of equivalence classes of
. The set of equivalence classes of 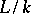 -forms of
-forms of  is denoted by
is denoted by 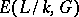 (in the case
(in the case  by
by 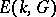 ) (see [5], [7], [8]).
) (see [5], [7], [8]).
Example. Let 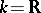 ,
, 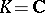 . Then
. Then
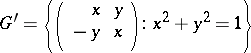 |
and
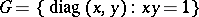 |
are two subgroups of the general linear group 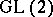 defined over
defined over 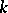 , and
, and  is a
is a 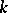 -form of
-form of 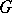 (the isomorphism
(the isomorphism 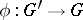 , defined over
, defined over 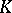 , is given by the formula
, is given by the formula
 |
This 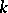 -form is not equivalent to
-form is not equivalent to 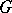 (if one regards
(if one regards  as a
as a 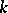 -form of itself relative to the identity isomorphism
-form of itself relative to the identity isomorphism 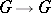 ). In this example, the set
). In this example, the set  consists of the two elements represented by the two
consists of the two elements represented by the two  -forms above.
-forms above.
The problem of classifying forms of algebraic groups can be naturally reformulated in the language of Galois cohomology, [3], [5]. Namely, suppose that 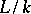 is a Galois extension with Galois group
is a Galois extension with Galois group  (equipped with the Krull topology). The group
(equipped with the Krull topology). The group 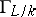 acts naturally on the group
acts naturally on the group 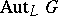 of all
of all 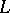 -automorphisms of
-automorphisms of 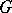 , and also on the set of all
, and also on the set of all 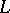 -isomorphisms from
-isomorphisms from 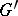 to
to 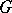 (in coordinates, these actions reduce to applying the automorphisms in
(in coordinates, these actions reduce to applying the automorphisms in 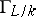 to the coefficients of the rational functions defining the respective mappings). Let
to the coefficients of the rational functions defining the respective mappings). Let  be some
be some 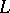 -isomorphism, let
-isomorphism, let 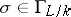 and let
and let 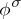 be the image of
be the image of 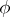 under the action of
under the action of  . Then the mapping
. Then the mapping 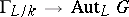 ,
,  , is a continuous
, is a continuous 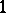 -cocycle of
-cocycle of 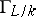 with values in the discrete group
with values in the discrete group  . When replacing
. When replacing 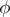 by another
by another 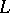 -isomorphism
-isomorphism 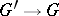 , this cocycle changes to a cocycle in the same cohomology class. Thus arises a mapping
, this cocycle changes to a cocycle in the same cohomology class. Thus arises a mapping  . The main importance of the cohomological interpretation of the forms of
. The main importance of the cohomological interpretation of the forms of 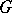 consists in the fact that this mapping is bijective. In the case when all automorphisms
consists in the fact that this mapping is bijective. In the case when all automorphisms 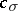 are inner,
are inner,  is called an inner form of
is called an inner form of 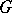 , and otherwise an outer form.
, and otherwise an outer form.
For connected reductive groups there is a thoroughly developed theory of forms, where relative versions of the structure theory of linear algebraic groups over an algebraically closed field are established: 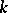 -roots, the
-roots, the 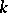 -Weyl group, the Bruhat decomposition over
-Weyl group, the Bruhat decomposition over 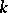 , etc. Here the role of maximal tori is played by maximal
, etc. Here the role of maximal tori is played by maximal  -split tori, and that of Borel subgroups by minimal
-split tori, and that of Borel subgroups by minimal 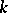 -parabolic subgroups [1], [2], , [7]. This theory enables one to reduce the question of classifying forms to that of classifying anisotropic reductive groups over
-parabolic subgroups [1], [2], , [7]. This theory enables one to reduce the question of classifying forms to that of classifying anisotropic reductive groups over 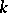 (see Anisotropic group; Anisotropic kernel). The question of classifying the latter depends essentially on the properties of the field
(see Anisotropic group; Anisotropic kernel). The question of classifying the latter depends essentially on the properties of the field 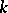 . If
. If  and
and 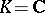 , then the characterization of forms of semi-simple algebraic groups is the same as that of real forms of complex semi-simple algebraic groups (see Complexification of a Lie group).
, then the characterization of forms of semi-simple algebraic groups is the same as that of real forms of complex semi-simple algebraic groups (see Complexification of a Lie group).
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [2] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) |
| [3] | J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964) |
| [4] | J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959) |
| [5] | V.E. Voskresenskii, "Algebraic tori" , Moscow (1977) (In Russian) |
| [6a] | A. Borel, J. Tits, "Groupes réductifs" Publ. Math. IHES , 27 (1965) pp. 55–150 |
| [6b] | A. Borel, J. Tits, "Complement à l'article "Groupes réductifs" " Publ. Math. IHES , 41 (1972) pp. 253–276 |
| [7] | J. Tits, "Classification of algebraic semi-simple groups" , Algebraic Groups and Discontinuous Subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 33–62 |
| [8] | T.A. Springer, "Reductive groups" , Proc. Symp. Pure Math. , 33 : 1 , Amer. Math. Soc. (1979) pp. 3–27 |
| [9] | J.-P. Serre, "Local fields" , Springer (1979) (Translated from French) |
Comments
References
| [a1] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , Masson (1970) |
| [a2] | J.C. Jantzen, "Representations of algebraic groups" , Acad. Press (1987) |
Form of an algebraic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Form_of_an_algebraic_group&oldid=17664