Flat form
A measurable  -dimensional differential form
-dimensional differential form 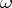 on an open set
on an open set 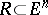 such that: 1) the co-mass (cf. Mass and co-mass)
such that: 1) the co-mass (cf. Mass and co-mass) 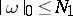 for a given
for a given 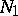 ; and 2) there exists an
; and 2) there exists an  with
with
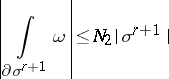 |
for any simplex 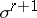 satisfying the following condition: There exists a measurable
satisfying the following condition: There exists a measurable 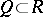 ,
, 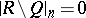 , such that
, such that 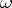 is measurable on
is measurable on 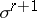 and on any one of its boundaries
and on any one of its boundaries 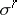 , making up
, making up 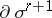 ; moreover,
; moreover,
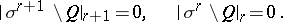 |
Here, 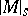 denotes the
denotes the  -dimensional Lebesgue measure of the intersection of the set
-dimensional Lebesgue measure of the intersection of the set 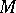 with some
with some  -dimensional plane.
-dimensional plane.
If 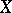 is an
is an  -dimensional flat cochain in
-dimensional flat cochain in 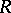 , there exists a bounded
, there exists a bounded  -dimensional form
-dimensional form 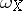 in
in 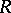 which is measurable in any simplex
which is measurable in any simplex 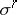 with respect to the plane which contains
with respect to the plane which contains 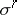 , and
, and
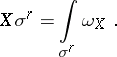 | (1) |
Also
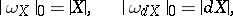 |
where  is the co-mass of the cochain
is the co-mass of the cochain 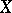 . Conversely, to any
. Conversely, to any  -dimensional flat form
-dimensional flat form 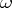 in
in 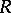 there corresponds, according to formula (1), a unique
there corresponds, according to formula (1), a unique  -dimensional flat cochain
-dimensional flat cochain 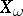 for any simplex
for any simplex 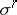 which satisfies the above condition; moreover,
which satisfies the above condition; moreover,
 |
The form 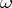 and the cochain
and the cochain  are called associated. Forms associated with the same cochain are equivalent, i.e. are equal almost-everywhere in
are called associated. Forms associated with the same cochain are equivalent, i.e. are equal almost-everywhere in 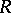 , and comprise the flat representative.
, and comprise the flat representative.
There is a one-to-one correspondence between the  -dimensional flat cochains
-dimensional flat cochains 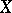 and the classes of equivalent bounded measurable functions
and the classes of equivalent bounded measurable functions 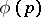 , given by
, given by 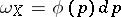 , and
, and
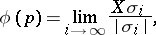 |
where 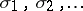 is a sequence of
is a sequence of  -dimensional simplices contracting towards the point
-dimensional simplices contracting towards the point  such that their diameters tend to zero, but such that
such that their diameters tend to zero, but such that
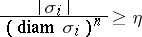 |
for some value of  , where
, where 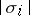 is the volume
is the volume 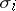 for all
for all 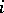 .
.
Let 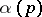 be a measurable summable function in
be a measurable summable function in 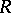 whose values are
whose values are  -vectors; it is said to correspond to an
-vectors; it is said to correspond to an  -dimensional flat chain if
-dimensional flat chain if
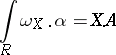 | (2) |
for all  -dimensional flat cochains
-dimensional flat cochains 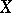 (
(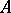 is then called a Lebesgue chain). The mapping
is then called a Lebesgue chain). The mapping  is a linear one-to-one mapping of the set of equivalence classes of functions
is a linear one-to-one mapping of the set of equivalence classes of functions 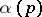 into the space of flat chains
into the space of flat chains 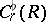 ; also,
; also,  , where
, where 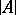 is the mass of the chain
is the mass of the chain 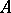 , (cf. Mass and co-mass) and
, (cf. Mass and co-mass) and 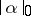 is the mass of the
is the mass of the  -vector
-vector  . In addition, the set of images of continuous functions
. In addition, the set of images of continuous functions  is dense in
is dense in 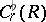 .
.
Formulas (1) and (2) generalize similar results for sharp forms and sharp cochains (cf. Sharp form); for instance, the differential of the flat form 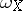 , defined by the formula
, defined by the formula 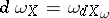 , is also a flat form, and Stokes' theorem:
, is also a flat form, and Stokes' theorem: 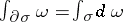 is valid for any simplex
is valid for any simplex  ; an
; an  -dimensional flat cochain is the weak limit of smooth cochains, i.e. cochains for which the associated forms
-dimensional flat cochain is the weak limit of smooth cochains, i.e. cochains for which the associated forms 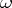 are smooth, etc.
are smooth, etc.
References
| [1] | H. Whitney, "Geometric integration theory" , Princeton Univ. Press (1957) |
Flat form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flat_form&oldid=18201