Difference between revisions of "Finiteness theorems"
Ulf Rehmann (talk | contribs) m (tex done) |
Ulf Rehmann (talk | contribs) m (tex done) |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{TEX|done}} | {{TEX|done}} | ||
Latest revision as of 20:08, 17 December 2019
A finiteness theorem in algebraic geometry is an assertion about the various objects in algebraic geometry (cohomology spaces, algebraic varieties, schemes, fibrations, etc.), stating that these objects depend on finitely many parameters or even form finite sets.
The first circle of finiteness theorems relates to cohomology spaces of coherent algebraic sheaves. The fundamental theorem states that these spaces are finite-dimensional over the ground field $ k $ if the variety is proper (for $ k = \mathbf C $ this property is equivalent to compactness) (see [2]). Far-reaching generalizations of this theorem have been obtained in the theory of schemes. One of them generalizes the theorem to the case of proper morphisms of schemes and asserts that the direct image of a coherent sheaf under such a mapping is coherent (see [3], [4]). Another generalization relates to the study of the cohomology of improper varieties. It turns out that if the variety $ X $ under discussion is obtained by the excision of some subvariety $ Y $ from a proper variety, then it is possible to estimate the dimensions in which the cohomology groups are finite-dimensional. These estimates depend on the codimension of $ Y $ and on properties of its singular points (see [5], [6]). Corresponding results are known for étale cohomology.
Another circle of finiteness theorems relates to subschemes and, more generally, to coherent sheaves over a fixed proper scheme. These objects can be parametrized in a very general situation by Hilbert schemes (or by Picard schemes in the case of invertible sheaves, cf. Hilbert scheme; Picard scheme). The most general of these finiteness theorems asserts that such schemes are quasi-projective if one restricts oneself to subschemes or to sheaves with one and the same Hilbert polynomial [4]. A special case is the fact that algebraic subvarieties of given degree in a projective space depend on finitely many parameters, as well as the theorem stating that the Néron–Severi group has a finite basis.
These theorems find application in a wide range of finiteness problems that arise in Diophantine geometry. Among them are: the question of the finiteness of the set of rational points of an algebraic variety defined over a global field (the multi-dimensional analogue of the Mordell conjecture); Shafarevich's conjecture concerning the finiteness of the number of algebraic curves defined over a given global field and with fixed degeneracies; and the question about the finite generation of the group of rational points of an algebraic group.
References
| [1] | J.-P. Serre, "Sur la cohomologie des variétés algébriques" J. Math. Pures Appl. , 36 : 5 (1957) pp. 1–16 MR0083813 Zbl 0078.34604 |
| [2] | J.-P. Serre, "Faisceaux algébriques coherents" Ann. of Math. , 61 (1955) pp. 197–238 MR0068874 Zbl 0067.16201 |
| [3] | A. Grothendieck, "Eléments de géométrie algébrique III" Publ. Math. IHES , 17 (1963) pp. Chapt. 3, Part 2 MR0163911 Zbl 0118.36206 |
| [4] | A. Grothendieck, "Fondements de la géométrie algébrique" , Secr. Math. Univ. Paris (1961/62) (Extracts Sem. Bourbaki 1957–1962) MR1611235 MR1086880 MR0146040 Zbl 0239.14002 Zbl 0239.14001 |
| [5] | R. Hartshorne, "Ample subvarieties of algebraic varieties" , Springer (1970) MR0282977 Zbl 0208.48901 |
| [6] | A. Ogus, "Local cohomological dimension of algebraic varieties" Ann. of Math. , 98 : 2 (1973) pp. 327–365 MR0506248 Zbl 0308.14003 |
| [7] | I.R. Shafarevich, "Algebraic number fields" , Proc. Internat. Congress mathematicians (Stockholm, 1962) , Inst. Mittag-Leffler (1963) pp. 163–176 Zbl 0199.09802 Zbl 0057.27401 |
| [8] | S.Yu. Arakelov, "Families of algebraic curves with fixed degeneracies" Math. USSR Izv. , 5 : 6 (1971) pp. 1277–1302 Izv. Akad. Nauk SSSR Ser. Math. , 35 : 6 (1971) pp. 1269–1293 MR0321933 Zbl 0248.14004 |
Comments
A major recent development is the proof by G. Faltings (cf. [a1]) of the conjectures of Mordell and Shafarevich (in the case of number fields). The functional case was settled before by S.Yu. Arakelov [8]. See [a3] for a brief description of Faltings' work. See [a4] for finiteness results for algebraic cycles.
References
| [a1] | G. Faltings, "Endlichkeitssätze für abelsche Varietäten über Zahlkörpern" Invent. Math. , 73 (1983) pp. 349–366 (Erratum: Invent. Math. f0403706.png (1984), 381) MR0718935 MR0732554 Zbl 0588.14026 |
| [a2] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 MR0463157 Zbl 0367.14001 |
| [a3] | B. Mazur, "On some of the mathematical contributions of Gerd Faltings" , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , Amer. Math. Soc. (1987) pp. 7–12 MR0934210 Zbl 0663.01002 |
| [a4] | S.L. Kleiman, "Finiteness theorem for algebraic cycles" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 1 , Gauthier-Villars (1971) pp. 445–449 MR0424807 |
Finiteness theorems in the theory of analytic spaces are criteria for the finite dimensionality of cohomology groups with values in coherent analytic sheaves (cf. Coherent analytic sheaf). The first general theorem of this kind was the Cartan–Serre finiteness theorem [1]: If $ X $ is a compact complex space and $ {\mathcal F} $ is a coherent analytic sheaf on $ X $, then the cohomology spaces $ H ^{k} (X,\ {\mathcal F} ) $ are finite-dimensional and Hausdorff for all $ k \geq 0 $. A generalization of this theorem to the case of convex-concave spaces [2], [3] asserts: If $ X $ is a strictly $ (p,\ q) $- convex-concave space (see Pseudo-convex and pseudo-concave) and $ {\mathcal F} $ is a coherent analytic sheaf on $ X $, then $ H ^{k} (X,\ {\mathcal F} ) $ is finite-dimensional for $ p \leq k \leq \mathop{\rm prof}\nolimits \ {\mathcal F} - q - 1 $ and Hausdorff for $ p \leq k \leq \mathop{\rm prof}\nolimits \ {\mathcal F} - q $, while $ H _{c} ^{k} ( X ,\ {\mathcal F} ) $ is finite-dimensional for $ q +1 \leq k \leq \mathop{\rm prof}\nolimits \ {\mathcal F} - p $ and Hausdorff for $ q + 1 \leq k \leq \mathop{\rm prof}\nolimits \ {\mathcal F} - p + 1 $.
Generalizations of the above theorems to the relative case are also finiteness theorems, that is, criteria for the coherence of the direct images of coherent sheaves. The following theorem of Grauert [4], [5] is a generalization of the Cartan–Serre theorem: If $ \pi : \ X \rightarrow Y $
is a proper analytic mapping between complex spaces and $ {\mathcal F} $
is a coherent analytic sheaf over $ X $,
then the direct images $ R ^{k} \pi _{*} {\mathcal F} $
are coherent for all $ k \geq 0 $.
This property turns out to be sufficient for $ \pi $
to be a proper mapping. Similar finiteness theorems have been proved for strictly $ p $-
convex and strictly $ q $-
concave mappings (see [6]). The analogue of Grauert's theorem has been proved also for rigid analytic spaces (cf. Rigid analytic space) over a field with a non-Archimedean valuation [7].
Closely connected with finiteness theorems are theorems about estimates for the transcendence degree of fields of meromorphic functions on various classes of complex spaces (see Siegel theorem). A simple consequence of Grauert's theorem is the following theorem of Remmert [4]: If $ \pi : \ X \rightarrow Y $ is a proper analytic mapping between complex spaces and $ Z $ is an analytic set in $ X $, then $ \pi (Z) $ is an analytic set in $ Y $. This theorem carries over to the case of rigid spaces [7].
References
| [1] | H. Cartan, J.-P. Serre, "Une théorème de finitude concernant les variétés analytiques compactes" C.R. Acad. Sci. Paris , 237 (1953) pp. 128–130 MR66010 |
| [2] | A. Andreotti, G. Grauert, "Théorèmes de finitude pour la cohomologie des espaces complexes" Bull. Soc. Math. France , 90 (1962) pp. 193–259 MR0150342 Zbl 0154.33601 Zbl 0106.05501 |
| [3] | J.P. Ramis, "Théorèmes de séparation et de finitude pour l'homologie et la cohomologie des espaces 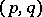 -convexes-concaves" Ann. Scuola Norm. Sup. Pisa Sci. Fis. Mat. Ser. 3 , 27 : 4 (1973) pp. 933–997 -convexes-concaves" Ann. Scuola Norm. Sup. Pisa Sci. Fis. Mat. Ser. 3 , 27 : 4 (1973) pp. 933–997 |
| [4] | G. Grauert, "Ein Theorem der analytischen Garbentheorie und die Modulräume Komplexer Strukturen" Publ. Math. IHES , 5 (1960) MR0121814 Zbl 0158.32901 Zbl 0100.08001 |
| [5] | O. Stănăşilă, "Algebraic methods in the global theory of complex spaces" , Wiley (1976) (Translated from Rumanian) MR0463470 Zbl 0334.32001 |
| [6] | A.L. Onishchik, "Pseudoconvexity in the theory of complex spaces" J. Soviet Math. , 14 : 4 (1980) pp. 1363–1428 Itogi Nauk. Algebra Topol. Geom. , 15 (1977) pp. 93–171 Zbl 0449.32020 |
| [7] | R. Kiehl, "Der Endlichkeitssatz für eigentliche Abbildungen in der nichtarchimedischen Funktionentheorie" Invent. Math. , 2 : 3 (1966) pp. 191–214 MR0210948 Zbl 0202.20101 |
A.L. Onishchik
Comments
References
| [a1] | H. Grauert, R. Remmert, "Coherent analytic sheaves" , Springer (1984) (Translated from German) MR0755331 Zbl 0537.32001 |
Finiteness theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Finiteness_theorems&oldid=44303