Fine sheaf
A sheaf of Abelian groups 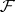 over a paracompact space
over a paracompact space 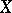 with a soft sheaf as sheaf of endomorphisms. A sheaf
with a soft sheaf as sheaf of endomorphisms. A sheaf 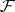 is fine if and only if for any closed subsets
is fine if and only if for any closed subsets 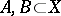 with
with 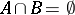 there is an endomorphism
there is an endomorphism 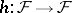 that is the identity on
that is the identity on 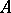 and zero on
and zero on 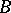 , or equivalently if for every open covering
, or equivalently if for every open covering 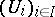 of
of 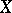 there is a locally finite collection
there is a locally finite collection 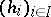 of endomorphisms of
of endomorphisms of 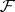 such that
such that 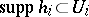
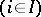 and
and 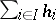 is the identity endomorphism. Every fine sheaf is soft, and if
is the identity endomorphism. Every fine sheaf is soft, and if 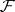 is a sheaf of rings with an identity, the converse also holds. If
is a sheaf of rings with an identity, the converse also holds. If 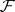 is a fine sheaf and
is a fine sheaf and  is an arbitrary sheaf of Abelian groups, then
is an arbitrary sheaf of Abelian groups, then 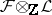 is also a fine sheaf. An example of a fine sheaf is the sheaf of germs of continuous (or differentiable of class
is also a fine sheaf. An example of a fine sheaf is the sheaf of germs of continuous (or differentiable of class 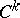 ) sections of a vector bundle over a paracompact space (respectively, over a paracompact differentiable manifold).
) sections of a vector bundle over a paracompact space (respectively, over a paracompact differentiable manifold).
References
| [1] | R. Godement, "Topologie algébrique et théorie des faisceaux" , Hermann (1958) |
| [2] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) |
Fine sheaf. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fine_sheaf&oldid=17471