Fatou theorem
in the theory of functions of a complex variable
Suppose that the harmonic function 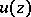 ,
, 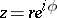 , can be represented in the unit disc
, can be represented in the unit disc 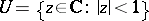 by a Poisson–Stieltjes integral
by a Poisson–Stieltjes integral
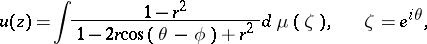 |
where 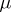 is a Borel measure concentrated on the unit circle
is a Borel measure concentrated on the unit circle 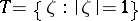 ,
, 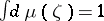 . Then almost-everywhere with respect to the Lebesgue measure on
. Then almost-everywhere with respect to the Lebesgue measure on 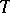 ,
, 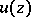 has angular boundary values (cf. Angular boundary value).
has angular boundary values (cf. Angular boundary value).
This Fatou theorem can be generalized to harmonic functions 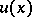 ,
,  ,
, 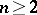 , that can be represented by a Poisson–Stieltjes integral in Lyapunov domains
, that can be represented by a Poisson–Stieltjes integral in Lyapunov domains 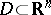 (see , ). For Fatou's theorem for radial boundary values (cf. Radial boundary value) of multiharmonic functions in the polydisc
(see , ). For Fatou's theorem for radial boundary values (cf. Radial boundary value) of multiharmonic functions in the polydisc 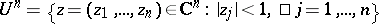 see , .
see , .
If 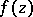 is a bounded analytic function in
is a bounded analytic function in 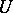 , then almost-everywhere with respect to the Lebesgue measure on
, then almost-everywhere with respect to the Lebesgue measure on 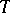 it has angular boundary values.
it has angular boundary values.
This Fatou theorem can be generalized to functions of bounded characteristic (cf. Function of bounded characteristic) (see ). Points 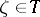 at which there is an angular boundary value
at which there is an angular boundary value 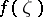 are called Fatou points. Regarding generalizations of the Fatou theorem for analytic functions
are called Fatou points. Regarding generalizations of the Fatou theorem for analytic functions 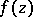 of several complex variables
of several complex variables 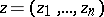 ,
,  , see ; it turns out that for
, see ; it turns out that for 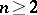 there are also boundary values along complex tangent directions.
there are also boundary values along complex tangent directions.
If the coefficients of a power series 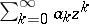 with unit disc of convergence
with unit disc of convergence 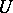 tend to zero,
tend to zero,  , then this series converges uniformly on every arc
, then this series converges uniformly on every arc 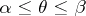 of the circle
of the circle 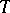 consisting only of regular boundary points for the sum of the series.
consisting only of regular boundary points for the sum of the series.
If 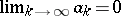 and the series converges uniformly on an arc
and the series converges uniformly on an arc 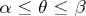 , it does not follow that the points of this arc are regular for the sum of the series.
, it does not follow that the points of this arc are regular for the sum of the series.
Theorems 1), 2) and 3) were proved by P. Fatou [1].
References
| [1] | P. Fatou, "Séries trigonométriques et séries de Taylor" Acta Math. , 30 (1906) pp. 335–400 |
| [2] | I.I. Privalov, P.I. Kuznetsov, "On boundary problems and various classes of harmonic and subharmonic functions on an arbitrary domain" Mat. Sb. , 6 : 3 (1939) pp. 345–376 (In Russian) (French summary) |
| [3] | E.D. Solomentsev, "On boundary values of subharmonic functions" Czechoslovak. Math. J. , 8 (1958) pp. 520–536 (In Russian) (French summary) |
| [4] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
| [5] | W. Rudin, "Function theory in polydiscs" , Benjamin (1969) |
| [6] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [7] | G.M. Khenkin, E.M. Chirka, "Boundary properties of holomorphic functions of several complex variables" J. Soviet Math. , 5 : 5 (1976) pp. 612–687 Itogi Nauk. i Tekhn. Sovr. Probl. Mat. , 4 (1975) pp. 13–142 |
Comments
For Lyapunov domain see Lyapunov surfaces and curves. For Fatou theorems in 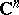 see [a3]–[a5].
see [a3]–[a5].
References
| [a1] | E. Landau, "Darstellung und Begründung einiger neuerer Ergebnisse der Funktionentheorie" , Das Kontinuum und andere Monographien , Chelsea, reprint (1973) |
| [a2] | K. Hoffman, "Banach spaces of analytic functions" , Prentice-Hall (1962) |
| [a3] | W. Rudin, "Function theory in the unit ball in 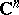 " , Springer (1980) " , Springer (1980) |
| [a4] | E.M. Stein, "Boundary behavior of holomorphic functions of several complex variables" , Princeton Univ. Press (1972) |
| [a5] | A. Nagel, E.M. Stein, "On certain maximal functions and approach regions" Adv. in Math. , 54 (1984) pp. 83–106 |
Fatou theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fatou_theorem&oldid=27214