Farey series

of order

The increasing sequence of non-negative irreducible fractions not exceeding 1 with denominators not exceeding . For example, the Farey series of order 5 is the sequence

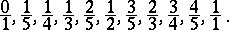The following assertions hold.

1) If 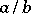and 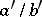are two consecutive terms of the Farey series of order , then

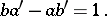2) If 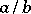, , 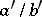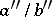are three consecutive terms of the Farey series of order , then

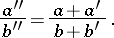3) The number of terms in the Farey series of order is equal to

(*)

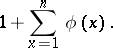Farey series were investigated by J. Farey (1816).

References

[1]	A.A. Bukhshtab, "Number theory" , Moscow (1966) (In Russian)
[2]	R.R. Hall, "A note on Farey series" J. London Math. Soc. , 2 (1970) pp. 139–148
[3]	G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979)

Comments

Of course, in (*) 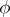denotes the Euler function.