Euler formulas
From Encyclopedia of Mathematics
Formulas connecting the exponential and trigonometric functions:
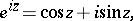 |
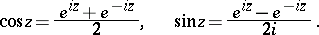 |
These hold for all values of the complex variable  . In particular, for a real value
. In particular, for a real value  the Euler formulas become
the Euler formulas become
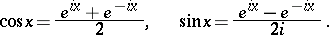 |
These formulas were published by L. Euler in [1].
References
| [1] | L. Euler, Miscellanea Berolinensia , 7 (1743) pp. 193–242 |
| [2] | L. Euler, "Einleitung in die Analysis des Unendlichen" , Springer (1983) (Translated from Latin) |
| [3] | A.I. Markushevich, "A short course on the theory of analytic functions" , Moscow (1978) (In Russian) |
Comments
References
| [a1] | K.R. Stromberg, "An introduction to classical real analysis" , Wadsworth (1981) |
How to Cite This Entry:
Euler formulas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_formulas&oldid=14630
Euler formulas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_formulas&oldid=14630
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article