Essential mapping
From Encyclopedia of Mathematics
A continuous mapping 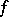 of a topological space
of a topological space 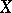 into an open simplex
into an open simplex 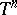 such that every continuous mapping
such that every continuous mapping 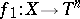 that coincides with
that coincides with 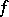 at all points of the set
at all points of the set 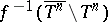 is a mapping onto the whole of
is a mapping onto the whole of 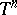 . For example, the identity mapping of
. For example, the identity mapping of 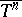 onto itself is an essential mapping.
onto itself is an essential mapping.
References
| [1] | P.S. Aleksandrov, B.A. Pasynkov, "Introduction to dimension theory" , Moscow (1973) (In Russian) |
Comments
Essential mappings are used to characterize the covering dimension (see Dimension) of normal spaces. A normal space has covering dimension 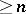 if and only if it admits an essential mapping onto the
if and only if it admits an essential mapping onto the  -dimensional simplex
-dimensional simplex 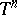 .
.
References
| [a1] | R. Engelking, "Dimension theory" , North-Holland & PWN (1978) |
How to Cite This Entry:
Essential mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Essential_mapping&oldid=12470
Essential mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Essential_mapping&oldid=12470
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article