Difference between revisions of "Epicycloid"
(Importing text file) |
m (link) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
A planar curve given by the trajectory of a point on a circle rolling on the exterior side of another circle. The parametric equations are: | A planar curve given by the trajectory of a point on a circle rolling on the exterior side of another circle. The parametric equations are: | ||
| − | + | $$x=(r+R)\cos\theta-r\cos\left[(r+R)\frac\theta r\right],$$ | |
| − | + | $$y=(r+R)\sin\theta-r\sin\left[(r+R)\frac\theta r\right],$$ | |
| − | where | + | where $r$ is the radius of the rolling and $R$ that of the fixed circle, and $\theta$ is the angle between the radius vector of the point of contact of the circles (see Fig. a, Fig. b) and the $x$-axis. |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e035860a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e035860a.gif" /> | ||
| Line 11: | Line 12: | ||
Figure: e035860a | Figure: e035860a | ||
| − | + | $m=3$ | |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e035860b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e035860b.gif" /> | ||
| Line 17: | Line 18: | ||
Figure: e035860b | Figure: e035860b | ||
| − | + | $m=3/2$ | |
| − | Depending on the value of the modulus | + | Depending on the value of the modulus $m=R/r$, the resulting epicycloid has different forms. For $m=1$ it is a [[cardioid]], and if $m$ is an integer, the curve consists of $m$ distinct branches. The cusps $A_1,\ldots,A_m$ have the polar coordinates $\rho=R$, $\phi=\pi2k/m$, $k=0,\ldots,m-1$. The vertices $B_1,\ldots,B_m$ of the curve have the coordinates $\rho=R+2r$, $\phi=\pi(2k+1)/m$. When $m$ is a rational fraction, the branches intersect each other in the interior; when $m$ is irrational there are infinitely many branches and the curve does not return to a point $M$ describing a position obtained previously; for rational $m$ the epicycloid is a closed algebraic curve. The arc length from the point $A_1$ is: |
| − | + | $$s=8Rm(1+m)\sin^2\frac\theta4,$$ | |
| − | and from | + | and from $B_1$ it is |
| − | + | $$s=4Rm(1+m)\cos\frac\theta2.$$ | |
The area of a sector bounded by two radius vectors of the curve and its arc is | The area of a sector bounded by two radius vectors of the curve and its arc is | ||
| − | + | $$S=m\pi(R+mR)(R+2mR).$$ | |
The radius of curvature is | The radius of curvature is | ||
| − | + | $$r_k=\frac{4Rm(1+m)}{2m+1}\sin\frac\theta2.$$ | |
| − | When the point is not situated on the rolling circle, but lies in its exterior (or interior) region, then the curve is called an elongated (respectively, shortened) epicycloid or | + | When the point is not situated on the rolling circle, but lies in its exterior (or interior) region, then the curve is called an elongated (respectively, shortened) epicycloid or [[epitrochoid]]. Epicycloids belong to the so-called [[cycloidal curve]]s. |
====References==== | ====References==== | ||
| Line 43: | Line 44: | ||
====Comments==== | ====Comments==== | ||
| − | Epicycloids | + | Epicycloids and [[hypocycloid]]s have many equivalent definitions. See, e.g., [[#References|[a3]]], pp. 273-277. Epicycloids and, more generally, trochoids are important for kinematical constructions, cf. [[#References|[a1]]]. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.-R. Müller, "Kinematik" , de Gruyter (1963)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> K. Strubecker, "Differential geometry" , '''I''' , de Gruyter (1964)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Berger, "Geometry" , '''I''' , Springer (1977)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> H.-R. Müller, "Kinematik" , de Gruyter (1963)</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> K. Strubecker, "Differential geometry" , '''I''' , de Gruyter (1964)</TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Berger, "Geometry" , '''I''' , Springer (1977)</TD></TR> | ||
| + | <TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French)</TD></TR> | ||
| + | </table> | ||
Latest revision as of 21:16, 12 December 2017
A planar curve given by the trajectory of a point on a circle rolling on the exterior side of another circle. The parametric equations are:
$$x=(r+R)\cos\theta-r\cos\left[(r+R)\frac\theta r\right],$$
$$y=(r+R)\sin\theta-r\sin\left[(r+R)\frac\theta r\right],$$
where $r$ is the radius of the rolling and $R$ that of the fixed circle, and $\theta$ is the angle between the radius vector of the point of contact of the circles (see Fig. a, Fig. b) and the $x$-axis.
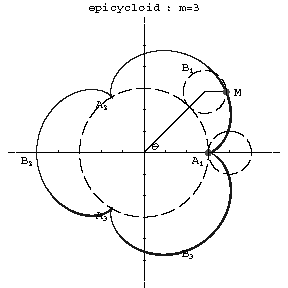
Figure: e035860a
$m=3$

Figure: e035860b
$m=3/2$
Depending on the value of the modulus $m=R/r$, the resulting epicycloid has different forms. For $m=1$ it is a cardioid, and if $m$ is an integer, the curve consists of $m$ distinct branches. The cusps $A_1,\ldots,A_m$ have the polar coordinates $\rho=R$, $\phi=\pi2k/m$, $k=0,\ldots,m-1$. The vertices $B_1,\ldots,B_m$ of the curve have the coordinates $\rho=R+2r$, $\phi=\pi(2k+1)/m$. When $m$ is a rational fraction, the branches intersect each other in the interior; when $m$ is irrational there are infinitely many branches and the curve does not return to a point $M$ describing a position obtained previously; for rational $m$ the epicycloid is a closed algebraic curve. The arc length from the point $A_1$ is:
$$s=8Rm(1+m)\sin^2\frac\theta4,$$
and from $B_1$ it is
$$s=4Rm(1+m)\cos\frac\theta2.$$
The area of a sector bounded by two radius vectors of the curve and its arc is
$$S=m\pi(R+mR)(R+2mR).$$
The radius of curvature is
$$r_k=\frac{4Rm(1+m)}{2m+1}\sin\frac\theta2.$$
When the point is not situated on the rolling circle, but lies in its exterior (or interior) region, then the curve is called an elongated (respectively, shortened) epicycloid or epitrochoid. Epicycloids belong to the so-called cycloidal curves.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
Epicycloids and hypocycloids have many equivalent definitions. See, e.g., [a3], pp. 273-277. Epicycloids and, more generally, trochoids are important for kinematical constructions, cf. [a1].
References
| [a1] | H.-R. Müller, "Kinematik" , de Gruyter (1963) |
| [a2] | K. Strubecker, "Differential geometry" , I , de Gruyter (1964) |
| [a3] | M. Berger, "Geometry" , I , Springer (1977) |
| [a4] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
Epicycloid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Epicycloid&oldid=13845