Endomorphism

of an algebraic system

A mapping of an algebraic system into itself that is compatible with its structure. Namely, if is an algebraic system with a signature consisting of a set of operation symbols and a set of predicate symbols, then an endomorphism must satisfy the following conditions:

1) for any -ary operation and any sequence of elements of ;

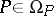2) for any -place predicate and any sequence of elements of .

The concept of an endomorphism is a special case of that of a homomorphism of two algebraic systems. The endomorphisms of any algebraic system form a monoid under the operation of composition of mappings, whose unit element is the identity mapping of the underlying set of the system (cf. Endomorphism semi-group).

An endomorphism having an inverse is called an automorphism of the algebraic system.

Comments

Thus, by way of one of the simplest examples, an endomorphism of an Abelian group is a mapping such that , for all elements and in and for all 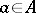. For an endomorphism of a ring with a unit 1, the requirements are that 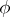be an endomorphism of the underlying commutative group and that, moreover, and for all .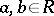

References

[a1]	P.M. Cohn, "Universal algebra" , Reidel (1981)