Difference between revisions of "E-M-factorization-system-in-a-category"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 116 formulas out of 127 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 127 formulas, 116 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | The simple fact that every function $f : A \rightarrow B$ between sets can be factored through its image (i.e., written as a composite | ||
| − | + | \begin{equation*} A \stackrel { f } { \rightarrow } B = A \stackrel { e } { \rightarrow } f [ A ] \stackrel { m } { \rightarrow } B, \end{equation*} | |
| − | + | where $e : A \rightarrow f [ A ]$ is the codomain-restriction of $f$ and $m : f [ A ] \rightarrow B$ is the inclusion) is abstracted in [[Category|category]] theory to an axiomatic theory of factorization structures $( E , M )$ for morphisms of a category $\frak A$. Here, $E$ and $M$ are classes of $\frak A$-morphisms (the requirements $E \subseteq \operatorname { Epi } ( \mathfrak { A } )$ and $M \subseteq \text { Mono } ( \mathfrak { A } )$ were originally included, but later dropped) such that each $\frak A$-morphism has an $( E , M )$-factorization | |
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e120/e120010/e12001016.png"/></td> </tr></table> | ||
| + | |||
| + | Clearly, further assumptions on $E$ and $M$ are required to make the factorization theory useful. A careful analysis has revealed that the crucial requirement that causes $( E , M )$-factorizations to have appropriate characteristics is the so-called "unique E,M-diagonalization" condition, described in 3) below. Such factorization structures for morphisms have turned out to be especially useful for "well-behaved" categories (e.g., those having products and satisfying suitable smallness conditions). Morphism factorizations have been transformed into powerful categorical tools by successive generalizations to | ||
a) factorization structures for sources in a category; | a) factorization structures for sources in a category; | ||
| Line 17: | Line 25: | ||
d) factorization structures for structured flows with respect to a functor. The simplest of these is described first and in most detail. A general reference for this area is [[#References|[a1]]], Chaps. IV; V. | d) factorization structures for structured flows with respect to a functor. The simplest of these is described first and in most detail. A general reference for this area is [[#References|[a1]]], Chaps. IV; V. | ||
| − | Let | + | Let $E$ and $M$ be classes of morphisms in a category $\frak A$ (cf. also [[Morphism|Morphism]]). Then $( E , M )$ is called a factorization structure for morphisms in $\frak A$, and $\frak A$ is called $( E , M )$-structured, provided that |
| − | 1) each of | + | 1) each of $E$ and $M$ is closed under composition with isomorphisms; |
| − | 2) | + | 2) $\frak A$ has $( E , M )$-factorizations (of morphisms); i.e., each morphism $f$ in $\frak A$ has a factorization $f = m \circ e$, with $e \in E$ and $m \in M$; and |
| − | 3) | + | 3) $\frak A$ has the unique $( E , M )$-diagonalization property; i.e., for each commutative square |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e120/e120010/e12001041.png"/></td> </tr></table> |
| − | with | + | with $e \in E$ and $m \in M$, there exists a unique diagonal, i.e., a morphism $d$ such that $d \circ e = f$ and $m \circ d = g$. For example, the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e120/e120010/e12001047.png"/> of sets and functions has exactly four different factorization structures for morphisms, the most frequently used of which is $( \text { Epi } , \text { Mono } ) =$ (surjections, injections) described above, whereas the category $\mathbf{Top}$ of topological spaces and continuous functions has more than a proper class of different factorization structures for morphisms (see [[#References|[a6]]]), but <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e120/e120010/e12001050.png"/> is not one of them (since it does not satisfy the diagonalization condition). |
| − | Diagonalization is crucial in that it guarantees essential uniqueness of factorizations. Also, it can be shown that each of | + | Diagonalization is crucial in that it guarantees essential uniqueness of factorizations. Also, it can be shown that each of $E$ and $M$ determines the other via the diagonal property, that $E$ and $M$ are compositive, and that $E \cap M = \operatorname{Iso}$. Many other pleasant properties of $E$ and $M$ follow from the definition above. $E$ and $M$ are dual to each other, $M$ is well-behaved with respect to limits and $E$ is well-behaved with respect to co-limits. Also, there exist satisfactory external characterizations of classes $E$ in a category that guarantee the existence of a class $M$ such that $( E , M )$ will be a factorization system for morphisms (see, e.g., [[#References|[a2]]]). Many familiar categories have particular morphism factorization structures. Every finitely-complete category that has intersections is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e120/e120010/e12001065.png"/>-structured. Each category that has equalizers and intersections is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e120/e120010/e12001066.png"/>-structured, and a category that has pullbacks and co-equalizers is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e120/e120010/e12001067.png"/>-structured if and only if regular epimorphisms in it are compositive. |
| − | Factorization structures for sources (i.e., families of morphisms with a common domain) in a category | + | Factorization structures for sources (i.e., families of morphisms with a common domain) in a category $\frak A$ are defined quite analogously to those for single morphisms. Here, one has a class $E$ of morphisms and a family $\mathfrak{M}$ of sources, each closed under composition with isomorphisms, such that each source $\mathcal{S}$ in $\frak A$ has a factorization $\mathcal{S} = \mathcal{M} \circ e$ with $e \in E$ and $\mathcal{M} \in \mathfrak { M }$, and each commuting square in $\frak A$, with sources as right side and bottom side, a member of $E$ as top side and a member of $\mathfrak{M}$ as bottom side, has a diagonalization. A category that has these properties is called an $( E , \mathfrak { M } )$-category. Notice that now $E$ and $\mathfrak{M}$ are no longer dual. The dual theory is that of a factorization structure for sinks, i.e., an $( \mathfrak { E } , M )$-category. Interestingly, in any $( E , \mathfrak { M } )$-category, $E$ must be contained in the class of all epimorphisms. (As a consequence, uniqueness of the diagonal comes without hypothesizing it.) However, $\mathfrak{M}$ is contained in the family of all mono-sources if and only if $\mathbf{A}$ has co-equalizers and $E$ contains all regular epimorphisms. There exist reasonable external characterizations of classes $E$ in a category that guarantee the existence of a family $\mathfrak{M}$ such that $\frak A$ is an $( E , \mathfrak { M } )$-category (see e.g., [[#References|[a1]]], 15.14) and a reasonable theory exists for extending factorization structures for morphisms to those for sources (respectively, sinks). |
Factorization structures with respect to functors provide yet a further generalization, as follows. | Factorization structures with respect to functors provide yet a further generalization, as follows. | ||
| − | Let | + | Let $G : \mathfrak { A } \rightarrow \mathfrak { X }$ be a [[Functor|functor]], let $E$ be a class of $G$-structured arrows, and let $\mathfrak{M}$ be a conglomerate of $\frak A$-sources. $( E , \mathfrak { M } )$ is called a factorization structure for $G$, and $G$ is called an $( E , \mathfrak { M } )$-functor provided that: |
| − | A) | + | A) $E$ and $\mathfrak{M}$ are closed under composition with isomorphisms; |
| − | B) | + | B) $G$ has $( E , \mathfrak { M } )$-factorizations, i.e., for each $G$-structured source $( f _ { i } : X \rightarrow G A _ { i } ) _ { I }$ there exist |
| − | + | \begin{equation*} e : X \rightarrow G A \in E \text { and } \mathcal{M} = ( m _ { i } : A \rightarrow A _ { i } ) _ { I } \in \mathfrak { M } \end{equation*} | |
such that | such that | ||
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e120/e120010/e120010112.png"/></td> </tr></table> |
| − | C) | + | C) $G$ has the unique $( E , \mathfrak { M } )$-diagonalization property, i.e., whenever $f : X \rightarrow G A$ and $e : X \rightarrow G B$ are $G$-structured arrows with $( e , B ) \in E$, and $\mathcal{M} = ( m _ { i } : A \rightarrow A _ { i } ) _ { I }$ and $\mathcal{S} = ( f _ { i } : B \rightarrow A _ { i } ) _ { I }$ are $\frak A$-sources with $\mathcal{M} \in \mathfrak { M }$, such that $( G m _ { i } ) \circ f = ( G f _ { i } ) \circ e$ for each $i \in I$, then there exists a unique diagonal, i.e., an $\frak A$-morphism $d : B \rightarrow A$ with $f = G d \circ e$ and ${\cal S = M} \circ d$. |
| − | Interestingly, this precisely captures the important categorical notion of adjointness: i.e., a functor is an adjoint functor if and only if it is an | + | Interestingly, this precisely captures the important categorical notion of adjointness: i.e., a functor is an adjoint functor if and only if it is an $( E , \mathfrak { M } )$-functor for some $E$ and $\mathfrak{M}$. |
Generalizations of factorization theory to flows and flows with respect to a functor can be found in [[#References|[a5]]] and [[#References|[a11]]], respectively. | Generalizations of factorization theory to flows and flows with respect to a functor can be found in [[#References|[a5]]] and [[#References|[a11]]], respectively. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> J. Adamek, H. Herrlich, G.E. Strecker, "Abstract and concrete categories" , Wiley–Interscience (1990)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> A.K. Bousfield, "Constructions of factorization systems in categories" ''J. Pure Appl. Algebra'' , '''9''' (1977) pp. 207–220</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> C. Cassidy, M. Hébert, G.M. Kelly, "Reflective subcategories, localizations and factorization systems" ''J. Austral. Math. Soc.'' , '''38''' (1985) pp. 287–329 (Corrigenda: 41 (1986), 286)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> P.J. Freyd, G.M. Kelly, "Categories of continuous functors I" ''J. Pure Appl. Algebra'' , '''2''' (1972) pp. 169–191</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> H. Herrlich, W. Meyer, "Factorization of flows and completeness of categories" ''Quaest. Math.'' , '''17''' : 1 (1994) pp. 1–11</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> H. Herrlich, G. Salicrup, R. Vazquez, "Dispersed factorization structures" ''Canad. J. Math.'' , '''31''' (1979) pp. 1059–1071</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> H. Herrlich, G.E. Strecker, "Semi-universal maps and universal initial completions" ''Pacific J. Math.'' , '''82''' (1979) pp. 407–428</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> R.-E. Hoffmann, "Factorization of cones" ''Math. Nachr.'' , '''87''' (1979) pp. 221–238</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> R. Nakagawa, "A note on $( E , M )$-functors" H. Herrlich (ed.) G. Preuss (ed.) , ''Categorical Topology'' , ''Lecture Notes Math.'' , '''719''' , Springer (1979) pp. 250–258</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> G.E. Strecker, "Perfect sources" A. Dold (ed.) B. Eckmann (ed.) , ''Categorical Topol. Proc. Conf. Mannheim 1975'' , ''Lecture Notes Math.'' , '''540''' , Springer (1976) pp. 605–624</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> G.E. Strecker, "Flows with respect to a functor" ''Appl. Categorical Struct.'' (to appear)</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> W. Tholen, "Factorizations of cones along a functor" ''Quaest. Math.'' , '''2''' (1977) pp. 335–353</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> W. Tholen, "Factorizations, localizations, and the orthogonal subcategory problem" ''Math. Nachr.'' , '''114''' (1983) pp. 63–85</td></tr></table> |
Revision as of 16:58, 1 July 2020
The simple fact that every function $f : A \rightarrow B$ between sets can be factored through its image (i.e., written as a composite
\begin{equation*} A \stackrel { f } { \rightarrow } B = A \stackrel { e } { \rightarrow } f [ A ] \stackrel { m } { \rightarrow } B, \end{equation*}
where $e : A \rightarrow f [ A ]$ is the codomain-restriction of $f$ and $m : f [ A ] \rightarrow B$ is the inclusion) is abstracted in category theory to an axiomatic theory of factorization structures $( E , M )$ for morphisms of a category $\frak A$. Here, $E$ and $M$ are classes of $\frak A$-morphisms (the requirements $E \subseteq \operatorname { Epi } ( \mathfrak { A } )$ and $M \subseteq \text { Mono } ( \mathfrak { A } )$ were originally included, but later dropped) such that each $\frak A$-morphism has an $( E , M )$-factorization
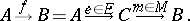 |
Clearly, further assumptions on $E$ and $M$ are required to make the factorization theory useful. A careful analysis has revealed that the crucial requirement that causes $( E , M )$-factorizations to have appropriate characteristics is the so-called "unique E,M-diagonalization" condition, described in 3) below. Such factorization structures for morphisms have turned out to be especially useful for "well-behaved" categories (e.g., those having products and satisfying suitable smallness conditions). Morphism factorizations have been transformed into powerful categorical tools by successive generalizations to
a) factorization structures for sources in a category;
b) factorization structures for structured sources with respect to a functor;
c) factorization structures for flows in a category; and
d) factorization structures for structured flows with respect to a functor. The simplest of these is described first and in most detail. A general reference for this area is [a1], Chaps. IV; V.
Let $E$ and $M$ be classes of morphisms in a category $\frak A$ (cf. also Morphism). Then $( E , M )$ is called a factorization structure for morphisms in $\frak A$, and $\frak A$ is called $( E , M )$-structured, provided that
1) each of $E$ and $M$ is closed under composition with isomorphisms;
2) $\frak A$ has $( E , M )$-factorizations (of morphisms); i.e., each morphism $f$ in $\frak A$ has a factorization $f = m \circ e$, with $e \in E$ and $m \in M$; and
3) $\frak A$ has the unique $( E , M )$-diagonalization property; i.e., for each commutative square
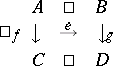 |
with $e \in E$ and $m \in M$, there exists a unique diagonal, i.e., a morphism $d$ such that $d \circ e = f$ and $m \circ d = g$. For example, the category  of sets and functions has exactly four different factorization structures for morphisms, the most frequently used of which is $( \text { Epi } , \text { Mono } ) =$ (surjections, injections) described above, whereas the category $\mathbf{Top}$ of topological spaces and continuous functions has more than a proper class of different factorization structures for morphisms (see [a6]), but
of sets and functions has exactly four different factorization structures for morphisms, the most frequently used of which is $( \text { Epi } , \text { Mono } ) =$ (surjections, injections) described above, whereas the category $\mathbf{Top}$ of topological spaces and continuous functions has more than a proper class of different factorization structures for morphisms (see [a6]), but 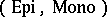 is not one of them (since it does not satisfy the diagonalization condition).
is not one of them (since it does not satisfy the diagonalization condition).
Diagonalization is crucial in that it guarantees essential uniqueness of factorizations. Also, it can be shown that each of $E$ and $M$ determines the other via the diagonal property, that $E$ and $M$ are compositive, and that $E \cap M = \operatorname{Iso}$. Many other pleasant properties of $E$ and $M$ follow from the definition above. $E$ and $M$ are dual to each other, $M$ is well-behaved with respect to limits and $E$ is well-behaved with respect to co-limits. Also, there exist satisfactory external characterizations of classes $E$ in a category that guarantee the existence of a class $M$ such that $( E , M )$ will be a factorization system for morphisms (see, e.g., [a2]). Many familiar categories have particular morphism factorization structures. Every finitely-complete category that has intersections is 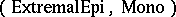 -structured. Each category that has equalizers and intersections is
-structured. Each category that has equalizers and intersections is 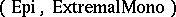 -structured, and a category that has pullbacks and co-equalizers is
-structured, and a category that has pullbacks and co-equalizers is 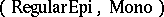 -structured if and only if regular epimorphisms in it are compositive.
-structured if and only if regular epimorphisms in it are compositive.
Factorization structures for sources (i.e., families of morphisms with a common domain) in a category $\frak A$ are defined quite analogously to those for single morphisms. Here, one has a class $E$ of morphisms and a family $\mathfrak{M}$ of sources, each closed under composition with isomorphisms, such that each source $\mathcal{S}$ in $\frak A$ has a factorization $\mathcal{S} = \mathcal{M} \circ e$ with $e \in E$ and $\mathcal{M} \in \mathfrak { M }$, and each commuting square in $\frak A$, with sources as right side and bottom side, a member of $E$ as top side and a member of $\mathfrak{M}$ as bottom side, has a diagonalization. A category that has these properties is called an $( E , \mathfrak { M } )$-category. Notice that now $E$ and $\mathfrak{M}$ are no longer dual. The dual theory is that of a factorization structure for sinks, i.e., an $( \mathfrak { E } , M )$-category. Interestingly, in any $( E , \mathfrak { M } )$-category, $E$ must be contained in the class of all epimorphisms. (As a consequence, uniqueness of the diagonal comes without hypothesizing it.) However, $\mathfrak{M}$ is contained in the family of all mono-sources if and only if $\mathbf{A}$ has co-equalizers and $E$ contains all regular epimorphisms. There exist reasonable external characterizations of classes $E$ in a category that guarantee the existence of a family $\mathfrak{M}$ such that $\frak A$ is an $( E , \mathfrak { M } )$-category (see e.g., [a1], 15.14) and a reasonable theory exists for extending factorization structures for morphisms to those for sources (respectively, sinks).
Factorization structures with respect to functors provide yet a further generalization, as follows.
Let $G : \mathfrak { A } \rightarrow \mathfrak { X }$ be a functor, let $E$ be a class of $G$-structured arrows, and let $\mathfrak{M}$ be a conglomerate of $\frak A$-sources. $( E , \mathfrak { M } )$ is called a factorization structure for $G$, and $G$ is called an $( E , \mathfrak { M } )$-functor provided that:
A) $E$ and $\mathfrak{M}$ are closed under composition with isomorphisms;
B) $G$ has $( E , \mathfrak { M } )$-factorizations, i.e., for each $G$-structured source $( f _ { i } : X \rightarrow G A _ { i } ) _ { I }$ there exist
\begin{equation*} e : X \rightarrow G A \in E \text { and } \mathcal{M} = ( m _ { i } : A \rightarrow A _ { i } ) _ { I } \in \mathfrak { M } \end{equation*}
such that
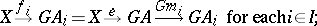 |
C) $G$ has the unique $( E , \mathfrak { M } )$-diagonalization property, i.e., whenever $f : X \rightarrow G A$ and $e : X \rightarrow G B$ are $G$-structured arrows with $( e , B ) \in E$, and $\mathcal{M} = ( m _ { i } : A \rightarrow A _ { i } ) _ { I }$ and $\mathcal{S} = ( f _ { i } : B \rightarrow A _ { i } ) _ { I }$ are $\frak A$-sources with $\mathcal{M} \in \mathfrak { M }$, such that $( G m _ { i } ) \circ f = ( G f _ { i } ) \circ e$ for each $i \in I$, then there exists a unique diagonal, i.e., an $\frak A$-morphism $d : B \rightarrow A$ with $f = G d \circ e$ and ${\cal S = M} \circ d$.
Interestingly, this precisely captures the important categorical notion of adjointness: i.e., a functor is an adjoint functor if and only if it is an $( E , \mathfrak { M } )$-functor for some $E$ and $\mathfrak{M}$.
Generalizations of factorization theory to flows and flows with respect to a functor can be found in [a5] and [a11], respectively.
References
| [a1] | J. Adamek, H. Herrlich, G.E. Strecker, "Abstract and concrete categories" , Wiley–Interscience (1990) |
| [a2] | A.K. Bousfield, "Constructions of factorization systems in categories" J. Pure Appl. Algebra , 9 (1977) pp. 207–220 |
| [a3] | C. Cassidy, M. Hébert, G.M. Kelly, "Reflective subcategories, localizations and factorization systems" J. Austral. Math. Soc. , 38 (1985) pp. 287–329 (Corrigenda: 41 (1986), 286) |
| [a4] | P.J. Freyd, G.M. Kelly, "Categories of continuous functors I" J. Pure Appl. Algebra , 2 (1972) pp. 169–191 |
| [a5] | H. Herrlich, W. Meyer, "Factorization of flows and completeness of categories" Quaest. Math. , 17 : 1 (1994) pp. 1–11 |
| [a6] | H. Herrlich, G. Salicrup, R. Vazquez, "Dispersed factorization structures" Canad. J. Math. , 31 (1979) pp. 1059–1071 |
| [a7] | H. Herrlich, G.E. Strecker, "Semi-universal maps and universal initial completions" Pacific J. Math. , 82 (1979) pp. 407–428 |
| [a8] | R.-E. Hoffmann, "Factorization of cones" Math. Nachr. , 87 (1979) pp. 221–238 |
| [a9] | R. Nakagawa, "A note on $( E , M )$-functors" H. Herrlich (ed.) G. Preuss (ed.) , Categorical Topology , Lecture Notes Math. , 719 , Springer (1979) pp. 250–258 |
| [a10] | G.E. Strecker, "Perfect sources" A. Dold (ed.) B. Eckmann (ed.) , Categorical Topol. Proc. Conf. Mannheim 1975 , Lecture Notes Math. , 540 , Springer (1976) pp. 605–624 |
| [a11] | G.E. Strecker, "Flows with respect to a functor" Appl. Categorical Struct. (to appear) |
| [a12] | W. Tholen, "Factorizations of cones along a functor" Quaest. Math. , 2 (1977) pp. 335–353 |
| [a13] | W. Tholen, "Factorizations, localizations, and the orthogonal subcategory problem" Math. Nachr. , 114 (1983) pp. 63–85 |
E-M-factorization-system-in-a-category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=E-M-factorization-system-in-a-category&oldid=15835