Dunford-Pettis property
The property of a Banach space 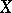 that every continuous operator
that every continuous operator 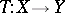 sending bounded sets of
sending bounded sets of  into relatively weakly compact sets of
into relatively weakly compact sets of 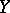 (called weakly compact operators) also transforms weakly compact sets of
(called weakly compact operators) also transforms weakly compact sets of 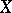 into norm-compact sets of
into norm-compact sets of 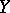 (such operators are called completely continuous; cf. also Completely-continuous operator). In short, it requires that weakly compact operators on
(such operators are called completely continuous; cf. also Completely-continuous operator). In short, it requires that weakly compact operators on 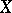 are completely continuous.
are completely continuous.
Equivalently, given weakly convergent sequences 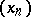 in
in 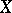 and
and 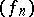 in its topological dual
in its topological dual 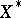 , the sequence
, the sequence 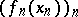 also converges. Contrary to intuition this does not always happen. For example, if
also converges. Contrary to intuition this does not always happen. For example, if 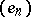 denotes the canonical basis of
denotes the canonical basis of 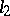 , then
, then 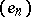 is weakly convergent to zero although
is weakly convergent to zero although 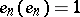 .
.
The property was isolated and defined by A. Grothendieck [a7] after the following classical result of N. Dunford and B.J. Pettis [a5]: For any measure 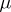 and any Banach space
and any Banach space 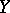 , every weakly compact operator
, every weakly compact operator 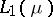 into
into  is completely continuous.
is completely continuous.
This result has its roots in examples of Sirvint, S. Kakutani, Y. Mimura and K. Yosida concerning weakly compact non-compact operators on 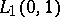 which could be proven to have a compact square. The main examples of spaces having the Dunford–Pettis property are the spaces
which could be proven to have a compact square. The main examples of spaces having the Dunford–Pettis property are the spaces 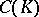 of continuous functions on a compact space and the spaces
of continuous functions on a compact space and the spaces 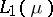 of integrable functions on a measure space, as well as complemented subspaces of these spaces. Other classical function spaces having the Dunford–Pettis property are: the Hardy space
of integrable functions on a measure space, as well as complemented subspaces of these spaces. Other classical function spaces having the Dunford–Pettis property are: the Hardy space 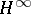 and its higher duals (cf. also Hardy spaces); the quotient space
and its higher duals (cf. also Hardy spaces); the quotient space 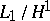 and its higher duals (the space
and its higher duals (the space 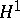 itself does not have the Dunford–Pettis property, nor does its dual BMO or its pre-dual VMO) (cf. also
itself does not have the Dunford–Pettis property, nor does its dual BMO or its pre-dual VMO) (cf. also 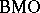 -space;
-space; 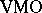 -space); the ball algebra, the poly-disc algebra and their duals, and the spaces
-space); the ball algebra, the poly-disc algebra and their duals, and the spaces 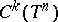 of
of 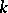 -smooth functions on the
-smooth functions on the  -dimensional torus.
-dimensional torus.
A classical survey on the topic is [a4]. Many of the open problems stated there have been solved by now, mainly by J. Bourgain [a2], [a3], who introduced new techniques for working with the Dunford–Pettis property, and by M. Talagrand [a8], who gave an example of a space 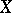 with the Dunford–Pettis property such that
with the Dunford–Pettis property such that  and
and 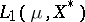 fail the Dunford–Pettis property.
fail the Dunford–Pettis property.
The Dunford–Pettis property is not easy to work with, nor is it well understood. In general, it is difficult to prove that a given concrete space has the property; quoting J. Diestel: "I know of no case where the reward (when it comes) is easily attained" . On the question of structure theorems, many open problems remain. One of the most striking is as follows. When does the dual of a space that has the Dunford–Pettis property have the Dunford–Pettis property? It is clear that if 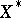 has the Dunford–Pettis property, then so does
has the Dunford–Pettis property, then so does 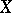 . From Rosenthal's
. From Rosenthal's 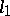 theorem it follows that if
theorem it follows that if 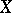 has the Dunford–Pettis property and does not contain
has the Dunford–Pettis property and does not contain 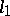 , then
, then  has the Dunford–Pettis property. Stegall has shown that although the space
has the Dunford–Pettis property. Stegall has shown that although the space 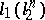 has the Dunford–Pettis property (since weakly convergent sequences are norm convergent), its dual
has the Dunford–Pettis property (since weakly convergent sequences are norm convergent), its dual 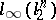 does not have the Dunford–Pettis property (because it contains complemented copies of
does not have the Dunford–Pettis property (because it contains complemented copies of 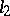 ).
).
A reflexive space does not have the Dunford–Pettis property unless it is finite-dimensional. The Grothendieck spaces 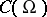 ,
, 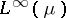 ,
, 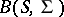 , and
, and 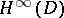 (cf. Grothendieck space) also possess the Dunford–Pettis property (see [a9], [a10]).
(cf. Grothendieck space) also possess the Dunford–Pettis property (see [a9], [a10]).
A Banach space 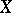 is a Grothendieck space with the Dunford–Pettis property if and only if every weak-
is a Grothendieck space with the Dunford–Pettis property if and only if every weak- convergent sequence in
convergent sequence in 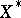 converges weakly and uniformly on weakly compact subsets of
converges weakly and uniformly on weakly compact subsets of 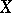 , if and only if every bounded linear operator from
, if and only if every bounded linear operator from 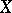 into
into 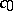 is weakly compact and maps weakly compact sets into norm-compact sets.
is weakly compact and maps weakly compact sets into norm-compact sets.
An interesting phenomenon about Grothendieck spaces with the Dunford–Pettis property is that in many cases strong convergence of operators on such a space (cf. also Strong topology) implies uniform convergence. For example, let  be a Grothendieck space with the Dunford–Pettis property. Then:
be a Grothendieck space with the Dunford–Pettis property. Then:
1) 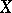 does not have a Schauder decomposition, or equivalently, if a sequence of projections
does not have a Schauder decomposition, or equivalently, if a sequence of projections 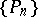 on
on 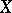 converges weakly to the identity operator
converges weakly to the identity operator 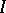 , then
, then 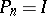 for
for  sufficiently large;
sufficiently large;
2) if the Cesáro mean 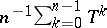 of an operator
of an operator 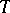 on
on 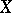 converges strongly, then it converges uniformly;
converges strongly, then it converges uniformly;
3) all 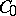 -semi-groups on
-semi-groups on 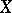 are norm-continuous (see [a9], [a10]);
are norm-continuous (see [a9], [a10]);
4) all strongly continuous cosine operator functions on 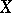 are norm-continuous [a11];
are norm-continuous [a11];
5) for general ergodic systems on 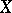 , in particular,
, in particular, 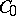 -semi-groups and cosine operator functions, strong ergodicity implies uniform ergodicity (see [a12]).
-semi-groups and cosine operator functions, strong ergodicity implies uniform ergodicity (see [a12]).
References
| [a1] | J. Bourgain, "On the Dunford–Pettis property" Proc. Amer. Math. Soc. , 81 (1981) pp. 265–272 |
| [a2] | J. Bourgain, "New Banach space properties of the disc algebra and 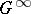 " Acta Math. , 152 (1984) pp. 1–48 " Acta Math. , 152 (1984) pp. 1–48 |
| [a3] | J. Bourgain, "The Dunford–Pettis property for the ball-algebras, the polydisc algebra, and the Sobolev spaces" Studia Math. , 77 (1984) pp. 245–253 |
| [a4] | J. Diestel, "A survey or results related to the Dunford–Pettis property" , Contemp. Math. , 2 , Amer. Math. Soc. (1980) pp. 15–60 |
| [a5] | N. Dunford, B.J. Pettis, "Linear operations on summable functions" Trans. Amer. Math. Soc. , 47 (1940) pp. 323–392 |
| [a6] | N. Dunford, J.T. Schwartz, "Linear operators" , I. General theory , Wiley, reprint (1988) |
| [a7] | A. Grothendieck, "Sur les applications linéaires faiblement compactes d'espaces de type  " Canad. J. Math. , 5 (1953) pp. 129–173 " Canad. J. Math. , 5 (1953) pp. 129–173 |
| [a8] | M. Talagrand, "La propriété de Dunford–Pettis dans 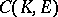 et et 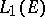 " Israel J. Math. , 44 (1983) pp. 317–321 " Israel J. Math. , 44 (1983) pp. 317–321 |
| [a9] | H.P. Lotz, "Tauberian theorems for operators on 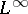 and similar spaces" , Functional Analysis III. Surveys and Recent Results , North-Holland (1984) and similar spaces" , Functional Analysis III. Surveys and Recent Results , North-Holland (1984) |
| [a10] | H.P. Lotz, "Uniform convergence of operators on 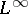 and similar spaces" Math. Z. , 190 (1985) pp. 207–220 and similar spaces" Math. Z. , 190 (1985) pp. 207–220 |
| [a11] | S.-Y. Shaw, "Asymptotic behavior of pseudoresolvents on some Grothendieck spaces" Publ. RIMS Kyoto Univ. , 24 (1988) pp. 277–282 |
| [a12] | S.-Y. Shaw, "Uniform convergence of ergodic limits and approximate solutions" Proc. Amer. Math. Soc. , 114 (1992) pp. 405–411 |
Dunford-Pettis property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dunford-Pettis_property&oldid=22367