Difference between revisions of "Divisor problems"
m (link) |
Ulf Rehmann (talk | contribs) m (tex done) |
||
| Line 1: | Line 1: | ||
| − | {{TEX| | + | {{TEX|done}} |
Problems in number theory concerned with the asymptotic behaviour of the summation functions | Problems in number theory concerned with the asymptotic behaviour of the summation functions | ||
| Line 44: | Line 44: | ||
This is the problem of the best asymptotic expression for the sum | This is the problem of the best asymptotic expression for the sum | ||
| − | + | $$ | |
| + | \sum _ {n \leq x} \tau _{k} (n) \ = \ D _{k} (x) , | ||
| + | $$ | ||
| + | |||
| + | |||
| + | as $ x \rightarrow \infty $; | ||
| + | in particular, if $ k = 2 $, | ||
| + | |||
| + | |||
| + | $$ | ||
| + | \tau _{2} (n) \ = \ \tau (n) ,\ \ | ||
| + | D _{2} (x) \ = \ D (x) . | ||
| + | $$ | ||
| + | |||
| + | |||
| + | The generalized divisor problem is closely connected with the behaviour of the Riemann [[Zeta-function|zeta-function]] $ \zeta (s) $ | ||
| + | in the critical strip of values of $ s $. | ||
| + | In fact, the following formula is valid for non-integer $ x > 0 $, | ||
| + | $ c > 1 $: | ||
| + | |||
| − | + | $$ | |
| + | D _{k} (x) \ = \ | ||
| + | \frac{1}{2 \pi i} | ||
| − | + | \int\limits _ {c - i \infty} ^ {c + i \infty} \zeta ^{k} (s) | |
| + | \frac{x ^ s}{s} | ||
| + | \ ds . | ||
| + | $$ | ||
| − | |||
| − | + | Here, the integrand has at the point $ s = 1 $ | |
| + | a pole of order $ k $ | ||
| + | with residue of the form $ xP _{k} ( \mathop{\rm ln}\nolimits \ x ) $ | ||
| + | where $ P _{k} $ | ||
| + | is a polynomial of degree $ k - 1 $. | ||
| − | |||
Let | Let | ||
| − | + | $$ | |
| + | D _{k} (x) \ = \ x P _{k} ( \mathop{\rm ln}\nolimits \ x ) + \Delta _{k} (x) | ||
| + | $$ | ||
| − | |||
| − | < | + | and let $ \gamma _{k} < \gamma < 1 $, |
| + | where $ \gamma _{k} $ | ||
| + | is the greatest lower bound of the numbers $ \sigma $ | ||
| + | for which | ||
| + | |||
| + | $$ | ||
| + | \int\limits _ {- \infty} ^ \infty | ||
| + | \frac{| \zeta ( \sigma + i t ) | ^ 2k}{| \sigma + i t | ^ 2} | ||
| + | \ dt \ < \ \infty . | ||
| + | $$ | ||
| + | |||
The following formulas are then valid: | The following formulas are then valid: | ||
| − | + | $$ | |
| + | \Delta _{k} (x) \ = \ | ||
| + | \frac{1}{2 \pi i} | ||
| + | |||
| + | \lim _ {T \rightarrow \infty} \ \int\limits _ {\gamma - i T} ^ {\gamma + i T} | ||
| + | \zeta ^{k} (s) | ||
| + | \frac{x ^ s}{s} | ||
| + | \ ds ; | ||
| + | $$ | ||
| + | |||
and the inverse Mellin formula | and the inverse Mellin formula | ||
| − | + | $$ | |
| + | |||
| + | \frac{\zeta ^{k} (s)}{s} | ||
| + | \ = \ \int\limits _{0} ^ \infty | ||
| + | \Delta _{k} (x) x ^{-s-1} \ dx ,\ \ s = \sigma + i t , | ||
| + | $$ | ||
| + | |||
| + | |||
| + | where the integral exists in the mean-square sense for $ \gamma _{k} < \sigma < 1 $. | ||
| − | |||
| − | Estimates of the rest term | + | Estimates of the rest term $ \Delta _{k} (x) $ |
| + | in the formula for $ D _{k} (x) $ | ||
| + | are still (1988) far from what might be expected. Let $ \alpha _{k} $ | ||
| + | be the smallest of the numbers $ \alpha $ | ||
| + | for which | ||
| − | + | $$ | |
| + | \Delta _{k} (x) \ \ll \ x ^ {\alpha + \epsilon} | ||
| + | $$ | ||
| − | |||
| − | + | for any $ \epsilon > 0 $. | |
| + | The following estimates are known: | ||
| − | + | $$ | |
| + | \alpha _{k} \ \leq \ | ||
| + | \frac{k - 1}{k + 1} | ||
| + | , | ||
| + | $$ | ||
| − | |||
| − | + | $$ | |
| + | \alpha _{k} \ \leq \ | ||
| + | \frac{k - 1}{k + 2} | ||
| + | \ \ {\textrm{ for }} \ k \geq 4 . | ||
| + | $$ | ||
| − | |||
| − | + | These estimates can be rendered more precise for individual values of $ k $: | |
| − | |||
| − | + | $$ | |
| + | \alpha _{3} \ \leq \ | ||
| + | \frac{37}{75} | ||
| + | ,\ \ \alpha _{7} \ \leq \ | ||
| + | \frac{71}{107} | ||
| + | ,\ \ | ||
| + | \alpha _{8} \ \leq \ | ||
| + | \frac{41}{59} | ||
| + | ,\ \ \alpha _{9} \ \leq \ | ||
| + | \frac{26}{35} | ||
| + | ,\ \ | ||
| + | \alpha _{11} \ \leq \ | ||
| + | \frac{19}{25} | ||
| + | . | ||
| + | $$ | ||
| + | |||
| + | |||
| + | The last result giving an estimate from above for $ \alpha _{k} $ | ||
| + | was obtained in [[#References|[3]]] by developing the idea of the [[Vinogradov method|Vinogradov method]]: There is an absolute constant $ c > 0 $ | ||
| + | such that | ||
| + | |||
| + | $$ | ||
| + | \alpha _{k} \ \leq \ 1 - | ||
| + | \frac{c}{k ^ 2/3} | ||
| + | ,\ \ | ||
| + | k = 2 ,\ 3 ,\dots . | ||
| + | $$ | ||
| + | |||
| + | |||
| + | This estimate follows from an estimate of $ \zeta (s) $ | ||
| + | in the critical strip: For $ 1 / 2 \leq \sigma \leq 1 $, | ||
| + | $ | t | \geq 2 $ | ||
| + | there is a constant $ a > 1 $ | ||
| + | such that | ||
| + | |||
| + | $$ | ||
| + | \zeta ( \sigma + i t ) \ \ll \ | t | ^ {a ( 1 - \sigma ) ^ 3/2} \mathop{\rm ln}\nolimits \ | t | . | ||
| + | $$ | ||
| + | |||
On the other hand, it was shown by Hardy that | On the other hand, it was shown by Hardy that | ||
| − | + | $$ | |
| + | \alpha _{k} \ \geq \ | ||
| + | \frac{k - 1}{2k} | ||
| + | . | ||
| + | $$ | ||
| + | |||
| + | |||
| + | Regarding the value of $ \Delta _{k} (x) $, | ||
| + | there is the hypothesis that | ||
| + | |||
| + | $$ | ||
| + | \alpha _{k} \ = \ | ||
| + | \frac{k - 1}{2k} | ||
| − | + | $$ | |
| − | |||
| − | for all | + | for all $ k \geq 2 $. |
| + | However, it cannot be justified, even not by solving the [[Lindelöf hypothesis|Lindelöf hypothesis]]: | ||
| − | + | $$ | |
| + | \zeta ( \sigma + i t ) \ \ll \ | t | ^ \epsilon $$ | ||
| − | |||
| − | A further generalization of divisor problems is as follows [[#References|[4]]]: Uniformly with respect to the integers | + | for arbitrary $ \epsilon > 0 $, |
| + | $ \sigma > 1/2 $. | ||
| + | |||
| + | |||
| + | A further generalization of divisor problems is as follows [[#References|[4]]]: Uniformly with respect to the integers $ k \geq 2 $, | ||
| + | $ m \geq 1 $, | ||
| + | for $ x \geq 1 $ | ||
| + | one has | ||
| + | |||
| + | $$ | ||
| + | |||
| + | \frac{1}{x} | ||
| + | \sum _ {n \leq x} \tau _{k} ^{m} (n) | ||
| + | \ < \ A _{k} ^{(m)} ( \mathop{\rm ln}\nolimits \ x + k ^{m} - 1 ) ^ | ||
| + | {k ^{m} - 1} , | ||
| + | $$ | ||
| − | |||
where | where | ||
| − | + | $$ | |
| + | A _{k} ^{(m)} \ = \ | ||
| + | \frac{k ^ m}{( k ! ) ^ {( k ^{m} - 1 ) | ||
| + | / ( k - 1 )}} | ||
| + | . | ||
| + | $$ | ||
| + | |||
==The divisor problem in arithmetical progressions.== | ==The divisor problem in arithmetical progressions.== | ||
This is the problem of estimating the sums | This is the problem of estimating the sums | ||
| − | + | $$ | |
| + | \sum _ { {n \leq x , \atop n \equiv l \ ( { \mathop{\rm mod}\nolimits}\ d )}} | ||
| + | \tau _{k} ^{m} (n) \ = \ D _{k} ^{(m)} ( x; \ d,\ l ) , | ||
| + | $$ | ||
| − | |||
| − | + | uniformly with respect to $ x $, | |
| + | $ d $, | ||
| + | $ 0 \leq l \leq d $, | ||
| + | $ ( l,\ d ) = 1 $. | ||
| + | These sums were studied by analytical methods of the theory of $ L $- | ||
| + | functions, and are important to numerous problems in the theory of numbers [[#References|[7]]]. In the simplest case ( $ m=1 $) | ||
| + | asymptotic expressions have been obtained: | ||
| − | if | + | if $ k = 2 $, |
| + | for $ d \leq x ^{2/3} $( | ||
| + | cf. [[#References|[5]]]); | ||
| − | if | + | if $ k = 4 $, |
| + | for $ d \leq x ^{1/2} $( | ||
| + | cf. [[#References|[6]]]); | ||
| + | |||
| + | if $ k \geq 4 $, | ||
| + | for $ d \leq x ^{2/k} / \mathop{\rm ln}\nolimits ^{c} \ x $( | ||
| + | cf. [[#References|[8]]]). For any $ m\geq 1 $ | ||
| + | and $ k = 2 $, | ||
| + | the true order of growth ( $ tiltil $) | ||
| + | has been found [[#References|[9]]] for $ d \leq x ^ {1 - \alpha} $, | ||
| + | $ 0 < \alpha < 1/2 $: | ||
| + | |||
| + | |||
| + | $$ | ||
| + | D _{2} ^{(m)} ( x; \ d,\ l ) \ tiltil \ | ||
| + | \frac{x}{d} | ||
| + | |||
| + | \left [ \mathop{\rm ln}\nolimits \ | ||
| + | \frac{x}{d} | ||
| + | \prod _ {p \mid d} | ||
| + | \left ( 1 - | ||
| + | \frac{1}{p} | ||
| + | \right ) ^ {2 ^{m} -1} \right ] . | ||
| + | $$ | ||
| − | |||
In the general case it has been shown that [[#References|[10]]]: | In the general case it has been shown that [[#References|[10]]]: | ||
| − | + | $$ | |
| + | \sum _ {d \leq x ^ {1/2 - \epsilon}} \mathop{\rm max}\nolimits _{l} \ | | ||
| + | D _{k} ^{(m)} ( x; \ d,\ l ) - A _{k} ^{(m)} ( x; \ d ) | \ < \ | ||
| + | x ( \mathop{\rm ln}\nolimits \ x ) ^{-M} , | ||
| + | $$ | ||
| + | |||
| + | |||
| + | where $ A _{k} ^{(m)} ( x; \ d ) $ | ||
| + | is the expected principal term of growth, $ M $ | ||
| + | is a positive constant which may be arbitrary large, and $ \epsilon > 0 $ | ||
| + | is an arbitrary number. | ||
| − | + | The last inequality shows, in particular, that the sums $ D _{k} ^{(m)} ( x; \ d,\ l ) $, | |
| + | for any integers $ k \geq 2 $, | ||
| + | $ m \geq 1 $, | ||
| + | have, "on the average" , the same principal term of growth for all primitive arithmetical progressions with difference $ d \leq x ^ {1 / 2 - \epsilon} $. | ||
| − | |||
====References==== | ====References==== | ||
Revision as of 17:12, 28 January 2020
Problems in number theory concerned with the asymptotic behaviour of the summation functions
$$
D(x) = \sum_{n \le x} \tau(n)\ ,\ \ D_k(x) = \sum_{n \le x} \tau_k(n)
$$
where $\tau(n)$ is the number of divisors of $n$ and $\tau_k(n)$, $k \ge 2$, is the number of representations of $n$ as the product of $k$ natural numbers, as well as modifications of these functions.
Dirichlet's divisor problem.
This is the problem of the best estimate of the remainder term $\Delta(x)$ in the asymptotic formula $$ \sum_{n \le x} \tau(n) = x \log x + (2 \gamma - 1)x + \Delta(x) $$ where $\gamma$ is the Euler constant. The asymptotics of the sum $$ \sum_{n \le x} \tau(n) = D(x) $$ was first considered by P. Dirichlet in 1849. He based himself on the fact that this sum is equal to the number of points $(u,v)$ with positive integer coordinates under the hyperbola $uv = x$, and showed that $$ D(x) = x \log x + (2 \gamma - 1)x + O(\sqrt x) $$ This formula is known as Dirichlet's formula for the number of divisors.
The divisor problem was one of the models on which methods for estimating the number of integer points in expanding domains of various types were developed. Let $\theta$ be the greatest lower bound of the numbers $\alpha$ in the relation $\Delta(x) \ll x^\alpha$. According to Dirichlet, $\theta \le 1/2$. G.F. Voronoi proved that $\theta \le 1/3$. Later, the following estimates were obtained in succession: $$ \theta \le \frac{33}{100}\ ,\ \ \ \theta \le \frac{27}{82}\ ,\ \ \ \theta \le \frac{15}{46}\ ,\ \ \ \theta \le \frac{13}{40}\ . $$ The true order of the value of $\theta$ is unknown (1988). According to one hypothesis, $$ \Delta(x) \ll x^{1/4} \log^2 x \ . $$ On the other hand, it was proved by G.H. Hardy that $\theta \ge 1/4$ or, more exactly, that $$ \liminf \frac{\Delta(x)}{(x\log x)^{1/4}\log\log x} < 0 < \limsup \frac{\Delta(x)}{(x\log x)^{1/4}\log\log x} $$
In addition another formula, $$ \int_0^x \Delta(y)^2 dy = A x^{3/2} + O(x \log^5 x) $$ where $A$ is a constant, is known; this formula proves that the hypothesis on the order of $\Delta(x)$ is valid "on the average" .
The generalized divisor problem.
This is the problem of the best asymptotic expression for the sum
$$ \sum _ {n \leq x} \tau _{k} (n) \ = \ D _{k} (x) , $$
as $ x \rightarrow \infty $;
in particular, if $ k = 2 $,
$$
\tau _{2} (n) \ = \ \tau (n) ,\ \
D _{2} (x) \ = \ D (x) .
$$
The generalized divisor problem is closely connected with the behaviour of the Riemann zeta-function $ \zeta (s) $
in the critical strip of values of $ s $.
In fact, the following formula is valid for non-integer $ x > 0 $,
$ c > 1 $:
$$
D _{k} (x) \ = \
\frac{1}{2 \pi i}
\int\limits _ {c - i \infty} ^ {c + i \infty} \zeta ^{k} (s)
\frac{x ^ s}{s}
\ ds .
$$
Here, the integrand has at the point $ s = 1 $
a pole of order $ k $
with residue of the form $ xP _{k} ( \mathop{\rm ln}\nolimits \ x ) $
where $ P _{k} $
is a polynomial of degree $ k - 1 $.
Let
$$ D _{k} (x) \ = \ x P _{k} ( \mathop{\rm ln}\nolimits \ x ) + \Delta _{k} (x) $$
and let $ \gamma _{k} < \gamma < 1 $,
where $ \gamma _{k} $
is the greatest lower bound of the numbers $ \sigma $
for which
$$ \int\limits _ {- \infty} ^ \infty \frac{| \zeta ( \sigma + i t ) | ^ 2k}{| \sigma + i t | ^ 2} \ dt \ < \ \infty . $$
The following formulas are then valid:
$$ \Delta _{k} (x) \ = \ \frac{1}{2 \pi i} \lim _ {T \rightarrow \infty} \ \int\limits _ {\gamma - i T} ^ {\gamma + i T} \zeta ^{k} (s) \frac{x ^ s}{s} \ ds ; $$
and the inverse Mellin formula
$$ \frac{\zeta ^{k} (s)}{s} \ = \ \int\limits _{0} ^ \infty \Delta _{k} (x) x ^{-s-1} \ dx ,\ \ s = \sigma + i t , $$
where the integral exists in the mean-square sense for $ \gamma _{k} < \sigma < 1 $.
Estimates of the rest term $ \Delta _{k} (x) $
in the formula for $ D _{k} (x) $
are still (1988) far from what might be expected. Let $ \alpha _{k} $
be the smallest of the numbers $ \alpha $
for which
$$ \Delta _{k} (x) \ \ll \ x ^ {\alpha + \epsilon} $$
for any $ \epsilon > 0 $.
The following estimates are known:
$$ \alpha _{k} \ \leq \ \frac{k - 1}{k + 1} , $$
$$
\alpha _{k} \ \leq \
\frac{k - 1}{k + 2}
\ \ {\textrm{ for }} \ k \geq 4 .
$$
These estimates can be rendered more precise for individual values of $ k $:
$$
\alpha _{3} \ \leq \
\frac{37}{75}
,\ \ \alpha _{7} \ \leq \
\frac{71}{107}
,\ \
\alpha _{8} \ \leq \
\frac{41}{59}
,\ \ \alpha _{9} \ \leq \
\frac{26}{35}
,\ \
\alpha _{11} \ \leq \
\frac{19}{25}
.
$$
The last result giving an estimate from above for $ \alpha _{k} $
was obtained in [3] by developing the idea of the Vinogradov method: There is an absolute constant $ c > 0 $
such that
$$ \alpha _{k} \ \leq \ 1 - \frac{c}{k ^ 2/3} ,\ \ k = 2 ,\ 3 ,\dots . $$
This estimate follows from an estimate of $ \zeta (s) $
in the critical strip: For $ 1 / 2 \leq \sigma \leq 1 $,
$ | t | \geq 2 $
there is a constant $ a > 1 $
such that
$$ \zeta ( \sigma + i t ) \ \ll \ | t | ^ {a ( 1 - \sigma ) ^ 3/2} \mathop{\rm ln}\nolimits \ | t | . $$
On the other hand, it was shown by Hardy that
$$ \alpha _{k} \ \geq \ \frac{k - 1}{2k} . $$
Regarding the value of $ \Delta _{k} (x) $,
there is the hypothesis that
$$ \alpha _{k} \ = \ \frac{k - 1}{2k} $$
for all $ k \geq 2 $.
However, it cannot be justified, even not by solving the Lindelöf hypothesis:
$$ \zeta ( \sigma + i t ) \ \ll \ | t | ^ \epsilon $$
for arbitrary $ \epsilon > 0 $,
$ \sigma > 1/2 $.
A further generalization of divisor problems is as follows [4]: Uniformly with respect to the integers $ k \geq 2 $,
$ m \geq 1 $,
for $ x \geq 1 $
one has
$$ \frac{1}{x} \sum _ {n \leq x} \tau _{k} ^{m} (n) \ < \ A _{k} ^{(m)} ( \mathop{\rm ln}\nolimits \ x + k ^{m} - 1 ) ^ {k ^{m} - 1} , $$
where
$$ A _{k} ^{(m)} \ = \ \frac{k ^ m}{( k ! ) ^ {( k ^{m} - 1 ) / ( k - 1 )}} . $$
The divisor problem in arithmetical progressions.
This is the problem of estimating the sums
$$ \sum _ { {n \leq x , \atop n \equiv l \ ( { \mathop{\rm mod}\nolimits}\ d )}} \tau _{k} ^{m} (n) \ = \ D _{k} ^{(m)} ( x; \ d,\ l ) , $$
uniformly with respect to $ x $,
$ d $,
$ 0 \leq l \leq d $,
$ ( l,\ d ) = 1 $.
These sums were studied by analytical methods of the theory of $ L $-
functions, and are important to numerous problems in the theory of numbers [7]. In the simplest case ( $ m=1 $)
asymptotic expressions have been obtained:
if $ k = 2 $, for $ d \leq x ^{2/3} $( cf. [5]);
if $ k = 4 $, for $ d \leq x ^{1/2} $( cf. [6]);
if $ k \geq 4 $, for $ d \leq x ^{2/k} / \mathop{\rm ln}\nolimits ^{c} \ x $( cf. [8]). For any $ m\geq 1 $ and $ k = 2 $, the true order of growth ( $ tiltil $) has been found [9] for $ d \leq x ^ {1 - \alpha} $, $ 0 < \alpha < 1/2 $:
$$
D _{2} ^{(m)} ( x; \ d,\ l ) \ tiltil \
\frac{x}{d}
\left [ \mathop{\rm ln}\nolimits \
\frac{x}{d}
\prod _ {p \mid d}
\left ( 1 -
\frac{1}{p}
\right ) ^ {2 ^{m} -1} \right ] .
$$
In the general case it has been shown that [10]:
$$ \sum _ {d \leq x ^ {1/2 - \epsilon}} \mathop{\rm max}\nolimits _{l} \ | D _{k} ^{(m)} ( x; \ d,\ l ) - A _{k} ^{(m)} ( x; \ d ) | \ < \ x ( \mathop{\rm ln}\nolimits \ x ) ^{-M} , $$
where $ A _{k} ^{(m)} ( x; \ d ) $
is the expected principal term of growth, $ M $
is a positive constant which may be arbitrary large, and $ \epsilon > 0 $
is an arbitrary number.
The last inequality shows, in particular, that the sums $ D _{k} ^{(m)} ( x; \ d,\ l ) $, for any integers $ k \geq 2 $, $ m \geq 1 $, have, "on the average" , the same principal term of growth for all primitive arithmetical progressions with difference $ d \leq x ^ {1 / 2 - \epsilon} $.
References
| [1] | E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951) |
| [2] | L.-K. Hua, "Abschätzungen von Exponentialsummen und ihre Anwendung in der Zahlentheorie" , Enzyklopaedie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen , 1 : 2 (1959) (Heft 13, Teil 1) |
| [3] | A.A. Karatsuba, "Estimates for trigonometric sums by Vinogradov's method, and some applications" Proc. Steklov Inst. Math. , 112 (1973) pp. 251–265 Trudy. Mat. Inst. Steklov. , 112 (1971) pp. 241–255 |
| [4] | K.K. Mardzhanishvili, Dokl. Akad. Nauk SSSR , 22 (1939) pp. 391–393 |
| [5] | C. Hooley, "An asymptotic formula in the theory of numbers" Proc. London Math. Soc. (3) , 7 : 27 (1957) pp. 393–413 |
| [6] | Yu.V. Linnik, "All large numbers are sums of a prime and two squares. (A problem of Hardy and Littlewood) II" Mat. Sb. , 53 : 1 (1961) pp. 3–38 (In Russian) |
| [7] | Yu.V. Linnik, "The dispersion method in binary additive problems" , Amer. Math. Soc. (1963) (Translated from Russian) |
| [8] | A.F. Lavrik, "The functional equation for Dirichlet 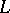 -functions and the divisor problem in arithmetical progressions" Izv. Akad. Nauk SSSR Ser. Mat. , 30 : 2 (1966) pp. 433–448 (In Russian) -functions and the divisor problem in arithmetical progressions" Izv. Akad. Nauk SSSR Ser. Mat. , 30 : 2 (1966) pp. 433–448 (In Russian) |
| [9] | A.I. Vinogradov, Yu.V. Linnik, "Estimate of the sum of the number of divisors in a short segment of an arithmetical progression" Uspekhi Mat. Nauk , 12 : 4 (1957) pp. 277–280 (In Russian) |
| [10] | A.I. Vinogradov, "On the density hypothesis for Dirichlet 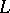 -series" Izv. Akad. Nauk SSSR Ser. Mat. , 29 : 4 (1965) pp. 903–934 (In Russian) -series" Izv. Akad. Nauk SSSR Ser. Mat. , 29 : 4 (1965) pp. 903–934 (In Russian) |
Comments
References
| [a1] | C. Hooley, "On a new technique and its applications to the theory of numbers" Proc. London Math. Soc. (3) , 38 (1979) pp. 115–151 |
| [a2] | K. Chandrasekharan, "Arithmetical functions" , Springer (1970) pp. Chapt. VIII |
Divisor problems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Divisor_problems&oldid=44350