Difference between revisions of "Dispersion relation"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | d0334001.png | ||
| + | $#A+1 = 13 n = 2 | ||
| + | $#C+1 = 13 : ~/encyclopedia/old_files/data/D033/D.0303400 Dispersion relation | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A relation connecting certain magnitudes which characterize the scattering of particles with magnitudes characterizing their absorption. More exactly, the dispersion relation is a relation connecting the real part of the scattering amplitude (in the more general case, the [[Green function|Green function]]) with certain types of integrals of its imaginary part. Let a function $ f ( t) $ | |
| + | be absolutely integrable on the axis, and let it satisfy the causal relation $ f ( t) = 0 $, | ||
| + | $ t < 0 $. | ||
| + | Then its Fourier–Laplace transform | ||
| − | + | $$ | |
| + | \widetilde{f} ( \zeta ) = \int\limits f ( t) e ^ {i \zeta t } dt , | ||
| + | \ \zeta = p + iq , | ||
| + | $$ | ||
| − | In describing real physical processes the dispersion relation of the type (*) becomes more complicated, since the function | + | will be a holomorphic function in the upper half-plane $ q > 0 $, |
| + | and the real and imaginary parts of the boundary value $ \widetilde{f} ( p) $ | ||
| + | will satisfy the dispersion relation | ||
| + | |||
| + | $$ \tag{* } | ||
| + | \mathop{\rm Re} \widetilde{f} ( p) = | ||
| + | \frac{1} \pi | ||
| + | v _ {p} \int\limits _ {- \infty } ^ \infty | ||
| + | |||
| + | \frac{ \mathop{\rm Im} \widetilde{f} ( p ^ \prime ) d p ^ \prime }{p ^ \prime - p } | ||
| + | . | ||
| + | $$ | ||
| + | |||
| + | In describing real physical processes the dispersion relation of the type (*) becomes more complicated, since the function $ \widetilde{f} ( \zeta ) $ | ||
| + | may increase at infinity as a polynomial (in this case a dispersion relation with subtractions is obtained), the boundary value $ \widetilde{f} ( p) $ | ||
| + | may be a generalized function of slow growth, while the number of variables may be more than one (multi-dimensional dispersion relations). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.N. Bogolyubov, B.V. Medvedev, M.K. Polivanov, "Questions in the theory of dispersion relations" , Moscow (1958) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N.N. Bogolyubov, A.A. Logunov, A.I. Oksak, I.T. Todorov, "General principles of quantum field theory" , Kluwer (1990) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.N. Bogolyubov, B.V. Medvedev, M.K. Polivanov, "Questions in the theory of dispersion relations" , Moscow (1958) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N.N. Bogolyubov, A.A. Logunov, A.I. Oksak, I.T. Todorov, "General principles of quantum field theory" , Kluwer (1990) (Translated from Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
A dispersion relation of the type defined here is often called a Kramers–Kronig relation. In the classical dispersion of light the relation gives a connection between the real (dispersive) and imaginary (absorptive) parts of the index of refraction. | A dispersion relation of the type defined here is often called a Kramers–Kronig relation. In the classical dispersion of light the relation gives a connection between the real (dispersive) and imaginary (absorptive) parts of the index of refraction. | ||
| − | Consider a linear wave equation such as the beam equation | + | Consider a linear wave equation such as the beam equation $ \phi _ {tt} + \gamma ^ {2} \phi _ {xxxx} = 0 $. |
| + | For a sinusoidal wave train $ \phi ( x , t ) = A \mathop{\rm exp} ( i k \cdot x - i \omega t ) $ | ||
| + | to satisfy such an equation some relation $ G ( k , \omega ) = 0 $ | ||
| + | between the frequency and the wave number must hold. In this case $ \omega ^ {2} - \gamma ^ {2} k ^ {4} = 0 $. | ||
| + | This relation is called the dispersion relation. There are generalizations to non-linear wave equations, e.g., the KdV-equation, where the dispersion relation also involves the amplitude. Dispersion relations for waves are extensively discussed in [[#References|[a5]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Kronig, ''J Opt. Soc. Amer'' , '''12''' (1926) pp. 547</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H.A. Kramers, , ''Atti. Congr. Intern. Fisici Como'' , '''2''' (1927) pp. 545</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> N.G. van Kampen, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033400/d03340014.png" />-matrix and causality condition I. Maxwell field" ''Phys. Rev.'' , '''89''' (1953) pp. 1072–1079</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> N.G. van Kampen, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033400/d03340015.png" />-matrix and causality condition II. Nonrelativistic particles" ''Phys. Rev.'' , '''91''' (1953) pp. 1267–1276</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Bremermann, "Distributions, complex variables, and Fourier transforms" , Addison-Wesley (1965)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> G.B. Whitham, "Linear and non-linear waves" , Wiley (1974)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Kronig, ''J Opt. Soc. Amer'' , '''12''' (1926) pp. 547</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H.A. Kramers, , ''Atti. Congr. Intern. Fisici Como'' , '''2''' (1927) pp. 545</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> N.G. van Kampen, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033400/d03340014.png" />-matrix and causality condition I. Maxwell field" ''Phys. Rev.'' , '''89''' (1953) pp. 1072–1079</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> N.G. van Kampen, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033400/d03340015.png" />-matrix and causality condition II. Nonrelativistic particles" ''Phys. Rev.'' , '''91''' (1953) pp. 1267–1276</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Bremermann, "Distributions, complex variables, and Fourier transforms" , Addison-Wesley (1965)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> G.B. Whitham, "Linear and non-linear waves" , Wiley (1974)</TD></TR></table> | ||
Revision as of 19:36, 5 June 2020
A relation connecting certain magnitudes which characterize the scattering of particles with magnitudes characterizing their absorption. More exactly, the dispersion relation is a relation connecting the real part of the scattering amplitude (in the more general case, the Green function) with certain types of integrals of its imaginary part. Let a function $ f ( t) $
be absolutely integrable on the axis, and let it satisfy the causal relation $ f ( t) = 0 $,
$ t < 0 $.
Then its Fourier–Laplace transform
$$ \widetilde{f} ( \zeta ) = \int\limits f ( t) e ^ {i \zeta t } dt , \ \zeta = p + iq , $$
will be a holomorphic function in the upper half-plane $ q > 0 $, and the real and imaginary parts of the boundary value $ \widetilde{f} ( p) $ will satisfy the dispersion relation
$$ \tag{* } \mathop{\rm Re} \widetilde{f} ( p) = \frac{1} \pi v _ {p} \int\limits _ {- \infty } ^ \infty \frac{ \mathop{\rm Im} \widetilde{f} ( p ^ \prime ) d p ^ \prime }{p ^ \prime - p } . $$
In describing real physical processes the dispersion relation of the type (*) becomes more complicated, since the function $ \widetilde{f} ( \zeta ) $ may increase at infinity as a polynomial (in this case a dispersion relation with subtractions is obtained), the boundary value $ \widetilde{f} ( p) $ may be a generalized function of slow growth, while the number of variables may be more than one (multi-dimensional dispersion relations).
References
| [1] | N.N. Bogolyubov, B.V. Medvedev, M.K. Polivanov, "Questions in the theory of dispersion relations" , Moscow (1958) (In Russian) |
| [2] | V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian) |
| [3] | N.N. Bogolyubov, A.A. Logunov, A.I. Oksak, I.T. Todorov, "General principles of quantum field theory" , Kluwer (1990) (Translated from Russian) |
Comments
A dispersion relation of the type defined here is often called a Kramers–Kronig relation. In the classical dispersion of light the relation gives a connection between the real (dispersive) and imaginary (absorptive) parts of the index of refraction.
Consider a linear wave equation such as the beam equation $ \phi _ {tt} + \gamma ^ {2} \phi _ {xxxx} = 0 $. For a sinusoidal wave train $ \phi ( x , t ) = A \mathop{\rm exp} ( i k \cdot x - i \omega t ) $ to satisfy such an equation some relation $ G ( k , \omega ) = 0 $ between the frequency and the wave number must hold. In this case $ \omega ^ {2} - \gamma ^ {2} k ^ {4} = 0 $. This relation is called the dispersion relation. There are generalizations to non-linear wave equations, e.g., the KdV-equation, where the dispersion relation also involves the amplitude. Dispersion relations for waves are extensively discussed in [a5].
References
| [a1] | R. Kronig, J Opt. Soc. Amer , 12 (1926) pp. 547 |
| [a2] | H.A. Kramers, , Atti. Congr. Intern. Fisici Como , 2 (1927) pp. 545 |
| [a3] | N.G. van Kampen, "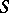 -matrix and causality condition I. Maxwell field" Phys. Rev. , 89 (1953) pp. 1072–1079 -matrix and causality condition I. Maxwell field" Phys. Rev. , 89 (1953) pp. 1072–1079 |
| [a4] | N.G. van Kampen, "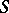 -matrix and causality condition II. Nonrelativistic particles" Phys. Rev. , 91 (1953) pp. 1267–1276 -matrix and causality condition II. Nonrelativistic particles" Phys. Rev. , 91 (1953) pp. 1267–1276 |
| [a5] | H. Bremermann, "Distributions, complex variables, and Fourier transforms" , Addison-Wesley (1965) |
| [a6] | G.B. Whitham, "Linear and non-linear waves" , Wiley (1974) |
Dispersion relation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dispersion_relation&oldid=12664