Difference between revisions of "Discrete subgroup"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Jon Awbrey (talk | contribs) (trying a bit of TeX conversion) |
||
| Line 1: | Line 1: | ||
{{TEX|want}} | {{TEX|want}} | ||
| − | A subgroup | + | A subgroup $\Gamma$ of a topological group $G$ (in particular, a subgroup of a Lie group) which is a discrete subset of the topological space $G$. In locally compact topological groups (in particular, in Lie groups) one distinguishes lattices — i.e. discrete subgroups for which the quotient space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d0331504.png" /> has finite volume in the sense of the measure induced by the left-invariant [[Haar measure|Haar measure]] on the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d0331505.png" />. The concept of lattices includes that of uniform discrete subgroups, for which the quotient space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d0331506.png" /> is compact. |
If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d0331507.png" /> is a compact subgroup of a locally compact topological group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d0331508.png" />, a subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d0331509.png" /> is discrete if and only if it is a [[Discrete group of transformations|discrete group of transformations]] of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d03315010.png" /> (in the sense of the action induced by the natural action of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d03315011.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d03315012.png" />). Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d03315013.png" /> is a lattice (a uniform discrete subgroup) if and only if the quotient space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d03315014.png" /> has finite volume (is compact) in the sense of the measure induced by the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d03315015.png" />-invariant measure on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d03315016.png" />. This makes it possible to utilize geometric methods when studying discrete subgroups of Lie groups. | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d0331507.png" /> is a compact subgroup of a locally compact topological group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d0331508.png" />, a subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d0331509.png" /> is discrete if and only if it is a [[Discrete group of transformations|discrete group of transformations]] of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d03315010.png" /> (in the sense of the action induced by the natural action of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d03315011.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d03315012.png" />). Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d03315013.png" /> is a lattice (a uniform discrete subgroup) if and only if the quotient space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d03315014.png" /> has finite volume (is compact) in the sense of the measure induced by the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d03315015.png" />-invariant measure on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033150/d03315016.png" />. This makes it possible to utilize geometric methods when studying discrete subgroups of Lie groups. | ||
Revision as of 03:36, 16 June 2012
A subgroup $\Gamma$ of a topological group $G$ (in particular, a subgroup of a Lie group) which is a discrete subset of the topological space $G$. In locally compact topological groups (in particular, in Lie groups) one distinguishes lattices — i.e. discrete subgroups for which the quotient space 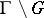 has finite volume in the sense of the measure induced by the left-invariant Haar measure on the group
has finite volume in the sense of the measure induced by the left-invariant Haar measure on the group 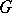 . The concept of lattices includes that of uniform discrete subgroups, for which the quotient space
. The concept of lattices includes that of uniform discrete subgroups, for which the quotient space 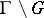 is compact.
is compact.
If 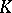 is a compact subgroup of a locally compact topological group
is a compact subgroup of a locally compact topological group 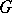 , a subgroup
, a subgroup 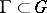 is discrete if and only if it is a discrete group of transformations of the space
is discrete if and only if it is a discrete group of transformations of the space 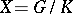 (in the sense of the action induced by the natural action of the group
(in the sense of the action induced by the natural action of the group 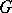 on
on 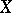 ). Here,
). Here, 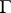 is a lattice (a uniform discrete subgroup) if and only if the quotient space
is a lattice (a uniform discrete subgroup) if and only if the quotient space 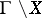 has finite volume (is compact) in the sense of the measure induced by the
has finite volume (is compact) in the sense of the measure induced by the 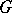 -invariant measure on
-invariant measure on  . This makes it possible to utilize geometric methods when studying discrete subgroups of Lie groups.
. This makes it possible to utilize geometric methods when studying discrete subgroups of Lie groups.
One of the principal problems in the theory of discrete subgroups of Lie groups is the classification of such subgroups up to commensurability. Two subgroups 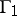 and
and 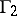 are said to be commensurable if
are said to be commensurable if  has finite index both in
has finite index both in 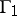 and in
and in 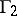 . If one of two commensurable subgroups of a locally compact topological group is a discrete subgroup (or a lattice, or a uniform discrete subgroup), so is the other.
. If one of two commensurable subgroups of a locally compact topological group is a discrete subgroup (or a lattice, or a uniform discrete subgroup), so is the other.
Up to the middle of the 20th century one basically studied individual classes of discrete subgroups of Lie groups occurring in arithmetic, function theory and physics. Historically, the first non-trivial discrete subgroup — the subgroup 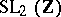 of the group
of the group 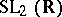 , subsequently named the Kleinian modular group — was in fact studied by J.L. Lagrange and C.F. Gauss in the context of the arithmetic of quadratic forms in two variables. The subgroup
, subsequently named the Kleinian modular group — was in fact studied by J.L. Lagrange and C.F. Gauss in the context of the arithmetic of quadratic forms in two variables. The subgroup 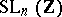 of
of 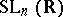 is its natural generalization. The study of this group as a discrete group of transformations of the space of positive-definite quadratic forms in
is its natural generalization. The study of this group as a discrete group of transformations of the space of positive-definite quadratic forms in  variables formed the subject of reduction theory, developed by A.N. Korkin, E.I. Zolotarev, Ch. Hermite, H. Minkowski, and others in the second half of the nineteenth and in the beginning of the 20th century. A series of arithmetically definable discrete subgroups of classical Lie groups — groups of units of quadratic forms with rational coefficients, groups of units of simple algebras over
variables formed the subject of reduction theory, developed by A.N. Korkin, E.I. Zolotarev, Ch. Hermite, H. Minkowski, and others in the second half of the nineteenth and in the beginning of the 20th century. A series of arithmetically definable discrete subgroups of classical Lie groups — groups of units of quadratic forms with rational coefficients, groups of units of simple algebras over 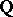 , groups of integral symplectic matrices — were studied by C.L. Siegel in the 1940s. He proved, in particular, that all these groups are lattices in the respective Lie groups.
, groups of integral symplectic matrices — were studied by C.L. Siegel in the 1940s. He proved, in particular, that all these groups are lattices in the respective Lie groups.
In the theory of functions of a complex variable the integration of algebraic functions and, more generally, the solution of differential equations with algebraic coefficients, resulted in the study of certain special functions (subsequently named automorphic functions, cf. Automorphic function) which are invariant with respect to various discrete groups consisting of transformations of the form
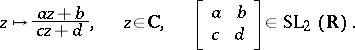 | (1) |
Certain discrete subgroups of 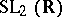 were studied in the mid-19th century by Hermite, R. Dedekind and I.L. Fuchs. They also included the group
were studied in the mid-19th century by Hermite, R. Dedekind and I.L. Fuchs. They also included the group 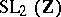 (though represented differently from the presentation used by Lagrange and Gauss). A wide class of such groups, including the group
(though represented differently from the presentation used by Lagrange and Gauss). A wide class of such groups, including the group 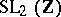 and certain subgroups of
and certain subgroups of 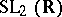 commensurable with it, were studied by F. Klein. Almost simultaneously (1881–1882) H. Poincaré gave a geometric description of all discrete groups consisting of transformations of the form (1). He named these groups Fuchsian groups (cf. Fuchsian group).
commensurable with it, were studied by F. Klein. Almost simultaneously (1881–1882) H. Poincaré gave a geometric description of all discrete groups consisting of transformations of the form (1). He named these groups Fuchsian groups (cf. Fuchsian group).
In the first half of the 20th century studies were made of individual classes of automorphic functions in several variables. These functions were connected with certain arithmetically definable discrete subgroups of the group 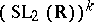 (Hilbert's modular functions),
(Hilbert's modular functions), 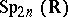 (Siegel's modular functions) and other semi-simple Lie groups.
(Siegel's modular functions) and other semi-simple Lie groups.
Since the late 19th century, crystallographic studies have centred on the symmetry groups of crystallographic lattices, which are identical with uniform discrete subgroups of the group of motions of three-dimensional Euclidean space. These, together with the related groups of motions of  -dimensional Euclidean space (the so-called crystallographic groups, cf. Crystallographic group) were studied in 1911 by L. Bieberbach from the algebraic point of view. He demonstrated, in particular, the theorem according to which any crystallographic group contains a uniform discrete subgroup of parallel translations.
-dimensional Euclidean space (the so-called crystallographic groups, cf. Crystallographic group) were studied in 1911 by L. Bieberbach from the algebraic point of view. He demonstrated, in particular, the theorem according to which any crystallographic group contains a uniform discrete subgroup of parallel translations.
All these studies provided the initial material for the general theory of discrete subgroups of Lie groups, the foundations of which were laid in the 1950s and 1960s.
An exhaustive theory of discrete subgroups of nilpotent Lie groups has been constructed [9]. Its main statements are listed below: 1) If 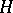 is a unipotent algebraic group defined over
is a unipotent algebraic group defined over 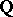 , then the group
, then the group 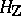 of its integer points is a uniform discrete subgroup in the group
of its integer points is a uniform discrete subgroup in the group 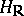 of its real points. (Here
of its real points. (Here 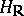 is a simply-connected nilpotent Lie group.) 2) Any uniform discrete subgroup
is a simply-connected nilpotent Lie group.) 2) Any uniform discrete subgroup 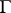 of a simply-connected nilpotent Lie group
of a simply-connected nilpotent Lie group 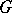 is arithmetic in the sense that there exist a unipotent algebraic group
is arithmetic in the sense that there exist a unipotent algebraic group 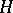 defined over
defined over 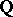 and an isomorphism
and an isomorphism 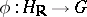 such that the subgroup
such that the subgroup 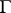 is commensurable with
is commensurable with 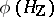 . 3) If
. 3) If 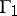 ,
, 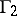 are uniform discrete subgroups of simply-connected nilpotent Lie groups
are uniform discrete subgroups of simply-connected nilpotent Lie groups 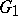 and
and 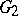 respectively, then any isomorphism
respectively, then any isomorphism 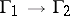 can be uniquely extended to an isomorphism
can be uniquely extended to an isomorphism 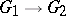 . 4) An abstract group
. 4) An abstract group 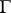 is imbeddable as a uniform discrete subgroup in a simply-connected nilpotent Lie group if and only if
is imbeddable as a uniform discrete subgroup in a simply-connected nilpotent Lie group if and only if 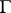 is a finitely-generated torsion-free nilpotent group.
is a finitely-generated torsion-free nilpotent group.
Discrete subgroups of solvable Lie groups have been fairly thoroughly studied, but the results are less complete than those obtained for nilpotent groups. Any lattice in a solvable Lie group is a uniform discrete subgroup. If 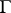 is a lattice in a simply-connected solvable Lie group
is a lattice in a simply-connected solvable Lie group 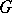 , then
, then 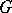 has a faithful matrix representation in which the elements of
has a faithful matrix representation in which the elements of 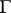 are represented by integer matrices [13]. This statement may be regarded as a generalization of Mal'tsev's theorem 2) above. The following theorem is the analogue of theorem 4). Any lattice in a simply-connected solvable Lie group is a strictly polycyclic group; conversely, any strictly polycyclic group has a subgroup of finite index which is isomorphic to a lattice in a simply-connected solvable Lie group.
are represented by integer matrices [13]. This statement may be regarded as a generalization of Mal'tsev's theorem 2) above. The following theorem is the analogue of theorem 4). Any lattice in a simply-connected solvable Lie group is a strictly polycyclic group; conversely, any strictly polycyclic group has a subgroup of finite index which is isomorphic to a lattice in a simply-connected solvable Lie group.
The most precise results in the theory of discrete subgroups of Lie groups concern discrete subgroups of non-solvable and, in particular, semi-simple Lie groups. In [4] the following theorem was demonstrated, which includes, as special cases, Mal'tsev's theorem 1), the Dirichlet theorem on the units of an algebraic number field and Siegel's results (see above) on certain arithmetic discrete subgroups of semi-simple Lie groups. Let 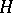 be a linear algebraic group defined over
be a linear algebraic group defined over 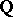 . For the subgroup
. For the subgroup 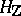 to be a lattice in
to be a lattice in 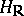 it is necessary and sufficient for
it is necessary and sufficient for  not to permit rational homomorphisms into the group
not to permit rational homomorphisms into the group 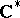 , defined over
, defined over 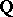 (this condition is satisfied, for example, if
(this condition is satisfied, for example, if 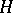 is semi-simple or unipotent). For the subgroup
is semi-simple or unipotent). For the subgroup 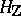 to be a uniform discrete subgroup in
to be a uniform discrete subgroup in 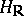 it is necessary and sufficient, in addition, that all unipotent elements of the group
it is necessary and sufficient, in addition, that all unipotent elements of the group 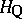 lie in
lie in 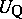 , where
, where 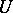 is the unipotent radical of
is the unipotent radical of 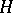 .
.
The arithmeticity theorem [11] which follows is the analogue of theorem 2) for discrete subgroups of semi-simple Lie groups. Let 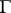 be a lattice in a connected semi-simple Lie group
be a lattice in a connected semi-simple Lie group 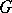 without compact factors, and let (for the sake of convenience in formulation) the centre of
without compact factors, and let (for the sake of convenience in formulation) the centre of 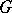 be trivial. Moreover, let the lattice
be trivial. Moreover, let the lattice 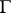 be irreducible in the sense that
be irreducible in the sense that 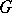 cannot be non-trivially decomposed into a direct product
cannot be non-trivially decomposed into a direct product 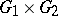 so that
so that 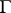 is commensurable with a subgroup of the form
is commensurable with a subgroup of the form 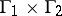 where
where 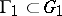 and
and 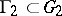 . Then, if the real rank of
. Then, if the real rank of 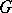 exceeds one, the group
exceeds one, the group  is arithmetic in the sense that there exist a semi-simple algebraic group
is arithmetic in the sense that there exist a semi-simple algebraic group 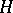 , defined over
, defined over 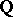 , and a homomorphism
, and a homomorphism 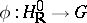 (where
(where 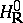 is the connected component of the unit of the group
is the connected component of the unit of the group 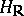 ) such that the kernel of the homomorphism
) such that the kernel of the homomorphism 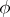 is compact and the subgroup
is compact and the subgroup 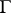 is commensurable with
is commensurable with 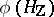 . The assumption that the real rank of
. The assumption that the real rank of 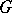 exceeds one is essential. It is known that the theorem is invalid for the group
exceeds one is essential. It is known that the theorem is invalid for the group 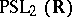 (the group of motions of the Lobachevskii plane), which on the whole plays an important role in the theory of discrete subgroups of Lie groups, and also for the groups of motions of the three-, four- and five-dimensional Lobachevskii spaces [6], [8].
(the group of motions of the Lobachevskii plane), which on the whole plays an important role in the theory of discrete subgroups of Lie groups, and also for the groups of motions of the three-, four- and five-dimensional Lobachevskii spaces [6], [8].
The strong rigidity theorem which follows is the analogue of theorem 3) for discrete subgroups of semi-simple Lie groups. Let 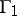 ,
, 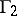 be irreducible lattices in connected semi-simple Lie groups
be irreducible lattices in connected semi-simple Lie groups 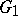 ,
, 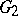 without compact factors, and let the centres of
without compact factors, and let the centres of 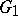 ,
, 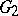 be trivial. Then, if
be trivial. Then, if 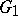 and
and 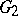 are not isomorphic to
are not isomorphic to 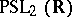 , any isomorphism
, any isomorphism 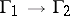 can be uniquely extended to an isomorphism
can be uniquely extended to an isomorphism 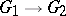 [10], [14]. Historically, the proof of this theorem was preceded by the proof of the weak rigidity theorem
[10], [14]. Historically, the proof of this theorem was preceded by the proof of the weak rigidity theorem
on the extension of isomorphisms which are sufficiently close to the identity (if 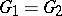 ). One consequence of the weak rigidity theorem is the existence of a basis in which the elements of a discrete subgroup are written in the form of algebraic numbers. This fact played an important role in the development of the theory of discrete subgroups of semi-simple Lie groups.
). One consequence of the weak rigidity theorem is the existence of a basis in which the elements of a discrete subgroup are written in the form of algebraic numbers. This fact played an important role in the development of the theory of discrete subgroups of semi-simple Lie groups.
Regarding discrete subgroups of the group 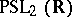 see Fuchsian group.
see Fuchsian group.
Of the other general theorems about discrete subgroups of semi-simple Lie groups one may mention Borel's density theorem and Wang's maximality theorem. Let 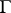 be a lattice in a connected semi-simple Lie group
be a lattice in a connected semi-simple Lie group 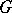 which has no compact factors. Then
which has no compact factors. Then 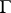 is dense in
is dense in 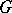 in the Zariski topology [3], and is contained in only a finite number of lattices in
in the Zariski topology [3], and is contained in only a finite number of lattices in 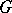 [17].
[17].
The description of lattices in arbitrary Lie groups can be reduced, to some extent, to the description of lattices in semi-simple Lie groups, in view of theorems analogous to the Bieberbach theorem on crystallographic groups mentioned above. One says that a normal subgroup 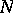 of a Lie group
of a Lie group 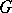 has the Bieberbach property if for any lattice
has the Bieberbach property if for any lattice 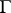 in
in 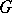 the subgroup
the subgroup 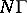 is closed (and, in such a case,
is closed (and, in such a case, 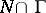 is automatically a lattice in
is automatically a lattice in 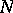 , while
, while 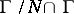 is a lattice in
is a lattice in 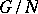 ). Bieberbach's theorem says that, in the group of motions of Euclidean space, the subgroup of parallel translations has the Bieberbach property. There exists a generalization of this theorem to Lie groups which are extensions of a simply-connected nilpotent Lie group by a compact group [1]. Another theorem of such a type is the following. Let
). Bieberbach's theorem says that, in the group of motions of Euclidean space, the subgroup of parallel translations has the Bieberbach property. There exists a generalization of this theorem to Lie groups which are extensions of a simply-connected nilpotent Lie group by a compact group [1]. Another theorem of such a type is the following. Let 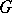 be a connected Lie group, let
be a connected Lie group, let 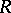 be its radical, let
be its radical, let 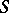 be a maximal connected semi-simple subgroup, and let
be a maximal connected semi-simple subgroup, and let 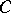 be a maximal connected compact normal subgroup of
be a maximal connected compact normal subgroup of 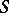 . Then the subgroup
. Then the subgroup 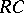 has the Bieberbach property in
has the Bieberbach property in 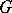 [2]. It is also known that the Bieberbach property is displayed by the nilpotent radical of a connected solvable Lie group [12] and by the commutator subgroup of a simply-connected nilpotent Lie group [9].
[2]. It is also known that the Bieberbach property is displayed by the nilpotent radical of a connected solvable Lie group [12] and by the commutator subgroup of a simply-connected nilpotent Lie group [9].
Topological methods (cf. Discrete group of transformations) can be used to prove that any uniform discrete subgroup of a connected Lie group is a finitely-presentable group . In fact, any lattice in a connected Lie group is finitely presentable [17], [18].
References
| [1] | L. Auslander, "Bieberbach's theorem on space groups and discrete uniform subgroups of Lie groups" Amer. J. Math. , 83 (1961) pp. 276–280 MR123637 |
| [2] | L. Auslander, "On radicals of discrete subgroups of Lie groups" Amer. J. Math. , 85 (1963) pp. 145–150 MR0152607 Zbl 0217.37002 |
| [3] | A. Borel, "Density properties for certain subgroups of semi-simple groups without compact components" Ann. of Math. , 72 (1960) pp. 179–188 MR0123639 Zbl 0094.24901 |
| [4] | A. Borel, Harish-Chandra, "Arithmetic subgroups of algebraic groups" Ann. of Math. , 75 (1962) pp. 485–535 MR0147566 Zbl 0107.14804 |
| [5a] | A. Weil, "Discrete subgroups of Lie groups I" Ann. Math. , 72 (1960) pp. 369–384 MR137792 Zbl 0131.26602 |
| [5b] | A. Weil, "Discrete subgroups of Lie groups II" Ann. Math. , 75 (1962) pp. 578–602 MR0137793 Zbl 0131.26602 |
| [6] | E.B. Vinberg, "Discrete groups generated by reflections in Lobachevskii spaces" Math. USSR-Sb. , 1 : 3 (1967) pp. 429–444 Mat. Sb. , 72 : 3 (1967) pp. 471–488 |
| [7] | H. Garland, M.S. Raghunathan, "Fundamental domains for lattices in (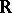 -) rank 1 semisimple Lie groups" Ann. of Math. , 92 (1970) pp. 279–326 MR267041 -) rank 1 semisimple Lie groups" Ann. of Math. , 92 (1970) pp. 279–326 MR267041 |
| [8] | V.S. Makarov, "A certain class of discrete Lobachevskii space groups with an infinite fundamental region of finite measure" Soviet Math.-Dokl. , 7 (1966) pp. 328–331 Dokl. Akad. Nauk. SSSR , 167 : 1 (1966) pp. 30–33 |
| [9] | A.I. Mal'tsev, "On a class of homogeneous spaces" Izv. Akad. Nauk. SSSR Ser. Mat. , 13 : 1 (1949) pp. 9–32 (In Russian) Zbl 0034.01701 |
| [10] | G.A. Margulis, "Arithmetic properties of discrete subgroups" Russian Math. Surveys , 29 : 1 (1974) pp. 107–156 Uspekhi Mat. Nauk , 29 : 1 (1974) pp. 49–98 MR0463353 MR0463354 Zbl 0299.22010 |
| [11] | G.A. Margulis, "Discrete groups of motions of manifolds of non-positive curvature" R. James (ed.) , Proc. Internat. Congress Mathematicians (Vancouver, 1974) , 2 , Canad. Math. Congress (1975) pp. 21–34 (In Russian) MR492072 Zbl 0336.57037 |
| [12] | G.D. Mostow, "Factor spaces of solvable groups" Ann. of Math. , 60 (1954) pp. 1–27 MR0061611 Zbl 0057.26103 |
| [13] | G.D. Mostov, "Representative functions on discrete groups and solvable arithmetic subgroups" Amer. J. Math. , 92 (1970) pp. 1–32 |
| [14] | G.D. Mostow, "Strong rigidity of locally symmetric spaces" , Princeton Univ. Press (1973) MR0385004 Zbl 0265.53039 |
| [15] | M.S. Raghunathan, "Discrete subgroups of Lie groups" , Springer (1972) MR0507234 MR0507236 Zbl 0254.22005 |
| [16] | A. Selberg, "On discontinuous groups in higher-dimensional symmetric spaces" , Internat. Coll. function theory , Tata Inst. (1960) pp. 147–164 MR0130324 Zbl 0201.36603 |
| [17] | H.-C. Wang, "On a maximality property of subgroups with fundamental domain of finite measure" Amer. J. Math. , 89 (1967) pp. 124–132 Zbl 0152.01002 |
| [18] | H.-C. Wang, "Topics on totally discontinuous groups" , Symmetric spaces , M. Dekker (1972) pp. 459–487 MR0414787 Zbl 0232.22018 |
Comments
The arithmeticity theorem, mentioned in the main article and saying that an irreducible lattice 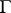 in a connected semi-simple Lie group
in a connected semi-simple Lie group 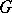 without compact factors (and with trivial centre) is an arithmetic group if the real rank of
without compact factors (and with trivial centre) is an arithmetic group if the real rank of 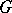 exceeds one, was conjectured by A. Selberg (for uniform discrete subgroups) and by I.I. Pyatetskii-Shapiro (general case), see also [a1]. A first important step to the understanding of non-compact subgroups
exceeds one, was conjectured by A. Selberg (for uniform discrete subgroups) and by I.I. Pyatetskii-Shapiro (general case), see also [a1]. A first important step to the understanding of non-compact subgroups 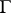 of finite co-volume, i.e.
of finite co-volume, i.e. 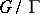 of finite volume, was the proof by D.A. Kazhdan and G.A. Margulis of the existence of non-trivial unipotent elements in
of finite volume, was the proof by D.A. Kazhdan and G.A. Margulis of the existence of non-trivial unipotent elements in 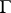 ; this is a related, more special, conjecture of Selberg, cf. [a5]. In [a2] it is proved that this theorem does not hold for the groups
; this is a related, more special, conjecture of Selberg, cf. [a5]. In [a2] it is proved that this theorem does not hold for the groups 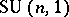 ,
, 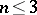 .
.
Ergodic theory plays an important role in proving some of the arithmeticity results mentioned in the main article, cf. also [a3]. One result in the proof of which ergodic arguments play an important role (the multiplicative ergodic theorem) is Margulis' superrigidity theorem, which for groups of real rank 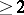 generalizes the A. Weil and G.D. Mostow rigidity theorems. It states the following. Let
generalizes the A. Weil and G.D. Mostow rigidity theorems. It states the following. Let 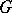 be a simply-connected Lie group of real points of a real simply-connected algebraic group
be a simply-connected Lie group of real points of a real simply-connected algebraic group 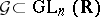 and let
and let 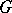 have no compact factors. Assume that the real rank of
have no compact factors. Assume that the real rank of 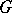 is
is 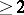 . Let
. Let 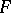 be a locally compact non-discrete field and
be a locally compact non-discrete field and 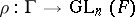 a linear representation such that
a linear representation such that 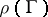 is not relatively compact and such that its Zariski closure is connected. Then
is not relatively compact and such that its Zariski closure is connected. Then 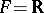 or
or 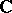 and
and 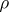 extends to a rational representation of
extends to a rational representation of 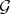 , cf. [a6] for a detailed discussion of these results and related matters; cf. also the discussion on strong rigidity in the main article above.
, cf. [a6] for a detailed discussion of these results and related matters; cf. also the discussion on strong rigidity in the main article above.
References
| [a1] | G.A. Margulus, "Arithmeticity of irreducible lattices in semi-simple groups of rank exceeding 1" , MIR (1977) (In Russian) (Appendix to the Russian translation of: M.S. Raghunathan: "On the congruence subgroup problem" Publ. Math. IHES  (1976), 107–161) (1976), 107–161) |
| [a2] | G.D. Mostow, "Existence of nonarithmetic monodromy groups" Proc. Nat. Acad. Sc. U.S.A. , 78 (1981) pp. 5948–5950 MR0773821 Zbl 0551.32024 |
| [a3] | R.J. Zimmer, "Ergodic theory and semisimple groups" , Birkhäuser (1984) MR0776417 Zbl 0571.58015 |
| [a4] | J.E. Humphreys, "Arithmetic groups" , Topics in the theory of arithmetic groups , Notre Dame Univ. (1982) pp. 73–97 MR0698787 Zbl 0504.22010 |
| [a5] | D.A. Kazhdan, G.A. Margulis, "A proof of Selberg's conjecture" Math. USSR-Sb. , 4 : 1 (1968) pp. 147–152 Mat. Sb. , 75 (1968) pp. 163–168 |
| [a6] | J. Tits, "Travaux de Margulis sur les sous-groupes discrets de groupes de Lie" , Sem. Bourbaki 1975/1976 , Exp. 482 , Springer (1977) pp. 174–190 MR0492073 Zbl 0346.22011 |
Discrete subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Discrete_subgroup&oldid=27025