Difference between revisions of "Discrete group of transformations"
(Importing text file) |
m (→References: latexify) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | d0330801.png | ||
| + | $#A+1 = 153 n = 2 | ||
| + | $#C+1 = 153 : ~/encyclopedia/old_files/data/D033/D.0303080 Discrete group of transformations | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| + | |||
| + | A group $ \Gamma $ | ||
| + | of homeomorphisms of a Hausdorff space $ X $ | ||
| + | that satisfies the following condition: It is possible to find neighbourhoods $ U , V $ | ||
| + | of arbitrary points $ x , y \in X $ | ||
| + | such that the set | ||
| + | |||
| + | $$ | ||
| + | \{ {\gamma \in \Gamma } : {\gamma ( U) \cap V \neq \emptyset } \} | ||
| + | $$ | ||
is finite. The stabilizer | is finite. The stabilizer | ||
| − | + | $$ | |
| + | \Gamma _ {x} = \{ {\gamma \in \Gamma } : {\gamma ( x) = x } \} | ||
| + | $$ | ||
| − | of a point | + | of a point $ x \in X $ |
| + | with respect to a discrete group of transformations is finite, while the orbit of an arbitrary point $ x \in X $ | ||
| + | is discrete. If $ X $ | ||
| + | is a metric space and the transformations from $ \Gamma $ | ||
| + | are isometries, these two conditions are sufficient for $ \Gamma $ | ||
| + | to be a discrete group of transformations. | ||
===Examples.=== | ===Examples.=== | ||
| + | 1) The group of parallel translations of the real plane $ \mathbf R ^ {2} $ | ||
| + | over all possible integer vectors: | ||
| − | + | $$ | |
| − | + | ( x , y) \rightarrow ( x + n , y + m ) ,\ \ | |
| − | + | ( x , y) \in \mathbf R ^ {2} ; \ n , m \in \mathbf Z . | |
| + | $$ | ||
| − | 2) Let | + | 2) Let $ X $ |
| + | be the complex upper half-plane | ||
| − | + | $$ | |
| + | \mathbf C ^ {+} = \{ {z \in \mathbf C } : { \mathop{\rm Im} z > 0 } \} | ||
| + | , | ||
| + | $$ | ||
| − | considered with the ordinary Hausdorff topology, and let | + | considered with the ordinary Hausdorff topology, and let $ \Gamma $ |
| + | be the group of Möbius transformations of the form | ||
| − | + | $$ | |
| + | z \rightarrow | ||
| + | \frac{a z + b }{c z + d } | ||
| + | , | ||
| + | $$ | ||
| − | where | + | where $ a $, |
| + | $ b $, | ||
| + | $ c $, | ||
| + | and $ d $ | ||
| + | are integers and $ ad - bc = 1 $( | ||
| + | the Kleinian modular group). | ||
| − | 3) Any finite group | + | 3) Any finite group $ \Gamma $ |
| + | of homeomorphisms of a Hausdorff space $ X $. | ||
| + | (The example of an irreducible algebraic variety with the Zariski topology shows that the condition of separability of $ X $ | ||
| + | is essential.) | ||
| − | 4) The [[Group of covering transformations|group of covering transformations]] of an arbitrary regular covering | + | 4) The [[Group of covering transformations|group of covering transformations]] of an arbitrary regular covering $ p : X \rightarrow Y $, |
| + | where $ X $ | ||
| + | is connected and locally path-connected, while $ Y $ | ||
| + | is a Hausdorff space, is a freely-acting (i.e. $ \Gamma _ {x} = \{ 1 \} $ | ||
| + | for any $ x \in X $) | ||
| + | discrete group of transformations; the covering $ p $ | ||
| + | itself coincides with the mapping of factorization by this group. Conversely, if $ \Gamma $ | ||
| + | is a freely-acting discrete group of transformations of a connected topological space $ X $, | ||
| + | then the quotient space $ X / \Gamma $ | ||
| + | is a Hausdorff space, and the quotient mapping $ p : X \rightarrow X / \Gamma $ | ||
| + | is a regular covering of $ X / \Gamma $ | ||
| + | with $ \Gamma $ | ||
| + | as group of covering transformations. In particular, by virtue of the Poincaré–Koebe uniformization theorem, any Riemann surface, apart from a few trivial exceptions, may be obtained by factorization of the complex upper half-plane $ \mathbf C ^ {+} $ | ||
| + | by a freely-acting discrete group of Möbius transformations with real coefficients (a so-called [[Fuchsian group|Fuchsian group]]). | ||
5) In the theory of moduli of Riemann surfaces (and, more generally, of moduli of complex manifolds of some given type), discrete groups of transformations appear as modular groups (cf. [[Modular group|Modular group]]). The simplest such group is discussed in Example 2. | 5) In the theory of moduli of Riemann surfaces (and, more generally, of moduli of complex manifolds of some given type), discrete groups of transformations appear as modular groups (cf. [[Modular group|Modular group]]). The simplest such group is discussed in Example 2. | ||
| Line 34: | Line 92: | ||
6) Discrete groups of transformations include the crystallographic groups (cf. [[Crystallographic group|Crystallographic group]]). A fairly wide class of discrete groups of transformations, which includes Fuchsian and crystallographic groups, is constituted by discrete subgroups (cf. [[Discrete subgroup|Discrete subgroup]]) of topological groups (in particular, of Lie groups), considered as groups of transformations of homogeneous spaces. | 6) Discrete groups of transformations include the crystallographic groups (cf. [[Crystallographic group|Crystallographic group]]). A fairly wide class of discrete groups of transformations, which includes Fuchsian and crystallographic groups, is constituted by discrete subgroups (cf. [[Discrete subgroup|Discrete subgroup]]) of topological groups (in particular, of Lie groups), considered as groups of transformations of homogeneous spaces. | ||
| − | A closed subset | + | A closed subset $ D $ |
| + | of a topological space $ X $ | ||
| + | with a discrete group $ \Gamma $ | ||
| + | of transformations is called a fundamental domain of the group $ \Gamma $ | ||
| + | if it is the closure of an open subset and if the sets $ \gamma ( D) $ | ||
| + | where $ \gamma \in \Gamma $ | ||
| + | have pairwise no common interior points and form a locally finite covering of $ X $. | ||
| + | For instance, for the group of parallel translations in Example 1, the square | ||
| − | + | $$ \tag{* } | |
| + | \{ {( x , y ) \in \mathbf R ^ {2} } : {0 \leq x \leq 1 , 0 \leq y \leq 1 } \} | ||
| + | $$ | ||
may be taken as a fundamental domain; the same purpose will be served by any parallelogram with vertices at integral points which has no integral points inside or on the sides, while in the case of a Kleinian modular group (Example 2) one may take the so-called modular figure | may be taken as a fundamental domain; the same purpose will be served by any parallelogram with vertices at integral points which has no integral points inside or on the sides, while in the case of a Kleinian modular group (Example 2) one may take the so-called modular figure | ||
| − | + | $$ | |
| + | D = \left \{ {z \in \mathbf C ^ {+} } : {- | ||
| + | \frac{1}{2} | ||
| + | \leq \mathop{\rm Re} z | ||
| + | \leq | ||
| + | \frac{1}{2} | ||
| + | , | z | \geq 1 } \right \} | ||
| + | . | ||
| + | $$ | ||
| − | In many cases a fundamental domain can be constructed. For instance, if | + | In many cases a fundamental domain can be constructed. For instance, if $ X $ |
| + | is a complete Riemannian manifold, if $ \Gamma $ | ||
| + | is the discrete group of transformations of $ X $ | ||
| + | consisting of the isometries of this space, and if $ x _ {0} \in X $ | ||
| + | is some point for which the stabilizer $ \Gamma _ {x _ {0} } $ | ||
| + | is trivial, then the Dirichlet domain | ||
| − | + | $$ | |
| + | D = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | \{ {x \in X } : {d ( x, x _ {0} ) \leq d ( x | ||
| + | , \gamma ( x _ {0} ) ) \textrm{ for all } | ||
| + | \textrm{ non\AAh identity transformations } \gamma \in \Gamma } \} | ||
| + | $$ | ||
| − | may be taken as a fundamental domain. In the above formula | + | may be taken as a fundamental domain. In the above formula $ d ( x , y ) $ |
| + | denotes the distance between two points $ x $ | ||
| + | and $ y $ | ||
| + | from $ X $. | ||
| + | If $ X $ | ||
| + | is a simply-connected complete space of constant curvature, i.e. a sphere, a Euclidean space or a Lobachevskii space, a Dirichlet domain is a convex polyhedron. | ||
| − | The construction of a fundamental domain and the study of its properties furnish important information about the discrete group of transformations. Thus, the quotient space | + | The construction of a fundamental domain and the study of its properties furnish important information about the discrete group of transformations. Thus, the quotient space $ X / \Gamma $ |
| + | is obtained from a fundamental domain by way of "glueing" certain boundary points. For example, the quotient space of the group of parallel translations (Example 1) is obtained from the square (*) by glueing the opposite sides and is homeomorphic to a two-dimensional torus. The concept of a fundamental domain forms the base of the combinatorial-geometric method in the theory of discrete groups of transformations which appears in the studies of H. Poincaré on Fuchsian [[#References|[1]]] and Kleinian [[#References|[2]]] groups. The method makes it possible, on one hand, to clarify the structure of a discrete group of transformations as an abstract group (i.e. to find its generators and defining relations) and, on the other hand, to prove the discreteness and to find a fundamental domain of a group of transformations with given generators. The principle of this method is as follows. Let $ \Gamma $ | ||
| + | be a discrete group of isometries of an $ n $- | ||
| + | dimensional simply-connected complete space $ X $ | ||
| + | of constant curvature, and let $ \Phi $ | ||
| + | be a convex polyhedron which is a fundamental domain. The group $ \Gamma $ | ||
| + | is then generated by the set | ||
| − | + | $$ | |
| + | M = \{ {\gamma \in \Gamma } : { \mathop{\rm dim} ( \Phi \cap \gamma ( \Phi ) ) | ||
| + | = n - 1 } \} | ||
| + | . | ||
| + | $$ | ||
| − | All possible relations of the following two types may be taken as defining relations: | + | All possible relations of the following two types may be taken as defining relations: $ \gamma _ {1} \gamma _ {2} = 1 $ |
| + | where $ \gamma _ {1} , \gamma _ {2} \in M $, | ||
| + | and $ \gamma _ {1} \dots \gamma _ {k} = 1 $ | ||
| + | where $ \gamma _ {1} \dots \gamma _ {k} \in M $, | ||
| − | + | $$ | |
| + | \mathop{\rm dim} ( \Phi \cap \gamma _ {1} ( \Phi ) \cap \dots \cap \gamma _ {1} \dots \gamma _ {k-} 1 | ||
| + | ( \Phi ) ) = n - 2 , | ||
| + | $$ | ||
| − | + | $ \gamma _ {i} \gamma _ {i+} 1 \neq 1 $ | |
| + | if $ i = 1 \dots k - 1 $, | ||
| + | and $ \gamma _ {1} \dots \gamma _ {l} \neq 1 $ | ||
| + | if $ l < k $[[#References|[7]]], [[#References|[3]]], [[#References|[6]]]. Conversely, let $ \Phi $ | ||
| + | be a convex polyhedron in an $ n $- | ||
| + | dimensional simply-connected complete space $ X $ | ||
| + | of constant curvature (including the degenerate case in which certain bihedral angles of the polyhedron $ \Phi $ | ||
| + | are equal to $ \pi $), | ||
| + | and let an isometry $ \gamma _ {F} $ | ||
| + | of $ X $ | ||
| + | such that $ \Phi \cap \gamma _ {F} ( \Phi ) = F $ | ||
| + | be given for each $ ( n - 1 ) $- | ||
| + | dimensional face $ F $ | ||
| + | of the polyhedron $ \Phi $. | ||
| + | Also, 1) let there exist a face $ F ^ { \prime } $ | ||
| + | such that $ \gamma _ {F} \gamma _ {F ^ { \prime } } = 1 $ | ||
| + | for each $ ( n - 1 ) $- | ||
| + | dimensional face $ F $ | ||
| + | of $ \Phi $; | ||
| + | and 2) let, for each $ ( n - 2 ) $- | ||
| + | dimensional face $ E $ | ||
| + | of $ \Phi $ | ||
| + | there exist a sequence $ F _ {1} \dots F _ {k} $ | ||
| + | of $ ( n - 1 ) $- | ||
| + | dimensional faces of $ \Phi $ | ||
| + | such that $ \gamma _ {F _ {1} } \dots \gamma _ {F _ {k} } = 1 $, | ||
| − | + | $$ | |
| + | \Phi \cap \gamma _ {F _ {1} } ( \Phi ) \ | ||
| + | \cap \dots \cap \gamma _ {F _ {1} } \dots \gamma _ {F _ {k-} 1 } ( \Phi ) = E , | ||
| + | $$ | ||
| − | and such that the polyhedra | + | and such that the polyhedra $ \Phi $, |
| + | $ \gamma _ {F _ {1} } ( \Phi ) \dots \gamma _ {F _ {1} } \dots \gamma _ {F _ {k-} 1 } ( \Phi ) $ | ||
| + | have pairwise no common interior points. Under these conditions the group of isometries of $ X $ | ||
| + | generated by the transformations $ \gamma _ {F} $ | ||
| + | is discrete and the polyhedron $ \Phi $ | ||
| + | is a fundamental domain. This is a consequence of a more general result obtained by A.D. Aleksandrov [[#References|[4]]] concerning the filling of a space by convex polyhedra (see also [[#References|[8]]]). The following description of freely-acting Fuchsian groups with a compact quotient space, which is due to Poincaré, may serve as an example of the above-said. In this context, the complex upper half-plane $ \mathbf C ^ {+} $ | ||
| + | is taken to be the standard model of the Lobachevskii geometry (Poincaré's model of the Lobachevskii plane). As fundamental domain of any Fuchsian group of the type dealt with here one may take a convex bounded $ 4g $- | ||
| + | gon $ \Phi $ | ||
| + | having the following properties: a) the sum of its interior angles is $ 2 \pi $; | ||
| + | and b) if, for a given direction of traversal of the boundary $ \partial \Phi $ | ||
| + | of the polygon $ \Phi $, | ||
| + | one denotes its sides by $ b _ {1} , b _ {2} $, | ||
| + | $ d _ {1} , d _ {2} $, | ||
| + | $ b _ {3} , b _ {4} $, | ||
| + | $ d _ {3} , d _ {4} \dots b _ {2g-} 1 , b _ {2g} $, | ||
| + | $ d _ {2g-} 1 , d _ {2g} $, | ||
| + | then the length of $ b _ {i} $ | ||
| + | will equal the length of $ d _ {i} $ | ||
| + | for all $ i = 1 \dots 2g $. | ||
| + | The figure shows such a Dirichlet domain for $ g = 3 $. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d033080a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d033080a.gif" /> | ||
| Line 68: | Line 223: | ||
Figure: d033080a | Figure: d033080a | ||
| − | If one now denotes by | + | If one now denotes by $ \gamma _ {i} $, |
| + | $ i = 1 \dots 2g $, | ||
| + | the isometries of the plane $ \mathbf C ^ {+} $ | ||
| + | which preserve orientation and map, with a change of the direction, $ b _ {i} $ | ||
| + | to $ d _ {i} $ | ||
| + | if $ i $ | ||
| + | is even, and $ d _ {i} $ | ||
| + | to $ b _ {i} $ | ||
| + | if $ i $ | ||
| + | is odd (it is assumed that the directions of the sides of $ \Phi $ | ||
| + | are those induced by the direction of traversal of $ \partial \Phi $), | ||
| + | the set $ \{ \gamma _ {1} \dots \gamma _ {2g} \} $ | ||
| + | is a system of generators for $ \Gamma $. | ||
| + | The unique relation between these generators has the form | ||
| − | + | $$ | |
| + | \gamma _ {1} \gamma _ {2} \gamma _ {1} ^ {-} 1 \gamma _ {2} ^ {-} 1 \dots | ||
| + | \gamma _ {2g - 1 } \gamma _ {2g} \gamma _ {2g-} 1 ^ {-} 1 | ||
| + | \gamma _ {2g} ^ {-} 1 = 1 . | ||
| + | $$ | ||
| − | Conversely, if | + | Conversely, if $ \Phi $ |
| + | is an arbitrary convex bounded polygon which satisfies the conditions a) and b), then the group $ \Gamma $ | ||
| + | generated by the isometries $ \gamma _ {1} \dots \gamma _ {2g} $ | ||
| + | is a freely-acting Fuchsian group, while the compact manifold $ \mathbf C ^ {+} / \Gamma $ | ||
| + | is a compact [[Riemann surface|Riemann surface]] of genus $ g $. | ||
| − | The cohomology theory of discrete groups of transformations consists of studying the connection between the cohomology of the space | + | The cohomology theory of discrete groups of transformations consists of studying the connection between the cohomology of the space $ X $, |
| + | of the space $ X / \Gamma $ | ||
| + | and of the group $ \Gamma $. | ||
| + | In particular (Example 4), if $ \Gamma $ | ||
| + | is a discrete group of transformations which is the group of covering transformations of a regular covering $ p : X \rightarrow X / \Gamma $, | ||
| + | where $ X $ | ||
| + | is an acyclic topological space (i.e. $ H _ {n} ( X) = 0 $ | ||
| + | if $ n \geq 1 $ | ||
| + | and $ H _ {0} ( X) = \mathbf Z $), | ||
| + | then the singular cohomology of $ X / \Gamma $ | ||
| + | and the cohomology of $ \Gamma $ | ||
| + | as an abstract group with coefficients in an Abelian group $ A $( | ||
| + | with the trivial structure of a $ \Gamma $- | ||
| + | module) are connected by certain isomorphisms: | ||
| − | + | $$ | |
| + | H ^ {n} ( X / \Gamma , A ) \cong H ^ {n} ( \Gamma , A ) , | ||
| + | \ n = 0 , 1 \dots | ||
| + | $$ | ||
| − | which are natural with respect to | + | which are natural with respect to $ A $[[#References|[10]]]. In the general case the connection between the above cohomology groups is expressed with the aid of certain spectral sequences [[#References|[9]]], [[#References|[10]]]. |
See also [[Automorphic form|Automorphic form]]; [[Automorphic function|Automorphic function]]; [[Arithmetic group|Arithmetic group]]. | See also [[Automorphic form|Automorphic form]]; [[Automorphic function|Automorphic function]]; [[Arithmetic group|Arithmetic group]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Poincaré, "Théorie des groupes fuchsiennes" , ''Oeuvres'' , '''2''' , Gauthier-Villars (1952) pp. 108–168 (Acta Math. | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Poincaré, "Théorie des groupes fuchsiennes" , ''Oeuvres'' , '''2''' , Gauthier-Villars (1952) pp. 108–168 (Acta Math. '''1''' (1982), 1–62)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Poincaré, "Mémoire sur les groupes kleinéens" , ''Oeuvres'' , '''2''' , Gauthier-Villars (1952) pp. 258–299 (Acta Math. '''3''' (1883), 49–92)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M. Gerstenhaber, "On the algebraic structure of discontinuous groups" ''Proc. Amer. Math. Soc.'' , '''4''' (1953) pp. 745–750</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.D. Aleksandrov, "On a completion of a space of polyhedra" ''Vestnik Leningrad. Gos. Univ.'' , '''9''' : 2 (1954) pp. 34–43 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> H.S.M. Coxeter, W.O.J. Moser, "Generators and relations for discrete groups" , Springer (1972)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A. Weil, "Discrete subgroups of Lie groups" ''Ann. of Math.'' , '''72''' (1960) pp. 369–384</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> A.M. Macbeath, "Groups of homeomorphisms of a simply connected space" ''Ann. of Math.'' , '''79''' (1964) pp. 473–488</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> H. Abels, "Geometrische Erzeugung von diskontinuierlichen Gruppen" , Univ. Münster (1966)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A. Grothendieck, "Sur quelques points d'algèbre homologique" ''Tohoku Math. J.'' , '''9''' (1957) pp. 119–221</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> S. MacLane, "Homology" , Springer (1963)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> J. Lehner, "Discontinuous groups and automorphic functions" , Amer. Math. Soc. (1964)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> J.P. Serre, "Cohomogie des groupes discretes" ''C.R. Acad. Sci. Paris'' , '''268''' (1969) pp. 268–271</TD></TR> |
| − | + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> A.F. Baerdon, "The geometry of discrete groups" , Springer (1983)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.A. Wolf, "Spaces of constant curvature" , McGraw-Hill (1967)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Borel, N. Wallach, "Continuous cohomology, discrete subgroups and representations of reductive groups" , Princeton Univ. Press (1980)</TD></TR></table> | |
| − | |||
| − | |||
| − | ==== | ||
| − | |||
| − | + | {{OldImage}} | |
| − | |||
Latest revision as of 11:51, 26 March 2023
A group $ \Gamma $
of homeomorphisms of a Hausdorff space $ X $
that satisfies the following condition: It is possible to find neighbourhoods $ U , V $
of arbitrary points $ x , y \in X $
such that the set
$$ \{ {\gamma \in \Gamma } : {\gamma ( U) \cap V \neq \emptyset } \} $$
is finite. The stabilizer
$$ \Gamma _ {x} = \{ {\gamma \in \Gamma } : {\gamma ( x) = x } \} $$
of a point $ x \in X $ with respect to a discrete group of transformations is finite, while the orbit of an arbitrary point $ x \in X $ is discrete. If $ X $ is a metric space and the transformations from $ \Gamma $ are isometries, these two conditions are sufficient for $ \Gamma $ to be a discrete group of transformations.
Examples.
1) The group of parallel translations of the real plane $ \mathbf R ^ {2} $ over all possible integer vectors:
$$ ( x , y) \rightarrow ( x + n , y + m ) ,\ \ ( x , y) \in \mathbf R ^ {2} ; \ n , m \in \mathbf Z . $$
2) Let $ X $ be the complex upper half-plane
$$ \mathbf C ^ {+} = \{ {z \in \mathbf C } : { \mathop{\rm Im} z > 0 } \} , $$
considered with the ordinary Hausdorff topology, and let $ \Gamma $ be the group of Möbius transformations of the form
$$ z \rightarrow \frac{a z + b }{c z + d } , $$
where $ a $, $ b $, $ c $, and $ d $ are integers and $ ad - bc = 1 $( the Kleinian modular group).
3) Any finite group $ \Gamma $ of homeomorphisms of a Hausdorff space $ X $. (The example of an irreducible algebraic variety with the Zariski topology shows that the condition of separability of $ X $ is essential.)
4) The group of covering transformations of an arbitrary regular covering $ p : X \rightarrow Y $, where $ X $ is connected and locally path-connected, while $ Y $ is a Hausdorff space, is a freely-acting (i.e. $ \Gamma _ {x} = \{ 1 \} $ for any $ x \in X $) discrete group of transformations; the covering $ p $ itself coincides with the mapping of factorization by this group. Conversely, if $ \Gamma $ is a freely-acting discrete group of transformations of a connected topological space $ X $, then the quotient space $ X / \Gamma $ is a Hausdorff space, and the quotient mapping $ p : X \rightarrow X / \Gamma $ is a regular covering of $ X / \Gamma $ with $ \Gamma $ as group of covering transformations. In particular, by virtue of the Poincaré–Koebe uniformization theorem, any Riemann surface, apart from a few trivial exceptions, may be obtained by factorization of the complex upper half-plane $ \mathbf C ^ {+} $ by a freely-acting discrete group of Möbius transformations with real coefficients (a so-called Fuchsian group).
5) In the theory of moduli of Riemann surfaces (and, more generally, of moduli of complex manifolds of some given type), discrete groups of transformations appear as modular groups (cf. Modular group). The simplest such group is discussed in Example 2.
6) Discrete groups of transformations include the crystallographic groups (cf. Crystallographic group). A fairly wide class of discrete groups of transformations, which includes Fuchsian and crystallographic groups, is constituted by discrete subgroups (cf. Discrete subgroup) of topological groups (in particular, of Lie groups), considered as groups of transformations of homogeneous spaces.
A closed subset $ D $ of a topological space $ X $ with a discrete group $ \Gamma $ of transformations is called a fundamental domain of the group $ \Gamma $ if it is the closure of an open subset and if the sets $ \gamma ( D) $ where $ \gamma \in \Gamma $ have pairwise no common interior points and form a locally finite covering of $ X $. For instance, for the group of parallel translations in Example 1, the square
$$ \tag{* } \{ {( x , y ) \in \mathbf R ^ {2} } : {0 \leq x \leq 1 , 0 \leq y \leq 1 } \} $$
may be taken as a fundamental domain; the same purpose will be served by any parallelogram with vertices at integral points which has no integral points inside or on the sides, while in the case of a Kleinian modular group (Example 2) one may take the so-called modular figure
$$ D = \left \{ {z \in \mathbf C ^ {+} } : {- \frac{1}{2} \leq \mathop{\rm Re} z \leq \frac{1}{2} , | z | \geq 1 } \right \} . $$
In many cases a fundamental domain can be constructed. For instance, if $ X $ is a complete Riemannian manifold, if $ \Gamma $ is the discrete group of transformations of $ X $ consisting of the isometries of this space, and if $ x _ {0} \in X $ is some point for which the stabilizer $ \Gamma _ {x _ {0} } $ is trivial, then the Dirichlet domain
$$ D = $$
$$ = \ \{ {x \in X } : {d ( x, x _ {0} ) \leq d ( x , \gamma ( x _ {0} ) ) \textrm{ for all } \textrm{ non\AAh identity transformations } \gamma \in \Gamma } \} $$
may be taken as a fundamental domain. In the above formula $ d ( x , y ) $ denotes the distance between two points $ x $ and $ y $ from $ X $. If $ X $ is a simply-connected complete space of constant curvature, i.e. a sphere, a Euclidean space or a Lobachevskii space, a Dirichlet domain is a convex polyhedron.
The construction of a fundamental domain and the study of its properties furnish important information about the discrete group of transformations. Thus, the quotient space $ X / \Gamma $ is obtained from a fundamental domain by way of "glueing" certain boundary points. For example, the quotient space of the group of parallel translations (Example 1) is obtained from the square (*) by glueing the opposite sides and is homeomorphic to a two-dimensional torus. The concept of a fundamental domain forms the base of the combinatorial-geometric method in the theory of discrete groups of transformations which appears in the studies of H. Poincaré on Fuchsian [1] and Kleinian [2] groups. The method makes it possible, on one hand, to clarify the structure of a discrete group of transformations as an abstract group (i.e. to find its generators and defining relations) and, on the other hand, to prove the discreteness and to find a fundamental domain of a group of transformations with given generators. The principle of this method is as follows. Let $ \Gamma $ be a discrete group of isometries of an $ n $- dimensional simply-connected complete space $ X $ of constant curvature, and let $ \Phi $ be a convex polyhedron which is a fundamental domain. The group $ \Gamma $ is then generated by the set
$$ M = \{ {\gamma \in \Gamma } : { \mathop{\rm dim} ( \Phi \cap \gamma ( \Phi ) ) = n - 1 } \} . $$
All possible relations of the following two types may be taken as defining relations: $ \gamma _ {1} \gamma _ {2} = 1 $ where $ \gamma _ {1} , \gamma _ {2} \in M $, and $ \gamma _ {1} \dots \gamma _ {k} = 1 $ where $ \gamma _ {1} \dots \gamma _ {k} \in M $,
$$ \mathop{\rm dim} ( \Phi \cap \gamma _ {1} ( \Phi ) \cap \dots \cap \gamma _ {1} \dots \gamma _ {k-} 1 ( \Phi ) ) = n - 2 , $$
$ \gamma _ {i} \gamma _ {i+} 1 \neq 1 $ if $ i = 1 \dots k - 1 $, and $ \gamma _ {1} \dots \gamma _ {l} \neq 1 $ if $ l < k $[7], [3], [6]. Conversely, let $ \Phi $ be a convex polyhedron in an $ n $- dimensional simply-connected complete space $ X $ of constant curvature (including the degenerate case in which certain bihedral angles of the polyhedron $ \Phi $ are equal to $ \pi $), and let an isometry $ \gamma _ {F} $ of $ X $ such that $ \Phi \cap \gamma _ {F} ( \Phi ) = F $ be given for each $ ( n - 1 ) $- dimensional face $ F $ of the polyhedron $ \Phi $. Also, 1) let there exist a face $ F ^ { \prime } $ such that $ \gamma _ {F} \gamma _ {F ^ { \prime } } = 1 $ for each $ ( n - 1 ) $- dimensional face $ F $ of $ \Phi $; and 2) let, for each $ ( n - 2 ) $- dimensional face $ E $ of $ \Phi $ there exist a sequence $ F _ {1} \dots F _ {k} $ of $ ( n - 1 ) $- dimensional faces of $ \Phi $ such that $ \gamma _ {F _ {1} } \dots \gamma _ {F _ {k} } = 1 $,
$$ \Phi \cap \gamma _ {F _ {1} } ( \Phi ) \ \cap \dots \cap \gamma _ {F _ {1} } \dots \gamma _ {F _ {k-} 1 } ( \Phi ) = E , $$
and such that the polyhedra $ \Phi $, $ \gamma _ {F _ {1} } ( \Phi ) \dots \gamma _ {F _ {1} } \dots \gamma _ {F _ {k-} 1 } ( \Phi ) $ have pairwise no common interior points. Under these conditions the group of isometries of $ X $ generated by the transformations $ \gamma _ {F} $ is discrete and the polyhedron $ \Phi $ is a fundamental domain. This is a consequence of a more general result obtained by A.D. Aleksandrov [4] concerning the filling of a space by convex polyhedra (see also [8]). The following description of freely-acting Fuchsian groups with a compact quotient space, which is due to Poincaré, may serve as an example of the above-said. In this context, the complex upper half-plane $ \mathbf C ^ {+} $ is taken to be the standard model of the Lobachevskii geometry (Poincaré's model of the Lobachevskii plane). As fundamental domain of any Fuchsian group of the type dealt with here one may take a convex bounded $ 4g $- gon $ \Phi $ having the following properties: a) the sum of its interior angles is $ 2 \pi $; and b) if, for a given direction of traversal of the boundary $ \partial \Phi $ of the polygon $ \Phi $, one denotes its sides by $ b _ {1} , b _ {2} $, $ d _ {1} , d _ {2} $, $ b _ {3} , b _ {4} $, $ d _ {3} , d _ {4} \dots b _ {2g-} 1 , b _ {2g} $, $ d _ {2g-} 1 , d _ {2g} $, then the length of $ b _ {i} $ will equal the length of $ d _ {i} $ for all $ i = 1 \dots 2g $. The figure shows such a Dirichlet domain for $ g = 3 $.
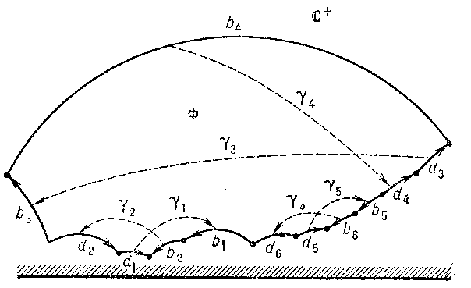
Figure: d033080a
If one now denotes by $ \gamma _ {i} $, $ i = 1 \dots 2g $, the isometries of the plane $ \mathbf C ^ {+} $ which preserve orientation and map, with a change of the direction, $ b _ {i} $ to $ d _ {i} $ if $ i $ is even, and $ d _ {i} $ to $ b _ {i} $ if $ i $ is odd (it is assumed that the directions of the sides of $ \Phi $ are those induced by the direction of traversal of $ \partial \Phi $), the set $ \{ \gamma _ {1} \dots \gamma _ {2g} \} $ is a system of generators for $ \Gamma $. The unique relation between these generators has the form
$$ \gamma _ {1} \gamma _ {2} \gamma _ {1} ^ {-} 1 \gamma _ {2} ^ {-} 1 \dots \gamma _ {2g - 1 } \gamma _ {2g} \gamma _ {2g-} 1 ^ {-} 1 \gamma _ {2g} ^ {-} 1 = 1 . $$
Conversely, if $ \Phi $ is an arbitrary convex bounded polygon which satisfies the conditions a) and b), then the group $ \Gamma $ generated by the isometries $ \gamma _ {1} \dots \gamma _ {2g} $ is a freely-acting Fuchsian group, while the compact manifold $ \mathbf C ^ {+} / \Gamma $ is a compact Riemann surface of genus $ g $.
The cohomology theory of discrete groups of transformations consists of studying the connection between the cohomology of the space $ X $, of the space $ X / \Gamma $ and of the group $ \Gamma $. In particular (Example 4), if $ \Gamma $ is a discrete group of transformations which is the group of covering transformations of a regular covering $ p : X \rightarrow X / \Gamma $, where $ X $ is an acyclic topological space (i.e. $ H _ {n} ( X) = 0 $ if $ n \geq 1 $ and $ H _ {0} ( X) = \mathbf Z $), then the singular cohomology of $ X / \Gamma $ and the cohomology of $ \Gamma $ as an abstract group with coefficients in an Abelian group $ A $( with the trivial structure of a $ \Gamma $- module) are connected by certain isomorphisms:
$$ H ^ {n} ( X / \Gamma , A ) \cong H ^ {n} ( \Gamma , A ) , \ n = 0 , 1 \dots $$
which are natural with respect to $ A $[10]. In the general case the connection between the above cohomology groups is expressed with the aid of certain spectral sequences [9], [10].
See also Automorphic form; Automorphic function; Arithmetic group.
References
| [1] | H. Poincaré, "Théorie des groupes fuchsiennes" , Oeuvres , 2 , Gauthier-Villars (1952) pp. 108–168 (Acta Math. 1 (1982), 1–62) |
| [2] | H. Poincaré, "Mémoire sur les groupes kleinéens" , Oeuvres , 2 , Gauthier-Villars (1952) pp. 258–299 (Acta Math. 3 (1883), 49–92) |
| [3] | M. Gerstenhaber, "On the algebraic structure of discontinuous groups" Proc. Amer. Math. Soc. , 4 (1953) pp. 745–750 |
| [4] | A.D. Aleksandrov, "On a completion of a space of polyhedra" Vestnik Leningrad. Gos. Univ. , 9 : 2 (1954) pp. 34–43 (In Russian) |
| [5] | H.S.M. Coxeter, W.O.J. Moser, "Generators and relations for discrete groups" , Springer (1972) |
| [6] | A. Weil, "Discrete subgroups of Lie groups" Ann. of Math. , 72 (1960) pp. 369–384 |
| [7] | A.M. Macbeath, "Groups of homeomorphisms of a simply connected space" Ann. of Math. , 79 (1964) pp. 473–488 |
| [8] | H. Abels, "Geometrische Erzeugung von diskontinuierlichen Gruppen" , Univ. Münster (1966) |
| [9] | A. Grothendieck, "Sur quelques points d'algèbre homologique" Tohoku Math. J. , 9 (1957) pp. 119–221 |
| [10] | S. MacLane, "Homology" , Springer (1963) |
| [11] | J. Lehner, "Discontinuous groups and automorphic functions" , Amer. Math. Soc. (1964) |
| [12] | J.P. Serre, "Cohomogie des groupes discretes" C.R. Acad. Sci. Paris , 268 (1969) pp. 268–271 |
| [a1] | A.F. Baerdon, "The geometry of discrete groups" , Springer (1983) |
| [a2] | J.A. Wolf, "Spaces of constant curvature" , McGraw-Hill (1967) |
| [a3] | A. Borel, N. Wallach, "Continuous cohomology, discrete subgroups and representations of reductive groups" , Princeton Univ. Press (1980) |
Discrete group of transformations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Discrete_group_of_transformations&oldid=18497