Dini criterion
From Encyclopedia of Mathematics
If a  -periodic function
-periodic function  which is integrable on the segment
which is integrable on the segment  satisfies the condition
satisfies the condition
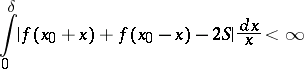 |
at a point  for a fixed number
for a fixed number  ,
,  , and an arbitrary
, and an arbitrary  , then the Fourier series of
, then the Fourier series of  at
at  converges to
converges to  . The criterion was proved by U. Dini [1]. It is a final (sharp) statement in the following sense. If
. The criterion was proved by U. Dini [1]. It is a final (sharp) statement in the following sense. If 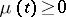 is a continuous function such that the function
is a continuous function such that the function 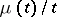 is not integrable in a neighbourhood of the point
is not integrable in a neighbourhood of the point 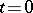 , it is possible to find a continuous function
, it is possible to find a continuous function 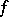 whose Fourier series diverges at
whose Fourier series diverges at 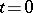 and such that
and such that
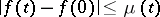 |
for small 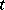 .
.
References
| [1] | U. Dini, "Serie di Fourier e altre rappresentazioni analitiche delle funzioni di una variabile reale" , Pisa (1880) |
| [2] | A. Zygmund, "Trigonometric series" , 1 , Cambridge Univ. Press (1988) |
How to Cite This Entry:
Dini criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dini_criterion&oldid=16762
Dini criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dini_criterion&oldid=16762
This article was adapted from an original article by B.I. Golubov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article