Differential equation, abstract
Either a differential equation in some abstract space (a Hilbert space, a Banach space, etc.) or a differential equation with operator coefficients. The classical abstract differential equation which is most frequently encountered is the equation
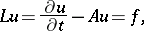 | (1) |
where the unknown function  belongs to some function space
belongs to some function space  ,
,  , and
, and  is an operator (usually a linear operator) acting on this space. If the operator
is an operator (usually a linear operator) acting on this space. If the operator  is a bounded operator or a constant (does not depend on
is a bounded operator or a constant (does not depend on  ), the formula
), the formula
 |
yields the unique solution of equation (1) satisfying the condition  . For a variable operator
. For a variable operator 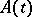 ,
,  is replaced by the evolution operator
is replaced by the evolution operator 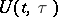 (cf. also Cauchy operator). If the operator
(cf. also Cauchy operator). If the operator  is unbounded, the solutions of the Cauchy problem
is unbounded, the solutions of the Cauchy problem  need not exist for some
need not exist for some  , need not be unique and may break off for
, need not be unique and may break off for 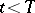 . An exhaustive treatment of the homogeneous (
. An exhaustive treatment of the homogeneous (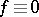 ) equation (1) with a constant operator is given by the theory of semi-groups, while the problems of existence and uniqueness are solved in terms of the resolvent of
) equation (1) with a constant operator is given by the theory of semi-groups, while the problems of existence and uniqueness are solved in terms of the resolvent of  [1], [5]. The same method is also applicable to a variable operator, if it depends smoothly on
[1], [5]. The same method is also applicable to a variable operator, if it depends smoothly on 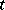 . Another method of study of equation (1), which usually gives less accurate results, but which is applicable to wider classes of equations (even including non-linear equations in some cases), is the use of energy inequalities:
. Another method of study of equation (1), which usually gives less accurate results, but which is applicable to wider classes of equations (even including non-linear equations in some cases), is the use of energy inequalities: 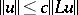 , which are also obtained if certain assumptions are made regarding
, which are also obtained if certain assumptions are made regarding 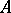 . For a Hilbert space
. For a Hilbert space  one usually postulates different positivity properties of the scalar product
one usually postulates different positivity properties of the scalar product 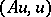 [2]. All the above can be extended, to a certain extent, to more general abstract differential equations
[2]. All the above can be extended, to a certain extent, to more general abstract differential equations
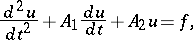 | (2) |
studied under the condition  ,
,  . Very often, the study of equation (2) by various methods (reduction to a set of equations of the first order, a substitution
. Very often, the study of equation (2) by various methods (reduction to a set of equations of the first order, a substitution  , subdivision of the left-hand side into a product of two operators of the first order, etc.) really amounts to the study of equation (1). A principal reason for the existing interest in abstract differential equations is that the so-called mixed problems in cylindrical domains for classical parabolic and hyperbolic equations of the second order can be reduced to equations of the form (1) or (2): The function
, subdivision of the left-hand side into a product of two operators of the first order, etc.) really amounts to the study of equation (1). A principal reason for the existing interest in abstract differential equations is that the so-called mixed problems in cylindrical domains for classical parabolic and hyperbolic equations of the second order can be reduced to equations of the form (1) or (2): The function  is regarded as a function of
is regarded as a function of  with values in the corresponding space of functions in
with values in the corresponding space of functions in  , while the operators
, while the operators  ,
,  are generated by differentiations with respect to
are generated by differentiations with respect to  , subject to the boundary conditions on the side surfaces of the cylinder (the generatrices of which are parallel to the
, subject to the boundary conditions on the side surfaces of the cylinder (the generatrices of which are parallel to the  -axis). Equations (1), (2), in which the postulated properties of the operators
-axis). Equations (1), (2), in which the postulated properties of the operators 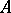 ,
,  coincide with those obtained in the situation described above, are known as parabolic or hyperbolic. Abstract elliptic operators are considered less often.
coincide with those obtained in the situation described above, are known as parabolic or hyperbolic. Abstract elliptic operators are considered less often.
Problems in scattering theory [3] in the interval  are often formulated in terms of semi-groups and equation (1). The reduction of problems in partial differential equations to problems (1) and (2) in abstract differential equations are very convenient in developing approximate (e.g. difference [4]) methods of solution and in the study of asymptotic methods ( "small" and "large" parameters). General abstract differential equations with operator coefficients
are often formulated in terms of semi-groups and equation (1). The reduction of problems in partial differential equations to problems (1) and (2) in abstract differential equations are very convenient in developing approximate (e.g. difference [4]) methods of solution and in the study of asymptotic methods ( "small" and "large" parameters). General abstract differential equations with operator coefficients
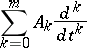 |
and boundary conditions on both ends of the interval  for unbounded operators
for unbounded operators 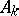 can be meaningfully studied only if very special assumptions concerning
can be meaningfully studied only if very special assumptions concerning  are made. For bounded
are made. For bounded 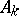 there is no difficulty in extending the theory of ordinary differential equations in an appropriate manner.
there is no difficulty in extending the theory of ordinary differential equations in an appropriate manner.
References
| [1] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) |
| [2] | J.L. Lions, "Equations différentielles operationelles et problèmes aux limites" , Springer (1961) |
| [3] | P.D. Lax, R.S. Philips, "Scattering theory" , Acad. Press (1967) |
| [4] | A.A. Samarskii, "Theorie der Differenzverfahren" , Akad. Verlagsgesell. Geest u. Portig K.-D. (1984) (Translated from Russian) |
| [5] | S.G. Krein, "Linear differential equations in Banach space" , Transl. Math. Monogr. , 29 , Amer. Math. Soc. (1971) (Translated from Russian) |
Comments
For elliptic problems see [a3].
References
| [a1] | H. Tanabe, "Equations of evolution" , Pitman (1979) (Translated from Japanese) |
| [a2] | A. Pazy, "Semigroups of linear operators and applications to partial differential equations" , Springer (1983) |
| [a3] | S. Agmon, "Unicité convexité dans problèmes différentiels" , Univ. Montréal (1966) |
Differential equation, abstract. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_equation,_abstract&oldid=14482