Differentiability of solutions (of differential equations)
A property of solutions of differential equations, viz. that the solutions posses a specific number of continuous derivatives with respect to the independent variable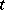 
and the parameter 
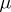appearing in the equation. In the theory of differential equations the problem is posed as follows: What are the properties which the right-hand side of the equation must have for the solution to have a given number of continuous derivatives with respect to 
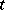and 
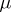? This problem has been most thoroughly investigated for ordinary differential equations [1], [4].
Consider an equation of the type (
may also be a vector):
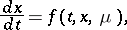 | (1) |
where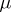 
is a parameter (usually also a vector), and let 
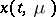be a solution of (1) defined by the initial condition
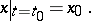 | (2) |
First differentiability of the solution with respect to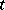 
is considered. If 
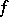is continuous with respect to 
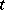and 
, the theorem on the existence of a continuous solution of the problem (1)–(2) is applicable in some domain, and then it follows from the identity which is obtained after substitution of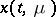 
in (1) that the continuous derivative 
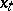also exists. The presence of 
continuous derivatives of 
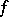with respect to 
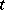and 
means that there exist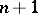 
continuous derivatives of the solution with respect to 
; 
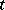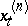may be found (expressed in terms of 
) by successive differentiation of the identity obtained by substituting 
in (1).
In several problems, e.g. in constructing the asymptotics of the solution in the parameter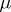 
, it is necessary to study derivatives of 
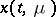with respect to 
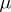. In order to be specific, the existence of derivatives with respect to 
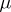for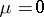 
will be considered. If 
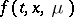is continuous and has continuous partial derivatives with respect to 
and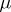 
in some domain, 
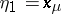exists and is defined from the so-called variational equation (equation in variations, which is linear in 
), obtained from (1) by differentiating both parts with respect to 
and putting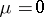 
:
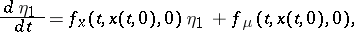 | (3) |
and with the aid of the initial condition
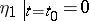 | (4) |
if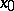 
is independent of 
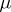; if, however, 
, then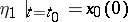 
.
The derivative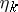 
of 
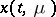with respect to 
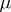of order 
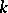(under the condition that 
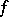has continuous partial derivatives up to order 
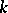) is defined by the variational equation of the 
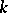-th order, which differs from (3) only in its inhomogeneity, and it depends on 
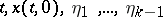. In the presence of 
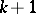continuous derivatives of 
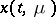with respect to 
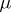, Taylor's formula may be used as the asymptotic formula for 
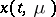with respect to 
:
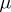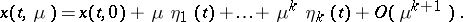 | (5) |
This is very important, since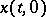 
and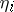 
can then be found from equations simpler than (1).
If the right-hand side depends analytically on its arguments, the solution is an analytic function of the parameter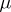 
(see, for example, [2]).
The problem of differentiability of solutions with respect to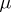 
is still meaningful in several cases when the right-hand side does not depend regularly on 
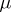. In one such case 
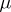appears as the coefficient in front of the derivative:
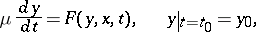 | (6) |
 |
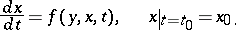If (6) is rewritten in the form (1), i.e. is solved with respect to the derivatives, a pole-type singularity appears on the right-hand side as 
. It is found that, in the presence of 
continuous derivatives of the right-hand sides and under certain special conditions (the so-called stability conditions), expansion (5) is valid, where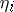 
are the limit values of the derivatives with respect to 
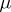of the solution of (6) as 
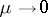, which are defined by the variational equation constructed according to the same rule: (6) is differentiated with respect to 
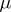and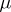 
is set equal to zero. However, as distinct from the regular case, the system of variational equations will be of a lower order than (6), and the initial values for 
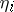will no longer be zero — but will be equal to (usually non-zero) constants, obtained by a definite rule [3].
References
| [1] | I.G. Petrovskii, "Ordinary differential equations" , Prentice-Hall (1966) (Translated from Russian) |
| [2] | A.N. Tikhonov, "On the dependence of solutions of differential equations on a small parameter" Mat. Sb. , 22 : 2 (1948) pp. 193–204 (In Russian) |
| [3] | A.B. Vasil'eva, V.F. Butuzov, "Asymptotic expansions of solutions of singularly perturbed equations" , Moscow (1973) (In Russian) |
| [4] | A.N. Tikhonov, A.B. Vasil'eva, A.G. Sveshnikov, "Differential equations" , Springer (1985) (Translated from Russian) |
Comments
References
| [a1] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17 |
| [a2] | D.R. Smith, "Singular perturbation theory" , Cambridge Univ. Press (1985) |
Differentiability of solutions (of differential equations). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differentiability_of_solutions_(of_differential_equations)&oldid=15901