Diagram geometry
A diagram is like a blueprint describing a possible combination of  -dimensional incidence structures in a higher-dimensional geometry (cf. Incidence system). In this context, a geometry of rank
-dimensional incidence structures in a higher-dimensional geometry (cf. Incidence system). In this context, a geometry of rank  is a connected graph
is a connected graph  equipped with an
equipped with an  -partition
-partition  such that every maximal clique of
such that every maximal clique of  meets every class of
meets every class of  . The vertices and the adjacency relation of
. The vertices and the adjacency relation of  are the elements and the incidence relation of the geometry, the cliques of
are the elements and the incidence relation of the geometry, the cliques of  are called flags, the neighbourhood of a non-maximal flag is its residue, the classes of
are called flags, the neighbourhood of a non-maximal flag is its residue, the classes of  are called types and the type (respectively, rank) of a residue is the set (respectively, number) of types met by it. Given a catalogue of "nice" geometries of rank
are called types and the type (respectively, rank) of a residue is the set (respectively, number) of types met by it. Given a catalogue of "nice" geometries of rank  and a symbol for each of those classes, one can compose diagrams of any rank by those symbols. The nodes of a diagram represent types and, by attaching a label to the stroke connecting two types
and a symbol for each of those classes, one can compose diagrams of any rank by those symbols. The nodes of a diagram represent types and, by attaching a label to the stroke connecting two types 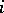 and
and  or by some other convention, one indicates which class the residues of type
or by some other convention, one indicates which class the residues of type  should belong to. For instance, a simple stroke
should belong to. For instance, a simple stroke
a double stroke
and the "null stroke"
are normally used to denote, respectively, the class of projective planes (cf. Projective plane), the class of generalized quadrangles [a5] (cf. also Quadrangle) and the class of generalized digons (generalized digons are the trivial geometry of rank  , where any two elements of different type are incident). The following two diagrams are drawn according to these conventions.
, where any two elements of different type are incident). The following two diagrams are drawn according to these conventions.
1)
2)
They both represent geometries of rank  , where the residues of type
, where the residues of type 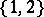 are projective planes and the residues of type
are projective planes and the residues of type 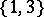 are generalized digons. However, the residues of type
are generalized digons. However, the residues of type  are projective planes in 1) and generalized quadrangles in 2). The following is a typical problem in diagram geometry: given a diagram of such-and-such type, classify the geometries that fit with it, or at least the finite or flag-transitive such geometries (a geometry
are projective planes in 1) and generalized quadrangles in 2). The following is a typical problem in diagram geometry: given a diagram of such-and-such type, classify the geometries that fit with it, or at least the finite or flag-transitive such geometries (a geometry 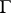 is said to be flag-transitive if
is said to be flag-transitive if 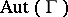 acts transitively on the set of maximal flags of
acts transitively on the set of maximal flags of 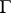 ). In the "best" cases the answer is as follows: the geometries under consideration belong to a certain well-known family or, possibly, arise in connection with certain small or sporadic groups. For instance, it is not difficult to prove that
). In the "best" cases the answer is as follows: the geometries under consideration belong to a certain well-known family or, possibly, arise in connection with certain small or sporadic groups. For instance, it is not difficult to prove that  -dimensional projective geometries are the only examples for the above diagram 1). On the other hand, the following has been proved quite recently [a7]: If
-dimensional projective geometries are the only examples for the above diagram 1). On the other hand, the following has been proved quite recently [a7]: If 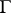 is a flag-transitive example for the diagram 2) and if all rank-
is a flag-transitive example for the diagram 2) and if all rank- residues of
residues of 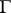 are finite of size
are finite of size  , then
, then 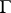 is either a classical polar space [a6] (arising from a non-degenerate alternating, quadratic or Hermitian form of Witt index
is either a classical polar space [a6] (arising from a non-degenerate alternating, quadratic or Hermitian form of Witt index  ) or a uniquely determined very small geometry with
) or a uniquely determined very small geometry with  .
.
See [a3] for a survey of related theorems.
References
| [a1] | F. Buekenhout, "Diagrams for geometries and groups" J. Combin. Th. A , 27 (1979) pp. 121–151 |
| [a2] | F. Buekenhout, "Foundations of incidence geometry" F. Buekenhout (ed.) , Handbook of Incidence Geometry , North-Holland (1995) pp. 63–105 |
| [a3] | F. Buekenhout, A. Pasini, "Finite diagram geometries extending buildings" F. Buekenhout (ed.) , Handbook of Incidence Geometry , North-Holland (1995) pp. 1143–1254 |
| [a4] | A. Pasini, "Diagram geometries" , Oxford Univ. Press (1994) |
| [a5] | S.E. Payne, J.A. Thas, "Finite generalized quadrangles" , Pitman (1984) |
| [a6] | J. Tits, "Buildings of spherical type and finite BN-pairs" , Lecture Notes in Mathematics , 386 , Springer (1974) |
| [a7] | S. Yoshiara, "The flag-transitive  geometries of finite order" J. Algebraic Combinatorics (??) geometries of finite order" J. Algebraic Combinatorics (??) |
Diagram geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Diagram_geometry&oldid=12876