Dehn invariant
An invariant of polyhedra in three-dimensional space that decides whether two polyhedra of the same volume are "scissors congruent" (see Equal content and equal shape, figures of; Hilbert problems; Polyhedron).
Quite generally, a scissors-congruence invariant assigns to a polytope  in space an element
in space an element  in a group such that
in a group such that  ,
,  if
if  is degenerate, and
is degenerate, and  if there is a motion
if there is a motion  of the space such that
of the space such that  .
.
For the Dehn invariant, the group chosen is the tensor product  . To a polytope
. To a polytope 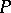 with edges
with edges  one associates the element
one associates the element  , where
, where  is the length of
is the length of 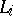 and
and  is the dihedral angle of the planes meeting at
is the dihedral angle of the planes meeting at  . The Sydler theorem states that two polytopes in three-dimensional space are scissors equivalent if and only if they have equal volume and the same Dehn invariant, thus solving Hilbert's third problem in a very precise manner (cf. also Hilbert problems).
. The Sydler theorem states that two polytopes in three-dimensional space are scissors equivalent if and only if they have equal volume and the same Dehn invariant, thus solving Hilbert's third problem in a very precise manner (cf. also Hilbert problems).
For higher dimensions there is a generalization, called the Hadwiger invariant or Dehn–Hadwiger invariant. This has given results in dimension four, [a4], and for the case when the group consists of translations only, [a2].
References
| [a1] | P. Cartier, "Decomposition des polyèdres: le point sur le troisième problème de Hilbert" Sem. Bourbaki , 1984/5 (1986) pp. 261–288 |
| [a2] | C.H. Sah, "Hilbert's third problem: scissors congruence" , Pitman (1979) |
| [a3] | V.G. Boltianskii, "Hilbert's third problem" , Wiley (1978) |
| [a4] | B. Jessen, "Zur Algebra der Polytope" Göttinger Nachrichte Math. Phys. (1972) pp. 47–53 |
Dehn invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dehn_invariant&oldid=35803