Degenerate elliptic equation
A partial differential equation
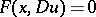 | (1) |
where the real-valued function 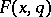 satisfies the condition
satisfies the condition
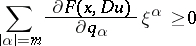 | (2) |
for all real 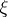 , and there exists a
, and there exists a 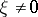 for which (2) becomes an equality. Here,
for which (2) becomes an equality. Here,  is an
is an  -dimensional vector
-dimensional vector 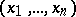 ;
;  is the unknown function;
is the unknown function; 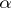 is a multi-index
is a multi-index 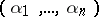 ;
; 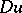 is a vector with components
is a vector with components
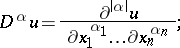 |
the derivatives in equation (1) are of an order not exceeding 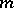 ; the
; the 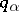 are the components of a vector
are the components of a vector 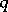 ;
; 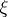 is an
is an  -dimensional vector
-dimensional vector 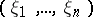 ; and
; and 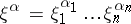 . If strict inequality in equation (2) holds for all
. If strict inequality in equation (2) holds for all  and
and 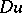 and for all real
and for all real 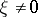 , equation (1) is elliptic at
, equation (1) is elliptic at 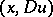 . Equation (1) degenerates at the points
. Equation (1) degenerates at the points 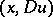 at which inequality (2) becomes an equality for any real
at which inequality (2) becomes an equality for any real 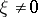 . If equality holds only on the boundary of the domain under consideration, the equation is called degenerate on the boundary of the domain. The most thoroughly studied equations are second-order degenerate elliptic equations
. If equality holds only on the boundary of the domain under consideration, the equation is called degenerate on the boundary of the domain. The most thoroughly studied equations are second-order degenerate elliptic equations
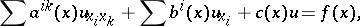 |
where the matrix 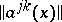 is non-negative definite for all
is non-negative definite for all  -values under consideration.
-values under consideration.
See also Degenerate partial differential equation and the references given there.
Degenerate elliptic equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degenerate_elliptic_equation&oldid=25859