Decimal fraction
An arithmetical fraction with an integral power of 10 as its denominator. The following notation has been accepted for a decimal fraction:
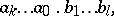 | (1) |
where 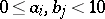 are integers and if
are integers and if  then
then  is also non-zero.
is also non-zero.
Formula (1) expresses the number
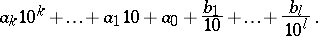 |
For example,
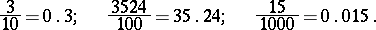 |
The digits to the right of the decimal point are known as the decimal digits. If a decimal fraction contains no integer part, i.e. its absolute value is smaller than one, a zero is placed to the left of the decimal point.
An infinite decimal fraction is an infinite sequence of digits such as
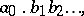 | (2) |
where  is an integer, while each one of the numbers
is an integer, while each one of the numbers  ,
, 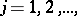 assumes one of the values
assumes one of the values 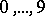 . Any real number
. Any real number 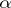 is the sum of such a series, i.e.
is the sum of such a series, i.e.
 |
The partial sums of the series (2) are finite decimal fractions 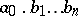 , which are approximate values of the number
, which are approximate values of the number 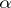 smaller than
smaller than 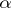 ; the numbers
; the numbers
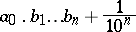 |
are the respective approximate values larger than 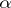 . If there exists integers
. If there exists integers  and
and 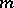 such that for all
such that for all 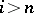 the equalities
the equalities
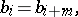 |
are valid, the infinite decimal fraction is said to be periodic. Any finite decimal fraction may be regarded as an infinite periodic fraction with 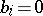 for
for  . If
. If 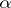 is a rational number, the corresponding fraction (2) will be periodic. If
is a rational number, the corresponding fraction (2) will be periodic. If 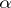 is irrational, the fraction (2) cannot be periodic.
is irrational, the fraction (2) cannot be periodic.
Decimal fraction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Decimal_fraction&oldid=16491