De Rham theorem
A theorem expressing the real cohomology groups of a differentiable manifold  in terms of the complex of differential forms (cf. Differential form) on
in terms of the complex of differential forms (cf. Differential form) on  . If
. If  is the de Rham complex of
is the de Rham complex of  , where
, where  is the space of all infinitely-differentiable
is the space of all infinitely-differentiable  -forms on
-forms on  equipped with the exterior differentiation, then de Rham's theorem establishes an isomorphism between the graded cohomology algebra
equipped with the exterior differentiation, then de Rham's theorem establishes an isomorphism between the graded cohomology algebra  of the complex
of the complex  and the cohomology algebra
and the cohomology algebra  of
of  with values in
with values in  . An explicit interpretation of this isomorphism is that to each closed
. An explicit interpretation of this isomorphism is that to each closed  -form
-form 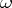 there is associated a linear form
there is associated a linear form  on the space of
on the space of  -dimensional singular cycles
-dimensional singular cycles  in
in  .
.
The theorem was first established by G. de Rham [1], although the idea of a connection between cohomology and differential forms goes back to H. Poincaré.
There are various versions of de Rham's theorem. For example, the cohomology algebra 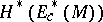 of the complex
of the complex  of forms with compact supports is isomorphic to the real cohomology algebra
of forms with compact supports is isomorphic to the real cohomology algebra  of the manifold
of the manifold  with compact supports. The cohomology of
with compact supports. The cohomology of  with values in a locally constant sheaf of vector spaces is isomorphic to the cohomology of the complex of differential forms with values in the corresponding flat vector bundle [3]. The cohomology of a simplicial set
with values in a locally constant sheaf of vector spaces is isomorphic to the cohomology of the complex of differential forms with values in the corresponding flat vector bundle [3]. The cohomology of a simplicial set  with values in any field
with values in any field  of characteristic 0 is isomorphic to the cohomology of the corresponding de Rham polynomial complex over
of characteristic 0 is isomorphic to the cohomology of the corresponding de Rham polynomial complex over 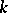 . In the case when
. In the case when  is the singular complex of an arbitrary topological space
is the singular complex of an arbitrary topological space  one obtains in this way a graded-commutative differential graded
one obtains in this way a graded-commutative differential graded  -algebra
-algebra 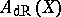 with cohomology algebra
with cohomology algebra 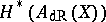 isomorphic to the singular cohomology algebra
isomorphic to the singular cohomology algebra 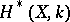 (see [4]). If
(see [4]). If  is a smooth affine algebraic variety over
is a smooth affine algebraic variety over 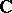 , then the cohomology algebra
, then the cohomology algebra 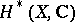 is isomorphic to the cohomology algebra of the complex of regular differential forms on
is isomorphic to the cohomology algebra of the complex of regular differential forms on  (see de Rham cohomology).
(see de Rham cohomology).
References
| [1] | G. de Rham, "Sur l'analysis situs des variétés à  dimensions" J. Math. Pures Appl. Sér. 9 , 10 (1931) pp. 115–200 dimensions" J. Math. Pures Appl. Sér. 9 , 10 (1931) pp. 115–200 |
| [2] | G. de Rham, "Differentiable manifolds" , Springer (1984) (Translated from French) |
| [3] | M.S. Raghunathan, "Discrete subgroups of Lie groups" , Springer (1972) |
| [4] | D. Lehmann, "Théorie homotopique des forms différentiélles (d'après D. Sullivan)" Astérisque , 45 (1977) |
De Rham theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_Rham_theorem&oldid=13456