De Moivre formula
From Encyclopedia of Mathematics
The formula expressing the rule for raising a complex number, expressed in trigonometric form
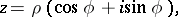 |
to an  -th power. According to de Moivre's formula the modulus
-th power. According to de Moivre's formula the modulus  of the complex number is raised to that power and the argument
of the complex number is raised to that power and the argument  is multiplied by the exponent:
is multiplied by the exponent:
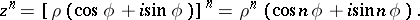 |
The formula was found by A. de Moivre (1707), its modern notation was suggested by L. Euler (1748).
De Moivre's formula can be used to express  and
and  in powers of
in powers of  and
and  :
:
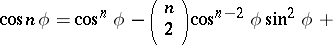 |
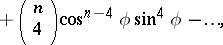 |
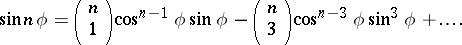 |
Inversion of de Moivre's formula leads to a formula for extracting roots of a complex number:
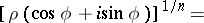 |
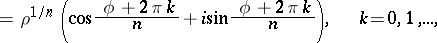 |
which is also sometimes called de Moivre's formula.
Comments
References
| [a1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
How to Cite This Entry:
De Moivre formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_Moivre_formula&oldid=14287
De Moivre formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_Moivre_formula&oldid=14287
This article was adapted from an original article by BSE-3 (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article