Cyclic coordinates
Generalized coordinates of a certain physical system that do not occur explicitly in the expression of the characteristic function of this system. When one uses the corresponding equations of motion, one may obtain at once for every cyclic coordinate the integral of motion corresponding to it. For example, if the Lagrange function 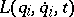 , where the
, where the 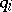 are generalized coordinates, the
are generalized coordinates, the 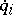 generalized velocities, and
generalized velocities, and 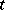 the time, does not contain
the time, does not contain 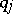 explicitly, then
explicitly, then 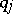 is a cyclic coordinate, and the
is a cyclic coordinate, and the 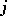 -th Lagrange equation has the form
-th Lagrange equation has the form 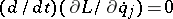 (cf. Lagrange equations (in mechanics)), which at once gives an integral of motion
(cf. Lagrange equations (in mechanics)), which at once gives an integral of motion
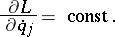 |
References
| [1] | L.D. Landau, E.M. Lifshits, "Mechanics" , Pergamon (1965) (Translated from Russian) |
Comments
The notion of a cyclic coordinate (angle coordinate, angle variable) ties in with action-angle coordinates in the theory of completely-integrable Hamiltonian systems. Each such system (with finite degrees of freedom) can be transformed into one with coordinates  such that the Hamiltonian has the form
such that the Hamiltonian has the form 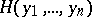 , i.e. does not contain
, i.e. does not contain  . Then the
. Then the 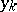 are called the action coordinates and the
are called the action coordinates and the 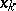 the angle coordinates.
the angle coordinates.
Cyclic coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cyclic_coordinates&oldid=13639