Curve of pursuit
A curve representing a solution of the "pursuit" problem, which is posed as follows: Let a point  be moved uniformly along a given curve. The trajectory has to be found of the uniform movement of a point
be moved uniformly along a given curve. The trajectory has to be found of the uniform movement of a point  , such that the tangent drawn towards the trajectory at any moment of the movement would pass through the position of
, such that the tangent drawn towards the trajectory at any moment of the movement would pass through the position of  corresponding to that moment in time.
corresponding to that moment in time.

Figure: c027400a
In a plane, the system of equations which the curve of pursuit must satisfy takes the form
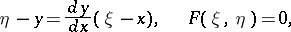 |
where  is the slope of the curve of pursuit, and
is the slope of the curve of pursuit, and  is the equation of the given curve.
is the equation of the given curve.
The "pursuit" problem was posed by Leonardo da Vinci and solved by P. Bouguer (1732). For a generalization of it see the last Chapter of [2].
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [2] | J.E. Littlewood, "A mathematician's miscellany" , Methuen (1953) |
Curve of pursuit. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Curve_of_pursuit&oldid=15061