Curvature form
From Encyclopedia of Mathematics
A  -form
-form  on a principal fibre bundle
on a principal fibre bundle 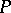 with structure Lie group
with structure Lie group 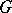 , taking values in the Lie algebra
, taking values in the Lie algebra 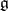 of the group
of the group 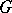 and defined by the connection form
and defined by the connection form  on
on 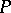 by the formula
by the formula
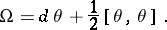 |
The curvature form is a measure of the deviation of the given connection from the locally flat connection characterized by the condition 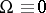 . It satisfies the Bianchi identity
. It satisfies the Bianchi identity
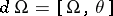 |
and defines the holonomy algebra (see Holonomy group).
Comments
The equation 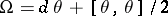 is called the structure equation.
is called the structure equation.
References
| [a1] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1 , Interscience (1963) pp. Chapt. V, VI |
How to Cite This Entry:
Curvature form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Curvature_form&oldid=16422
Curvature form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Curvature_form&oldid=16422
This article was adapted from an original article by Ü. Lumiste (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article