Cremona group
The group  of birational automorphisms of a projective space
of birational automorphisms of a projective space  over a field
over a field  ; or, equivalently, the group of Cremona transformations (cf. Cremona transformation) of
; or, equivalently, the group of Cremona transformations (cf. Cremona transformation) of  .
.
The group  of projective transformations of
of projective transformations of  is contained in a natural manner in
is contained in a natural manner in  as a subgroup; when
as a subgroup; when  it is a proper subgroup. The group
it is a proper subgroup. The group  is isomorphic to the group
is isomorphic to the group  of automorphisms over
of automorphisms over  of the field of rational functions in
of the field of rational functions in  variables over
variables over 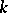 . The fundamental result concerning the Cremona group for the projective plane is Noether's theorem: The group
. The fundamental result concerning the Cremona group for the projective plane is Noether's theorem: The group  over an algebraically closed field is generated by the quadratic transformations or, equivalently, by the standard quadratic transformation and the projective transformations (see [1], [7]); relations between these generators can be found in
over an algebraically closed field is generated by the quadratic transformations or, equivalently, by the standard quadratic transformation and the projective transformations (see [1], [7]); relations between these generators can be found in
(see also ). It is not known to date (1987) whether the Cremona group is simple. There is a generalization of Noether's theorem to the case in which the ground field  is not algebraically closed (see [6]).
is not algebraically closed (see [6]).
One of the most difficult problems in birational geometry is that of describing the structure of the group  , which is no longer generated by the quadratic transformations. Almost all literature on Cremona transformations of three-dimensional space is devoted to concrete examples of such transformations. Finally, practically nothing is known about the structure of the Cremona group for spaces of dimension higher than 3.
, which is no longer generated by the quadratic transformations. Almost all literature on Cremona transformations of three-dimensional space is devoted to concrete examples of such transformations. Finally, practically nothing is known about the structure of the Cremona group for spaces of dimension higher than 3.
An important direction of research in the theory of Cremona groups is the investigation of subgroups of  . The finite subgroups of
. The finite subgroups of  , with
, with  algebraically closed, have been described up to conjugacy (see [8], and also [6]). A classification of all involutions in
algebraically closed, have been described up to conjugacy (see [8], and also [6]). A classification of all involutions in 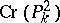 was obtained as far back as 1877 by E. Bertini (see e.g. [4], [5]). The question of describing all involutions in
was obtained as far back as 1877 by E. Bertini (see e.g. [4], [5]). The question of describing all involutions in  ,
,  , remains open. All maximal connected algebraic subgroups in
, remains open. All maximal connected algebraic subgroups in  were described by F. Enriques in 1893 (see [4]): They are just the automorphism groups of all minimal models of rational surfaces, i.e. of the plane
were described by F. Enriques in 1893 (see [4]): They are just the automorphism groups of all minimal models of rational surfaces, i.e. of the plane  , the quadric
, the quadric  and of the series of ruled surfaces
and of the series of ruled surfaces  ,
, 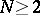 . There are a few generalizations of this result (see [3], [9]) to the case of the group
. There are a few generalizations of this result (see [3], [9]) to the case of the group  ,
,  .
.
References
| [1] | "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) |
| [2] | A.B. Coble, "Algebraic geometry and theta functions" , Amer. Math. Soc. (1929) |
| [3] | M. Demazure, "Sous-groupes algébriques de rang maximum du groupes de Cremona" Ann. Sci. Ecole Norm. Sup. Sér. 4 , 3 : 4 (1970) pp. 507–588 |
| [4] | L. Godeaux, "Les transformations birationelles du plan" , Gauthier-Villars (1927) |
| [5] | H.P. Hudson, "Cremona transformations in plane and space" , Cambridge Univ. Press (1927) |
| [6] | Yu.I. Manin, "Rational surfaces over perfect fields II" Math. USSR-Sb. , 1 (1967) pp. 141–168 Mat. Sb. , 72 : 2 (1967) pp. 161–192 |
| [7] | M. Nagata, "On rational surfaces II" Mem. Coll. Sci. Univ. Kyoto , 33 (1960) pp. 271–293 |
| [8] | A. Wiman, "Zur Theorie der endlichen Gruppen von birationalen Transformationen in der Ebene" Math. Ann. , 48 (1897) pp. 195–240 |
| [9] | H. Umemura, "Sur les sous-groupes algébriques primitifs du groupe de Cremona à trois variables" Nagoya Math. J. , 79 (1980) pp. 47–67 |
Cremona group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cremona_group&oldid=17476