Difference between revisions of "Cox regression model"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 69 formulas out of 74 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 74 formulas, 69 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
A regression model introduced by D.R. Cox [[#References|[a4]]] and subsequently proved to be one of the most useful and versatile statistical models, in particular with regards to applications in survival analysis (cf. also [[Regression analysis|Regression analysis]]). | A regression model introduced by D.R. Cox [[#References|[a4]]] and subsequently proved to be one of the most useful and versatile statistical models, in particular with regards to applications in survival analysis (cf. also [[Regression analysis|Regression analysis]]). | ||
| − | Let | + | Let $X _ { 1 } , \ldots , X _ { n }$ be stochastically independent, strictly positive random variables (cf. also [[Random variable|Random variable]]), to be thought of as the failure times of $n$ different items, such that $X _ { k }$ has hazard function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130250/c1302504.png"/> (i.e. |
| − | + | \begin{equation*} \mathsf{P} ( X _ { k } > t ) = \operatorname { exp } \left( - \int _ { 0 } ^ { t } u _ { k } ( s ) d s \right) \end{equation*} | |
| − | for | + | for $t \geq 0$) of the form |
| − | + | \begin{equation*} u _ { k } ( t ) = \alpha ( t ) e ^ { z _ { k } ^ { T } ( t ) \beta }. \end{equation*} | |
| − | Here, | + | Here, $\alpha$ is an unknown hazard function, the baseline hazard obtained if $\beta = 0$, and $\beta ^ { T } = ( \beta _ { 1 } , \dots , \beta _ { p } )$ is a vector of $p$ unknown regression parameters. The $z _ { k } ^ { T } ( t ) = ( z _ { k , 1 } ( t ) , \dots , z _ { k , p } ( t ) )$ denote known non-random vectors of possibly time-dependent covariates, e.g. individual characteristics of a patient referring to age, sex, method of treatment as well as physiological and other measurements. |
| − | The parameter vector | + | The parameter vector $\beta$ is estimated by maximizing the partial likelihood [[#References|[a5]]] |
| − | + | \begin{equation} \tag{a1} C ( \beta ) = \prod _ { j = 1 } ^ { n } \frac { \operatorname { exp } ( z _ { j } ^ { T } ( T _ { j } ) \beta ) } { \sum _ { k \in R _ { j } } \operatorname { exp } ( z _ { k } ^ { T } ( T _ { j } ) \beta ) }, \end{equation} | |
| − | where | + | where $T _ { 1 } < \ldots < T _ { n }$ are the $X _ { k }$ ordered according to size, $Y _ { j } = i$ if it is item $i$ that fails at time $T _ { j }$, and $R _ { j } = \{ k : X _ { k } \geq T _ { j } \}$ denotes the set of items $k$ still at risk, i.e. not yet failed, immediately before $T _ { j }$. With this setup, the $j$th factor in $C ( \beta )$ describes the [[Conditional distribution|conditional distribution]] of $Y_{j}$ given $T _ { 1 } , \dots , T _ { j }$ and $Y _ { 1 } , \dots , Y _ { j - 1 }$. |
| − | For many applications it is natural to allow for, e.g., censorings (cf. also [[Errors, theory of|Errors, theory of]]) or truncations (the removal of an item from observation through other causes than failure) as well as random covariate processes | + | For many applications it is natural to allow for, e.g., censorings (cf. also [[Errors, theory of|Errors, theory of]]) or truncations (the removal of an item from observation through other causes than failure) as well as random covariate processes $Z _ { k } ( t )$. Formally this may be done by introducing the counting processes $N _ { k } ( t ) = 1 _ { ( X _ { k } \leq t ,\, I _ { k } ( X _ { k } ) = 1 ) }$ registering the failures if they are observed, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130250/c13025030.png"/> is a $0 - 1$-valued [[Stochastic process|stochastic process]] with $I _ { k } ( t ) = 1$ if item $k$ is at risk (under observation) just before time $t$. If $\mathcal{F} _ { t }$ denotes the $\sigma$-algebra for everything observed (failures, censorings, covariate values, etc.) on the time interval $[ 0 , t ]$, it is then required that $N _ { k }$ have $\mathcal{F} _ { t }$-intensity process |
| − | + | \begin{equation} \tag{a2} \lambda _ { k } ( t ) = \alpha ( t ) e ^ { Z _ { k } ^ { T } ( t ) \beta } I _ { k } ( t ), \end{equation} | |
| − | i.e. | + | i.e. $N _ { k } ( t ) - \int _ { 0 } ^ { t } \lambda _ { k } ( s ) d s$ defines a $\mathcal{F} _ { t }$-martingale (cf. also [[Martingale|Martingale]]), while intuitively, for small $h > 0$, the conditional probability given the past that item $k$ will fail during the interval $] t , t + h ]$ is approximately $h \alpha ( t ) e ^ { Z _ { k } ^ { T } ( t ) \beta }$, provided $k$ is at risk at time $t$. For $\beta$ known, (a2) is then an example of Aalen's multiplicative intensity model [[#References|[a1]]] with the integrated baseline hazard $A ( t ) = \int _ { 0 } ^ { t } \alpha ( s ) d s$ estimated by, for any $t$, |
| − | + | \begin{equation} \tag{a3} \hat { A } ( t | \beta ) = \int _ { ]0 , t] } \frac { 1 } { \sum _ { k = 1 } ^ { n } I _ { k } ( s - ) e ^ { Z _ { k } ^ { T } ( s - ) \beta } } d \overline { N } ( s ), \end{equation} | |
| − | writing | + | writing $\overline { N } = \sum _ { k } N _ { k }$ and where $s-$ signifies that it is the values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130250/c13025055.png"/> and $Z _ { k }$ just before the observed failure times that should be used. Since in practice $\beta$ is unknown, in (a3) one of course has to replace $\beta$ by the estimator $\widehat { \beta }$, still obtained maximizing the partial likelihood (a1), replacing $n$ by the random number of observed failures, replacing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130250/c13025061.png"/> by $Z _ { k }$, and using $R _ { j } = \{ k : I _ { k } ( T _ { j } - ) = 1 \}$ with $T _ { j }$ now the $j$th observed failure. (Note that in contrast to the situation with non-random covariates described above, there is no longer an interpretation of the factors in $C ( \beta )$ as conditional distributions.) |
| − | Using central limit theorems for martingales (cf. also [[Central limit theorem|Central limit theorem]]: [[Martingale|Martingale]]), conditions may be given for consistency and asymptotic normality of the estimators | + | Using central limit theorems for martingales (cf. also [[Central limit theorem|Central limit theorem]]: [[Martingale|Martingale]]), conditions may be given for consistency and asymptotic normality of the estimators $\widehat { \beta }$ and $\widehat { A } ( t | \widehat { \beta } )$, see [[#References|[a3]]]. |
| − | It is of particular interest to be able to test for the effect of one or more covariates, i.e. to test hypothesis of the form | + | It is of particular interest to be able to test for the effect of one or more covariates, i.e. to test hypothesis of the form $\beta _ { \text{l} } = 0$ for one or more given values of $\operatorname{l}$, $1 \leq 1 \leq p$. Such tests include likelihood-ratio tests derived from the partial likelihood (cf. also [[Likelihood-ratio test|Likelihood-ratio test]]), or Wald test statistics based on the asymptotic normality of $\widehat { \beta }$. A thorough discussion of the tests in particular and of the Cox regression model in general is contained in [[#References|[a2]]], Sect. VII.2; [[#References|[a2]]], Sect. VII.3, presents methods for checking the proportional hazards structure assumed in (a2). |
| − | Refinements of the model (a2) include models for handling e.g. stratified data, Markov chains with regression structures for the transition intensities, etc. It should be emphasized that these models, including (a2), are only partially specified in the sense that with (a2) alone nothing much is said about the distributions of the | + | Refinements of the model (a2) include models for handling e.g. stratified data, Markov chains with regression structures for the transition intensities, etc. It should be emphasized that these models, including (a2), are only partially specified in the sense that with (a2) alone nothing much is said about the distributions of the $Z _ { k }$ or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130250/c13025074.png"/>. This, in particular, makes it extremely difficult to use the models for, e.g., the prediction of survival times. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> O.O. Aalen, "Nonparametric inference for a family of counting processes" ''Ann. Statist.'' , '''6''' (1978) pp. 701–726</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> P.K.A. Andersen, Ø. Borgan, R.D. Gill, N. Keiding, "Statistical models based on counting processes" , Springer (1993)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> P.K.A. Andersen, R.D. Gill, "Cox's regression model for counting processes: A large sample study" ''Ann. Statist.'' , '''10''' (1982) pp. 1100–1120</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> D.R. Cox, "Regression models and life-tables (with discussion)" ''J. Royal Statist. Soc. B'' , '''34''' (1972) pp. 187–220</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> D.R. Cox, "Partial likelihood" ''Biometrika'' , '''62''' (1975) pp. 269–276</td></tr></table> |
Revision as of 17:03, 1 July 2020
A regression model introduced by D.R. Cox [a4] and subsequently proved to be one of the most useful and versatile statistical models, in particular with regards to applications in survival analysis (cf. also Regression analysis).
Let $X _ { 1 } , \ldots , X _ { n }$ be stochastically independent, strictly positive random variables (cf. also Random variable), to be thought of as the failure times of $n$ different items, such that $X _ { k }$ has hazard function 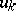 (i.e.
(i.e.
\begin{equation*} \mathsf{P} ( X _ { k } > t ) = \operatorname { exp } \left( - \int _ { 0 } ^ { t } u _ { k } ( s ) d s \right) \end{equation*}
for $t \geq 0$) of the form
\begin{equation*} u _ { k } ( t ) = \alpha ( t ) e ^ { z _ { k } ^ { T } ( t ) \beta }. \end{equation*}
Here, $\alpha$ is an unknown hazard function, the baseline hazard obtained if $\beta = 0$, and $\beta ^ { T } = ( \beta _ { 1 } , \dots , \beta _ { p } )$ is a vector of $p$ unknown regression parameters. The $z _ { k } ^ { T } ( t ) = ( z _ { k , 1 } ( t ) , \dots , z _ { k , p } ( t ) )$ denote known non-random vectors of possibly time-dependent covariates, e.g. individual characteristics of a patient referring to age, sex, method of treatment as well as physiological and other measurements.
The parameter vector $\beta$ is estimated by maximizing the partial likelihood [a5]
\begin{equation} \tag{a1} C ( \beta ) = \prod _ { j = 1 } ^ { n } \frac { \operatorname { exp } ( z _ { j } ^ { T } ( T _ { j } ) \beta ) } { \sum _ { k \in R _ { j } } \operatorname { exp } ( z _ { k } ^ { T } ( T _ { j } ) \beta ) }, \end{equation}
where $T _ { 1 } < \ldots < T _ { n }$ are the $X _ { k }$ ordered according to size, $Y _ { j } = i$ if it is item $i$ that fails at time $T _ { j }$, and $R _ { j } = \{ k : X _ { k } \geq T _ { j } \}$ denotes the set of items $k$ still at risk, i.e. not yet failed, immediately before $T _ { j }$. With this setup, the $j$th factor in $C ( \beta )$ describes the conditional distribution of $Y_{j}$ given $T _ { 1 } , \dots , T _ { j }$ and $Y _ { 1 } , \dots , Y _ { j - 1 }$.
For many applications it is natural to allow for, e.g., censorings (cf. also Errors, theory of) or truncations (the removal of an item from observation through other causes than failure) as well as random covariate processes $Z _ { k } ( t )$. Formally this may be done by introducing the counting processes $N _ { k } ( t ) = 1 _ { ( X _ { k } \leq t ,\, I _ { k } ( X _ { k } ) = 1 ) }$ registering the failures if they are observed, where 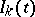 is a $0 - 1$-valued stochastic process with $I _ { k } ( t ) = 1$ if item $k$ is at risk (under observation) just before time $t$. If $\mathcal{F} _ { t }$ denotes the $\sigma$-algebra for everything observed (failures, censorings, covariate values, etc.) on the time interval $[ 0 , t ]$, it is then required that $N _ { k }$ have $\mathcal{F} _ { t }$-intensity process
is a $0 - 1$-valued stochastic process with $I _ { k } ( t ) = 1$ if item $k$ is at risk (under observation) just before time $t$. If $\mathcal{F} _ { t }$ denotes the $\sigma$-algebra for everything observed (failures, censorings, covariate values, etc.) on the time interval $[ 0 , t ]$, it is then required that $N _ { k }$ have $\mathcal{F} _ { t }$-intensity process
\begin{equation} \tag{a2} \lambda _ { k } ( t ) = \alpha ( t ) e ^ { Z _ { k } ^ { T } ( t ) \beta } I _ { k } ( t ), \end{equation}
i.e. $N _ { k } ( t ) - \int _ { 0 } ^ { t } \lambda _ { k } ( s ) d s$ defines a $\mathcal{F} _ { t }$-martingale (cf. also Martingale), while intuitively, for small $h > 0$, the conditional probability given the past that item $k$ will fail during the interval $] t , t + h ]$ is approximately $h \alpha ( t ) e ^ { Z _ { k } ^ { T } ( t ) \beta }$, provided $k$ is at risk at time $t$. For $\beta$ known, (a2) is then an example of Aalen's multiplicative intensity model [a1] with the integrated baseline hazard $A ( t ) = \int _ { 0 } ^ { t } \alpha ( s ) d s$ estimated by, for any $t$,
\begin{equation} \tag{a3} \hat { A } ( t | \beta ) = \int _ { ]0 , t] } \frac { 1 } { \sum _ { k = 1 } ^ { n } I _ { k } ( s - ) e ^ { Z _ { k } ^ { T } ( s - ) \beta } } d \overline { N } ( s ), \end{equation}
writing $\overline { N } = \sum _ { k } N _ { k }$ and where $s-$ signifies that it is the values of 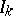 and $Z _ { k }$ just before the observed failure times that should be used. Since in practice $\beta$ is unknown, in (a3) one of course has to replace $\beta$ by the estimator $\widehat { \beta }$, still obtained maximizing the partial likelihood (a1), replacing $n$ by the random number of observed failures, replacing
and $Z _ { k }$ just before the observed failure times that should be used. Since in practice $\beta$ is unknown, in (a3) one of course has to replace $\beta$ by the estimator $\widehat { \beta }$, still obtained maximizing the partial likelihood (a1), replacing $n$ by the random number of observed failures, replacing 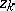 by $Z _ { k }$, and using $R _ { j } = \{ k : I _ { k } ( T _ { j } - ) = 1 \}$ with $T _ { j }$ now the $j$th observed failure. (Note that in contrast to the situation with non-random covariates described above, there is no longer an interpretation of the factors in $C ( \beta )$ as conditional distributions.)
by $Z _ { k }$, and using $R _ { j } = \{ k : I _ { k } ( T _ { j } - ) = 1 \}$ with $T _ { j }$ now the $j$th observed failure. (Note that in contrast to the situation with non-random covariates described above, there is no longer an interpretation of the factors in $C ( \beta )$ as conditional distributions.)
Using central limit theorems for martingales (cf. also Central limit theorem: Martingale), conditions may be given for consistency and asymptotic normality of the estimators $\widehat { \beta }$ and $\widehat { A } ( t | \widehat { \beta } )$, see [a3].
It is of particular interest to be able to test for the effect of one or more covariates, i.e. to test hypothesis of the form $\beta _ { \text{l} } = 0$ for one or more given values of $\operatorname{l}$, $1 \leq 1 \leq p$. Such tests include likelihood-ratio tests derived from the partial likelihood (cf. also Likelihood-ratio test), or Wald test statistics based on the asymptotic normality of $\widehat { \beta }$. A thorough discussion of the tests in particular and of the Cox regression model in general is contained in [a2], Sect. VII.2; [a2], Sect. VII.3, presents methods for checking the proportional hazards structure assumed in (a2).
Refinements of the model (a2) include models for handling e.g. stratified data, Markov chains with regression structures for the transition intensities, etc. It should be emphasized that these models, including (a2), are only partially specified in the sense that with (a2) alone nothing much is said about the distributions of the $Z _ { k }$ or 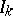 . This, in particular, makes it extremely difficult to use the models for, e.g., the prediction of survival times.
. This, in particular, makes it extremely difficult to use the models for, e.g., the prediction of survival times.
References
| [a1] | O.O. Aalen, "Nonparametric inference for a family of counting processes" Ann. Statist. , 6 (1978) pp. 701–726 |
| [a2] | P.K.A. Andersen, Ø. Borgan, R.D. Gill, N. Keiding, "Statistical models based on counting processes" , Springer (1993) |
| [a3] | P.K.A. Andersen, R.D. Gill, "Cox's regression model for counting processes: A large sample study" Ann. Statist. , 10 (1982) pp. 1100–1120 |
| [a4] | D.R. Cox, "Regression models and life-tables (with discussion)" J. Royal Statist. Soc. B , 34 (1972) pp. 187–220 |
| [a5] | D.R. Cox, "Partial likelihood" Biometrika , 62 (1975) pp. 269–276 |
Cox regression model. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cox_regression_model&oldid=50497