Convex function (of a real variable)
A function 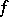 , defined on some interval, satisfying the condition
, defined on some interval, satisfying the condition
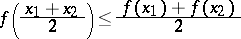 | (1) |
for every two points 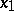 and
and 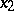 from this interval. The geometrical meaning of this condition is that the midpoint of any chord of the graph of the function
from this interval. The geometrical meaning of this condition is that the midpoint of any chord of the graph of the function 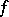 is located either above the graph or on it. If the inequality (1) is strict for all
is located either above the graph or on it. If the inequality (1) is strict for all  and
and 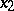 , then
, then 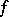 is called strictly convex. Examples of convex functions include
is called strictly convex. Examples of convex functions include 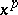 ,
, 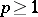 ,
, 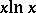 for
for 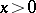 , and
, and 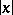 for all
for all  . If the sign of inequality (1) is reversed, the function is called concave. All measurable convex functions on open intervals are continuous. There exist convex functions which are not continuous, but they are very irregular: If a function
. If the sign of inequality (1) is reversed, the function is called concave. All measurable convex functions on open intervals are continuous. There exist convex functions which are not continuous, but they are very irregular: If a function 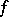 is convex on the interval
is convex on the interval  and is bounded from above on some interval lying inside
and is bounded from above on some interval lying inside 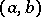 , it is continuous on
, it is continuous on  . Thus, a discontinuous convex function is unbounded on any interior interval and is not measurable.
. Thus, a discontinuous convex function is unbounded on any interior interval and is not measurable.
If a function 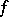 is continuous on an interval, and if each chord of its graph contains at least one point other than the end points of the chord and lying above the graph or on it,
is continuous on an interval, and if each chord of its graph contains at least one point other than the end points of the chord and lying above the graph or on it, 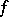 is convex. It follows from condition (1) that for a continuous function the centre of gravity of any finite number of material points lying on the graph of the function lies either above the graph or on it: For any numbers
is convex. It follows from condition (1) that for a continuous function the centre of gravity of any finite number of material points lying on the graph of the function lies either above the graph or on it: For any numbers 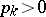 ,
, 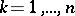 (where
(where  is arbitrary), the Jensen inequality
is arbitrary), the Jensen inequality
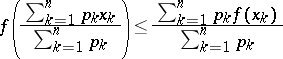 | (2) |
is valid.
If, for some function 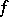 , inequality (2) is true for any two points
, inequality (2) is true for any two points 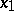 and
and 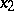 in some interval and any
in some interval and any 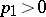 and
and 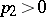 , the function
, the function 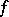 is continuous and, of course, convex on this interval. Any chord of the graph of a continuous convex function coincides with the corresponding part of the graph or lies entirely above the graph except for its end points. This means that if a continuous convex function is not linear on any interval, strict inequality is realized in (1) and (2) for any pairwise different values of the argument, i.e.
is continuous and, of course, convex on this interval. Any chord of the graph of a continuous convex function coincides with the corresponding part of the graph or lies entirely above the graph except for its end points. This means that if a continuous convex function is not linear on any interval, strict inequality is realized in (1) and (2) for any pairwise different values of the argument, i.e. 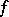 is a strictly convex function.
is a strictly convex function.
A continuous function is convex if and only if the set of points of the plane located above its graph, i.e. its supergraph, is a convex set. For a continuous function 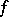 , defined on an interval
, defined on an interval 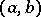 , to be convex, it is necessary and sufficient that for each point on the graph there be at least one straight line (known as a supporting line) situated under the graph (on the interval
, to be convex, it is necessary and sufficient that for each point on the graph there be at least one straight line (known as a supporting line) situated under the graph (on the interval 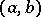 ) or partly on the graph that passes through the point, i.e. for any point
) or partly on the graph that passes through the point, i.e. for any point 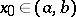 there exists a
there exists a 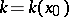 such that
such that
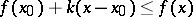 | (3) |
for all 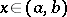 .
.
A continuous function which is convex on an open interval has no strict local maximum. If a function 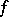 is continuous and convex on an interval
is continuous and convex on an interval 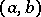 , it has, at each one of its points
, it has, at each one of its points 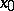 , a finite left,
, a finite left, 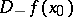 , and right,
, and right, 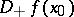 , derivative; moreover,
, derivative; moreover, 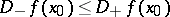 and, in addition, if the number
and, in addition, if the number 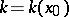 satisfies condition (3), the inequalities
satisfies condition (3), the inequalities 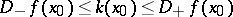 hold. The functions
hold. The functions 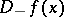 and
and 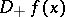 do not decrease, and at all points except, possibly, a countable number of them,
do not decrease, and at all points except, possibly, a countable number of them, 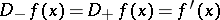 , so that
, so that 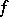 is differentiable at these points. On each closed interval located inside
is differentiable at these points. On each closed interval located inside 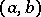 the function
the function 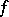 satisfies a Lipschitz condition and is thus absolutely continuous. This makes it possible to establish the following convexity criterion: A continuous function is convex if and only if it is the indefinite integral of a non-decreasing function.
satisfies a Lipschitz condition and is thus absolutely continuous. This makes it possible to establish the following convexity criterion: A continuous function is convex if and only if it is the indefinite integral of a non-decreasing function.
If a function 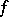 is differentiable on an interval, it is (strictly) convex on this interval if and only if its derivative does not decrease (is increasing). At a point of the graph of a continuous convex function at which the function is differentiable there exists a unique supporting line — the tangent at this point. On the other hand, if, at any point of the graph of a function which is differentiable on an interval, the tangent to the graph at that point lies under the graph in some neighbourhood of that point (except at the tangency point itself), the function is strictly convex; if it lies under the graph or partly on it, it is just a convex function.
is differentiable on an interval, it is (strictly) convex on this interval if and only if its derivative does not decrease (is increasing). At a point of the graph of a continuous convex function at which the function is differentiable there exists a unique supporting line — the tangent at this point. On the other hand, if, at any point of the graph of a function which is differentiable on an interval, the tangent to the graph at that point lies under the graph in some neighbourhood of that point (except at the tangency point itself), the function is strictly convex; if it lies under the graph or partly on it, it is just a convex function.
If the function 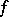 is twice-differentiable on the interval, it is convex on this interval if and only if its second derivative is non-negative on this interval (this theorem is valid for the second symmetric derivative, as well as for the ordinary second derivative). If the function has a positive second derivative at each point of some interval, it is strictly convex on that interval.
is twice-differentiable on the interval, it is convex on this interval if and only if its second derivative is non-negative on this interval (this theorem is valid for the second symmetric derivative, as well as for the ordinary second derivative). If the function has a positive second derivative at each point of some interval, it is strictly convex on that interval.
If the functions 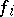 are convex on an interval
are convex on an interval 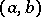 and
and  ,
, 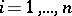 , then the function
, then the function
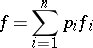 |
is also convex on this interval; also, if even one of the functions 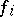 is strictly convex,
is strictly convex, 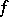 is strictly convex as well.
is strictly convex as well.
There exist various generalizations of the concept of convexity to functions of several variables. For instance, let a function 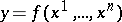 be defined on a convex set
be defined on a convex set 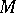 of the
of the  -dimensional affine space
-dimensional affine space 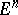 . The function
. The function 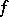 is called convex if inequality (1) is valid for all points
is called convex if inequality (1) is valid for all points 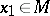 and
and 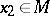 , where
, where 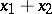 denotes the sum of the
denotes the sum of the  -dimensional vectors
-dimensional vectors 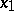 and
and  . The properties of a convex function of one variable are correspondingly generalized to functions of several variables; for example, inequality (2) is satisfied only for continuous convex functions. A continuous function is convex if and only if the set of points
. The properties of a convex function of one variable are correspondingly generalized to functions of several variables; for example, inequality (2) is satisfied only for continuous convex functions. A continuous function is convex if and only if the set of points 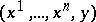 of the space
of the space 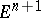 lying above its graph is convex.
lying above its graph is convex.
A continuous function 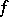 defined on a convex domain
defined on a convex domain 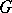 is convex if and only if for each point
is convex if and only if for each point 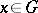 there exists a linear function
there exists a linear function
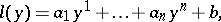 |
such that
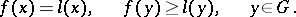 | (4) |
The hyperplane defined by the equation 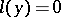 is called a supporting hyperplane.
is called a supporting hyperplane.
If a function  is continuously differentiable in
is continuously differentiable in 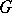 , condition (4) is equivalent to the condition
, condition (4) is equivalent to the condition
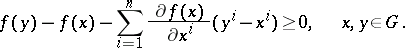 |
If 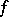 is twice-differentiable, condition (4) is equivalent to the condition that the second differential of the function, i.e. the quadratic form
is twice-differentiable, condition (4) is equivalent to the condition that the second differential of the function, i.e. the quadratic form
 |
is non-negative for all 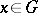 .
.
Another important generalization of the concept of a convex function for functions of several variables is the concept of a subharmonic function. The concept of a convex function can be extended in a natural manner to include functions defined on corresponding subsets of infinite-dimensional linear spaces; cf. Convex functional.
References
| [1] | N. Bourbaki, "Elements of mathematics. Functions of a real variable" , Addison-Wesley (1976) pp. Chapt. 1 Sect. 4 (Translated from French) |
| [2] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) pp. Chapt. 1 |
| [3] | L.D. Kudryavtsev, "Mathematical analysis" , 1 , Moscow (1973) pp. Chapt. 1 (In Russian) |
| [4] | I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , Deutsch. Verlag Wissenschaft. , Frankfurt a.M. (1961) pp. Chapt. 10 (Translated from Russian) |
| [5] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) pp. Chapt. 5 (Translated from Russian) |
| [6] | G.H. Hardy, J.E. Littlewood, G. Pólya, "Inequalities" , Cambridge Univ. Press (1934) pp. Chapt. 3 |
Comments
Convexity of a real-valued function 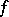 on an interval
on an interval 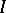 is often defined by the condition that
is often defined by the condition that
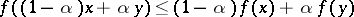 | (*) |
whenever 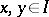 and
and 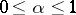 . This implies that
. This implies that 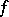 is continuous on the interior of
is continuous on the interior of 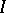 . For measurable
. For measurable  , (1) and (*) are equivalent. A function
, (1) and (*) are equivalent. A function  satisfying (1) is also called midpoint convex.
satisfying (1) is also called midpoint convex.
References
| [a1] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) pp. 199–206; 334 |
| [a2] | V. Barbu, Th. Precupanu, "Convexity and optimization in Banach spaces" , Reidel (1986) pp. Chapt. 2 |
Convex function (of a real variable). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convex_function_(of_a_real_variable)&oldid=15815